Exercise 6.3(Linear Inequalities)
Solve the following system of inequalities graphically:(Ex 6.3 Linear Inequalities ncert math solution class 11)
Question 1: x ≥ 3, y ≥ 2
Solution : Given that, x ≥ 3 …..(i)
y ≥ 2…….(ii)
The graph of the lines x = 3 and y = 2 are drawn in the figure below.
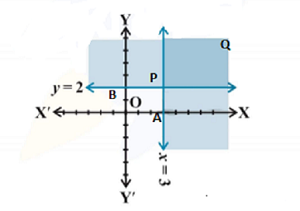
The common shaded region is the solution of given system of linear inequalities
Question 2: 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solution : Given that,
3x + 2y ≤ 12 –(i)
x ≥ 1 –(ii)
x ≥ 2 –(iii)
Taking (i) eqation
3x + 2 y =12
![]()
The graph of the lines 3x + 2 y =12, x = 1 and y = 2 are drawn in the figure below.
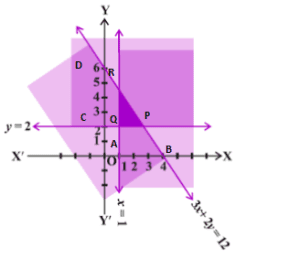
The common shaded region ΔPQR is the solution of given system of linear inequalities
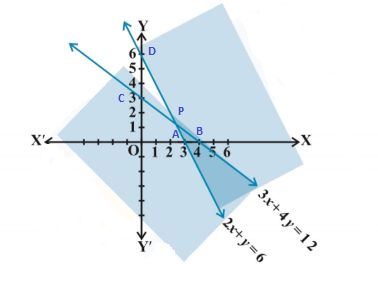
Question 3: 2x + y ≥ 6, 3x + 4y ≤ 12
Solution: Given that, 2x + y ≥ 6…………… (i)
3x + 4y ≤ 12 ……………. (ii)
Taking eqation (i)
2x + y = 6
![]()
Taking equation (ii)
3x + 4y = 12
![]()
The graph of the lines 2x + y = 6 and 3x + 4y = 12 are drawn in the figure below
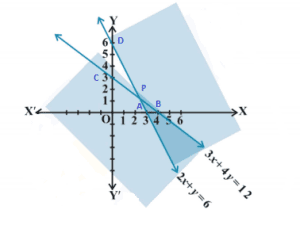
The common shaded region is the solution of given system of linear inequalities
Question 4: x + y ≥ 4, 2x – y < 0
Solution : Given that, x + y ≥ 4 —(i)
2x – y < 0 —(ii)
Taking eqation (i)
x + y = 4
![]()
Taking equation (ii)
2x – y = 0
![]()
The graph of the lines x + y = 4 and 2x – y = 0 are drawn in the figure below
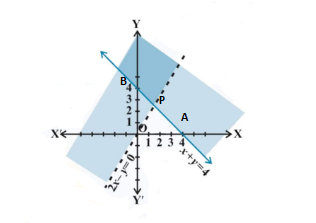
The common shaded region is the solution of given system of linear inequalities
Question 5: 2x – y >1, x – 2y < – 1
Solution: Given that : 2x – y >1…… (i)
x – 2y < – 1…….(ii)
Taking equation (i)
2x – y = 1
![]()
Taking equation (ii)
x – 2y = – 1…….(ii)
![]()
The graph of the lines 2x – y = 1 and x – 2y = – 1 are drawn in the figure below
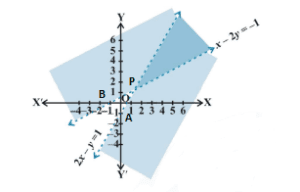
The common shaded region is the solution of given system of linear inequalities
Question 6: x + y ≤ 6, x + y ≥ 4
Solution: Given that,
x + y ≤ 6….(i)
x + y ≥ 4……(ii)
Taking equation (i)
x + y = 6
![]()
Taking equation (ii)
x + y = 4
![]()
The graph of the lines x + y = 6 and x + y = 4 are drawn in the figure below
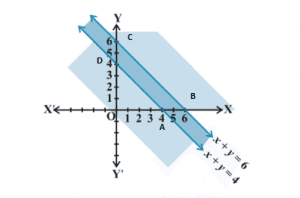
The common shaded region ABCD is the solution of given system of linear inequalities
Question 7: 2x + y ≥ 8, x + 2y ≥ 10
Solution: Given that,
2x + y ≥ 8 ….(i)
x + 2y ≥ 10 …..(ii)
Taking equation (i)
2x + y = 8
![]()
Taking equation (ii)
x + 2y = 10
![]()
The graph of the lines 2x + y = 8 and x + 2y = 10 are drawn in the figure below

The common shaded region is the solution of given system of linear inequalities
Question 8: x + y ≤ 9, y > x, x ≥ 0
Solution: Given that,
x + y ≤ 9 …..(i)
y > x ….(ii)
x ≥ 0 …(iii)
Taking equation (i)
x + y = 9
![]()
Taking equation (ii)
y = x
![]()
The graph of the lines x + y = 9, y = x and x = 0 are drawn in the figure below:

The common shaded region is the solution of given system of linear inequalities
Question 9: 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solution: Given that,
5x + 4y ≤ 20 ….(i)
x ≥ 1 ……(ii)
y ≥ 2 ……(iii)
Taking equation (i)
5x + 4y = 20 …..(i)
![]()
The graph of the lines 5x + 4y = 20, x = 1 and y = 2 are drawn in the figure below:
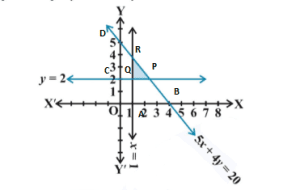
The common shaded region ΔPQR is the solution of given system of linear inequalities
Question 10: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solution: Given that,
3x + 4y ≤ 60 …..(i)
x + 3y ≤ 30 ……(ii)
Taking equation (i)
3x + 4y = 60
![]()
Taking equation (ii)
x + 3y = 30
![]()
The graph of the lines 3x + 4y = 60 and x + 3y = 30 are drawn in the figure below:

The common shaded region OAPC is the solution of given system of linear inequalities
Question 11: 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Solution : Given that,
2x + y = 4 …..(i)
x + y ≤ 3 …….(ii)
2x – 3y ≤ 6 …..(iii)
Taking equation (i)
2x + y = 4
![]()
Taking equation (ii)
x + y = 3
![]()
2x – 3y = 6
![]()
The graph of the lines 2x + y = 4, x + y = 3 and 2x – 3y = 6 are drawn in the figure below:
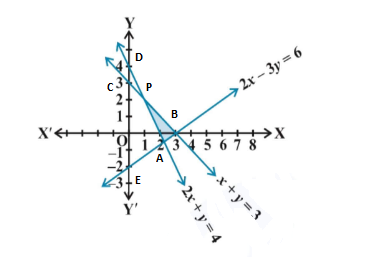
The common shaded region ΔABP is the solution of given system of linear inequalities
Question 12: x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0 , y ≥ 1
Solution : Given that,
x – 2y ≤ 3 …..(i)
3x + 4y ≥ 12 ……(ii)
y ≥ 1 …..(iii)
Taking equation (i)
x – 2y = 3
![]()
Taking equation (ii)
3x + 4y = 12
![]()
The graph of the lines x – 2y = 3, 3x + 4y = 12 and y = 1 are drawn in the figure below:

The common shaded region is the solution of given system of linear inequalities
Question 13: 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Solution : Given that,
4x + 3y = 60 …….(i)
y = 2x …….(ii)
x = 3 …….(iii)
Taking equation (i)
4x + 3y = 60
![]()
Taking equation (ii)
y = 2x
![]()
The graph of the lines 4x + 3y = 60, y = 2x and x = 3 are drawn in the figure below:
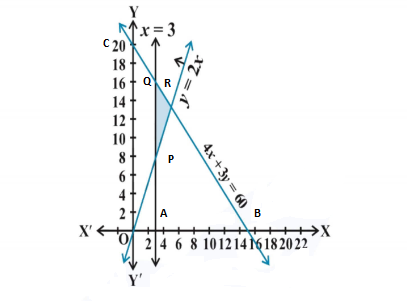
The common shaded region ΔPQR is the solution of given system of linear inequalities.
Question 14: 3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0, x ≥ 0
Solution : Given that,
3x + 2y ≤ 150 …(i)
x + 4y ≤ 80 …..(ii)
x ≤ 15 ….(iii)
Taking equation (i)
3x + 2y = 150
![]()
Taking equation (ii)
x + 4y = 80
![]()
The graph of the lines 3x + 2y = 150 , x + 4y = 80 and x = 15 are drawn in the figure below:
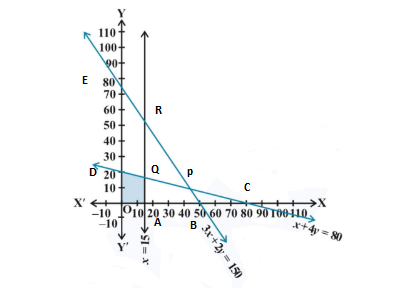
The common shaded region OAQD is the solution of given system of linear inequalities.
Question 15: x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Solution : Given that:
x + 2y ≤ 10 …..(i)
x + y ≥ 1 …….(ii)
x – y ≤ 0 …….(iii)
Taking equaation (i)
x + 2y = 10
![]()
Taking equation (ii)
x + y = 1
![]()
Taking equation (iii)
x – y = 0
![]()
The graph of the lines x + 2y = 10 , x + y = 1 and x – y = 0 are drawn in the figure below:
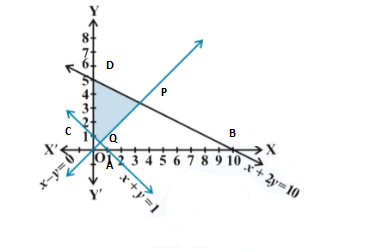
The common shaded region CQPD is the solution of given system of linear inequalities.
Ex 6.1 Linear Inequalities ncert math solution class 11
Ex 6.2 Linear Inequalities ncert math solution class 11
Ex 6.3 Linear Inequalities ncert math solution class 11