Case study inverse trigonometry 2 chapter 2 class 12

by

Case study Chapter 2 (Inverse Trigonometry)

Case study 2:- Read the following and answer the question.(Case study inverse trigonometry 1)

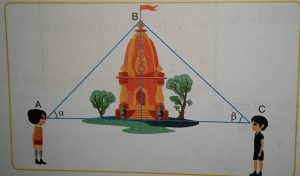
Case study inverse trigonometry 2
Two men on either side of a temple 30 metres high observes

  Two men on either side of a temple 30 metres high observes its top at the angles of elevation α and β respectively. (as shown in the figure above). the distance between the two men is 40√3 metres and the distance between the first person A and the temple is 30√3 metres.

(i) ∠CAB = α =

(a) \sin^{-1}\frac{2}{\sqrt{3}}     (b)  \sin^{-1}\frac{1}{2}

(c) \sin^{-1}2                             (d) \sin^{-1}\frac{\sqrt{3}}{2}

(ii) ∠CAB = α =

(a) \cos^{-1}(\frac{1}{5})                 (b) \cos^{-1}(\frac{2}{5})

(c) \cos^{-1}\frac{\sqrt{3}}{2}         (d) \cos^{-1}(\frac{4}{5})

(iii) ∠BCA = β = 

(a) \tan^{-1}(\frac{1}{2})            (b) \tan^{-1}2

(c) \tan^{-1}(\frac{1}{\sqrt{3}})             (d) tan^{-1}\sqrt{3}

(iv) ∠ABC = 

(a) π/4                       (b) π/6

(c) π/2                         (d) π/3

(v) Domain and range of \cos^{-1}x are respectively

(a) (-1, 1), (0, π)                (b) [-1, 1], (0, π)

(c) [-1, 1], [0, π]                 (d) (-1, 1), [-π/2, π/2]

Solution :We have

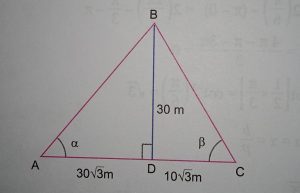
(i) Answer (b)

Now in ΔABD (right angled)

\tan\alpha =\frac{BD}{AD}= \frac{30}{30\sqrt{3}} = \frac{1}{sqrt{3}}

\Rightarrow \tan\alpha = \tan 30^{\circ}

\Rightarrow \alpha = 30^{\circ}

\Rightarrow \sin \alpha = \sin 30 = \frac{1}{2}

\Rightarrow \alpha =\sin^{-1}(\frac{1}{2})

(ii) Answer (c) 

We have from (i)

\alpha = 30^{\circ}

\Rightarrow \cos\alpha = \cos 30 = \frac{\sqrt{3}}{2}

\Rightarrow \alpha = \cos^{-1}(\frac{\sqrt{3}}{2}

(iii) Answer (d)

In right ΔBCD, we have

\tan\bete = \frac{BD}{DC}

\Rightarrow \tan\beta = \frac{30}{10\sqrt{3}}=\frac{3}{\sqrt{3}}=\sqrt{3}

\Rightarrow \beta = \tan^{-1}(\sqrt{3})

(iv) Answer (c)

ΔABC, we have,

∠ABC + ∠BAC  +  ∠ACB = 180°

⇒  ∠ABC + α + β = 180°

⇒  ∠ABC + 30 + 60 = 180

⇒  ∠ABC = 90

⇒  ∠ABC = π/2

(v) Answer (c)

Let

\cos^{-1}x = y \Rightarrow x =\cos y

-1\leq \cos y\leq 1 \Rightarrow -1\leq x \leq 1

Domain =[-1, 1]

0\leq y \leq \pi

Range = [0, π]

Some other Case study problem

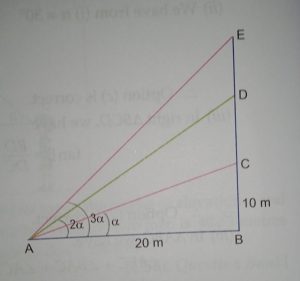
Case study 1:-  The government of India is planning to fix a hoarding board at the face of a building on yhe road of bisy market for awaeeness on COVID-19 protocol. Ram , Robert and Rahim are the three engineers who are working on this project. “A” is considered to be person viewing the hoarding board 20 metres away from the building , standing at the edge of a pathwaynearby . Ram , Robert and Rahim suggested to the firm to place the hoarding board at three different locations namely C, D and E. “C” is at the height of  10 metres from the ground level. for the viewer A, the angle of elevation of “D” is double the angle of elevation of “C” the angle of elevation of “E” is triple the angle of elevation of “C” for the same viewer.(Case study inverse trigonometric 1 )

Solution: For solution click here

Case study problem matrix 2
Amit, Biraj and chirag were giventhe task of creating a square matrix of order 2

Case study problem determinant 1

Case study application of derivative 1
A recangular hall is to be developed for a meeting of farmers in an agriculture college to aware

Leave a Comment