Case study Chapter 10 (Vectors)
Solar panels have to be installed carefully so that the tilt of the roof, and the direction to the sun , produce the largest possible electrical power in the solar panals.(Case study problem vector 1)
A surveyor uses his instrument to determine the co-ordinates of the four corners of a roof where solar panels are to
be mounted. In the picture, suppose the points are labelled counter clockwise from the roof corner nearest to the
camera in units of meters ![]() and
and ![]() .
.
Based on the above information answer the following question.
(i) Find the components to the two edge vectors defined by ![]() and
and ![]() ?
?
(ii) (a) Find the magnitudes of the vectors ![]() and
and ![]() .
.
(b) Find the components to the vectors ![]() , perpendicular to
, perpendicular to ![]() and
and ![]() and the surface of the roof.
and the surface of the roof.
Solution: Given points are ![]() and
and ![]() .
.
(i) We have,
![]()
![]()
![]()
Components of vector A are ![]()
and ![]()
![]()
![]()
Components of vector B are ![]() .
.
(ii) (a) We have
![]() units
units
![]() units
units
(b) We have,
![]()
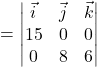
![]()
![]()
Its components are ![]()
2. Read the following and answer the question:
A class XII student appearing for a competitive examination was asked to attempt the following question.
Let ![]() and
and ![]() be three non zero vectors.
be three non zero vectors.
(i) If ![]() and
and ![]() are such that
are such that ![]()
(a) ![]() (b)
(b) ![]()
(c) ![]() (d) None of these
(d) None of these
(ii) If ![]() then evaluate
then evaluate ![]()
(a) 0 (b) 4
(c) 3 (d) 2
(iii) If ![]() and
and ![]() are unit vectors and
are unit vectors and ![]() be the angle between them then
be the angle between them then ![]() is
is
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
(iv) Let ![]() and
and ![]() be unit vectors such that
be unit vectors such that ![]() and angle
and angle
between ![]() and
and ![]() is
is ![]() then
then ![]()
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
(v) The area of parallelogram formed by ![]() and
and ![]() as
as
diagonals is
(a) 70 (b) 35
(c) ![]() (d)
(d) ![]()
Solution:(i) Answer (a)
Given, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(ii) Answer (a)
![]()
![]()
![]()
![]()
![]()
And
![]()
![]()
![]()
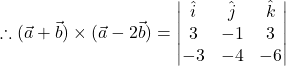
![]()
![]()
![]()
![]()
![]()
(iii) Answer(b)
Given, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
(iv) Answer (c)
We have ![]()
![]()
And ![]()
Since angle between ![]() and
and ![]() is
is ![]()
![]()
(v) Answer (c)
The area of the parallelogram formed by ![]() and
and ![]() as diagonal
as diagonal ![]()
![]()
Now, 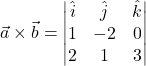
![]()
![]()
![]()
![]()
Area ![]() sq.units.
sq.units.
Some other case study question
Case study: A man is watching an aeroplane which is at the co-ordinate point A(4, -1, 3) assuming that the man is at O(0, 0, 0). At the same time he saw a bird at the coordinate point B(2, 0, 4).
Based on the above information answer the following:
(a) Find the position vector ![]()
(b) Find the distance between aeroplane and bird
(c) Find the unit vector along ![]() .
.
(d) Find the direction cosine of ![]() .
.
(e) Find the angles which ![]() makes with x, y and z axes.
makes with x, y and z axes.
Solution: For solution click here


