int root cotx + root tanx dx

by

Question:

  \displaystyle \int \left[\sqrt{\cot x}+\sqrt{\tan x}\right] dx

Solution:  Let I = \displaystyle \int \left[\sqrt{\cot x}+\sqrt{\tan x}\right] dx

=\displaystyle \int \left[\sqrt{\cot x}+\frac{1}{\sqrt{\cot x}}\right]dx

= \displaystyle \int \left[\frac{\cot x+1}{\sqrt{\cot x}}\right]dx

= \displaystyle \int \sqrt{\tan x} [\cot x+1 ]dx—–(i)

Let \tan x = t^2 \Rightarrow \cot x = \frac{1}{t^2}

differentiate with respect to x

\sec^2t = 2t\frac{dt}{dx}

\Rightarrow dx = 2t\frac{ dt}{\sec^2t}

\Rightarrow dx = \frac{2t}{1+\tan^2x}dt

\Rightarrow dx = \frac{2t}{1+t^4}dt

Putting in eq (i)

= \displaystyle \int t\left[\frac{1}{t^2}+1\right]\frac{2t}{1+t^4}dt

= \displaystyle \int \left[\frac{1+t^2}{t^2}\right]\frac{2t^2}{1+t^4}dt

=2\displaystyle \int \left[\frac{1+t^2}{1+t^4}\right]dt

Divide by t^2 in numerator and denominator

= 2\displaystyle \int \left[\frac{\frac{1}{t^2}+1}{\frac{1}{t^2}+t^2}\right]dt

= 2\displaystyle \int \left[\frac{1+\frac{1}{t^2}}{t^2+\frac{1}{t^2}}\right]dt

= 2\displaystyle \int \left[\frac{1+\frac{1}{t^2}}{t^2+\frac{1}{t^2}-2+2}\right]dt

= 2\displaystyle \int \left[\frac{1+\frac{1}{t^2}}{(t-\frac{1}{t})^2+2}\right]dt

Let t-\frac{1}{t}= y

D.w.r. t.x

\Rightarrow 1+\frac{1}{t^2} =\frac{dy}{dt}

\Rightarrow \left(1+\frac{1}{t^2}\right)dt = dy

Now

= 2\displaystyle \int \frac{1}{y^2+(\sqrt{2})^2}dt

= \frac{2}{\sqrt{2}}\tan^{-1}\frac{y}{\sqrt{2}}+C

= \sqrt{2}\tan^{-1}\frac{\left(t-\frac{1}{t}\right)}{\sqrt{2}}dt+C

= \sqrt{2}\tan^{-1}\frac{t^2-1}{\sqrt{2}t}+C

= \sqrt{2}\tan^{-}\left(\frac{\tan x-1}{\sqrt{2\tan x}}\right)+C

             OR

We can do this question with another method 

I = \displaystyle \int \left[\sqrt{\cot x}+\sqrt{\tan x}\right] dx

= \displaystyle \int \left[\sqrt{\frac {\cos x}{\sin x}}+\sqrt{\frac{\sin x}{\cos x}}\right]dx

= \displaystyle \int\left[\frac{\cos x+\sin x}{\sqrt{\sin x.\cos x}}\right]dx —(i)

Let \sin x-\cos x = t

Differentiate with respect to x

\cos x+\sin x = \frac{dt}{dx}

\Rightarrow (\cos x+\sin x)dx = dt

Again taking

\sin x - \cos x = t

Squaring both side

(\sin x -\cos x)^2=t^2

\Rightarrow \sin^2x+\cos^2x-2\sin x.\cos x = t^2

\Rightarrow 1-2\sin x.\cos x = t^2

\Rightarrow 1-t^2 =2\sin x.\cos x

\Rightarrow \sin x.\cos x = \frac{1-t^2}{2}

Putting in (i)

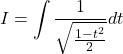
I=\displaystyle \int \frac{1}{\sqrt{\frac{1-t^2}{2}}}dt

= \sqrt{2}\displaystyle \int \frac{1}{\sqrt{1-t^2}}dt

= \sqrt{2}\sin^{-1}t+C

= \sqrt{2}\sin^{-1}(\sin x-\cos x)+C

 

 

Leave a Comment