Chapter 7:Miscellaneous Exercise

Integrate the functions in Exercises 1 to 24.(Chapter 7 Miscellaneous integration ncert maths solution class 12)

Chapter 7 Miscellaneous integration ncert maths class 12

Question 1: $\int\frac{1}{x-x^3}dx$

Solution: $\frac{1}{x-x^3}=\frac{1}{x\left(1-x^2\right)}=\frac{1}{x(1-x)(1+x)}$

Let $\frac{1}{x(1-x)(1+x)}=\frac{A}{x}+\frac{B}{(1-x)}+\frac{C}{(1+x)}--(i)$

$\Rightarrow 1=A\left(1-x^2\right)+B x(1+x)+C x(1-x)$

Let $x = 1$

$1 = 0+B(1)(1+1)+0$

$\Rightarrow 1 = 2B$

$\Rightarrow B = 1/2$

Let $x = -1$

$1 = 0+0+C((-1)(1+1)$

$\Rightarrow 1 = -2C$

$\Rightarrow C = -1/2$

Let $x = 0$

$1=A(1-0)+0+0$

$\Rightarrow A = 1$

From equation (1), we have

$\frac{1}{x(1-x)(1+x)}=\frac{1}{x}+\frac{1}{2(1-x)}-\frac{1}{2(1+x)}$

Now, $I=\int \frac{1}{x(1-x)(1+x)} d x=\int \frac{1}{x} d x+\frac{1}{2} \int \frac{1}{(1-x)} d x-\frac{1}{2} \int \frac{1}{(1+x)} d x$

$=\log |x|-\frac{1}{2} \log |(1-x)|-\frac{1}{2} \log |(1+x)|$

$=\log |x|-\log \left|(1-x)^{\frac{1}{2}}\right|-\log \left|(1+x)^{\frac{1}{2}}\right|$

$=\log \left|\frac{x}{(1-x)^{\frac{1}{2}}(1+x)^{\frac{1}{2}}}\right|+C=\log \left|\left(\frac{x^2}{1-x^2}\right)^{\frac{1}{2}}\right|+C=\frac{1}{2} \log \left|\frac{x^2}{1-x^2}\right|+C$

Question 2: $\int\frac{1}{\sqrt{x+a}+\sqrt{x+b}}dx$

Solution: let $I =\int\frac{1}{\sqrt{x+a}+\sqrt{x+b}}dx$

$=\int\frac{1}{\sqrt{x+a}+\sqrt{x+b}} \times \frac{\sqrt{x+a}-\sqrt{x+b}}{\sqrt{x+a}-\sqrt{x+b}}dx$

$=\int\frac{\sqrt{x+a}-\sqrt{x+b}}{(x+a)-(x+b)}dx$

$=\int\frac{\sqrt{x+a}-\sqrt{x+b}}{a-b}dx$

$I=\int \frac{1}{\sqrt{x+a}+\sqrt{x+b}} d x$

$=\frac{1}{a-b} \int(\sqrt{x+a}-\sqrt{x+b}) d x$

$=\frac{1}{a-b}\left[\frac{(x+a)^{\frac{3}{2}}}{\frac{3}{2}}-\frac{(x+b)^{\frac{3}{2}}}{\frac{3}{2}}\right]$

$=\frac{2}{3(a-b)}\left[(x+a)^{\frac{3}{2}}-(x+b)^{\frac{3}{2}}\right]+C$

Question 3: $\int\frac{1}{x \sqrt{a x-x^2}}dx$

Solution: $I=\int \frac{1}{x \sqrt{a x-x^2}} d x$

Let $x=\frac{a}{t} \Rightarrow d x=-\frac{a}{t^2} d t$

$I=\int \frac{1}{x \sqrt{a x-x^2}} d x$

$=\int \frac{1}{\frac{a}{t} \sqrt{a \cdot \frac{a}{t}-\left(\frac{a}{t}\right)^2}}\left(-\frac{a}{t^2} d t\right)$

$=-\int \frac{1}{a t} \cdot \frac{1}{\sqrt{\frac{1}{t}-\frac{1}{t^2}}} d t$

$=-\frac{1}{a} \int \frac{1}{\sqrt{\frac{t^2}{t}-\frac{t^2}{t^2}}} d t=-\frac{1}{a} \int \frac{1}{\sqrt{t-1}} d t=-\frac{1}{a}[2 \sqrt{t-1}]+C$

$=-\frac{1}{a}\left[2 \sqrt{\frac{a}{x}-1}\right]+C$

$=-\frac{2}{a}\left[\frac{\sqrt{a-x}}{\sqrt{x}}\right]+C$

$=-\frac{2}{a}\left[\sqrt{\frac{a-x}{x}}\right]+C$

Question 4: $\int\frac{1}{x^2\left(x^4+1\right)^{\frac{3}{4}}}dx$

Solution: Let $I=\int\frac{1}{x^2\left(x^4+1\right)^{\frac{3}{4}}}dx$

$I=\int \frac{1}{x^2\left(x^4+1\right)^{\frac{3}{4}}} d x$

$=\int \frac{1}{x^2(x^4)^{3/4}\left(1+\frac{1}{x^4}\right)^{\frac{3}{4}}} d x$

$=\int \frac{1}{x^5}(1+\frac{1}{x^4})^{-3/4}dx$

$\text { Let }1+ \frac{1}{x^4}=t$

$\Rightarrow-\frac{4}{x^5} d x=d t$

$\Rightarrow \frac{1}{x^5} d x=-\frac{d t}{4}$

$I=-\frac{1}{4} \int(t)^{-\frac{3}{4}} d t$

$=-\frac{1}{4}\left[\frac{(t)^{\frac{1}{4}}}{\frac{1}{4}}\right]+C$

$=-\frac{1}{4} \frac{\left(1+\frac{1}{x^4}\right)^{\frac{1}{4}}}{\frac{1}{4}}+C$

$=-\left(1+\frac{1}{x^4}\right)^{\frac{1}{4}}+C$

Question 5: $\int\frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}dx \quad\left[\text { Hint } \frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}=\frac{1}{x^{\frac{1}{3}}\left(1+x^{\left.\frac{1}{6}\right)}\right.} \quad \text { Put } x=t^6\right]$

Solution: Let $I= \int \frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}dx$

$=\int \frac{1}{x^{\frac{1}{3}}\left(1+x^{\frac{1}{6}}\right)}dx$

Let $x=t^6 \Rightarrow d x=6 t^5 d t$

$I=\int \frac{6 t^5}{t^2(1+t)} d t$

$=6 \int \frac{ t^3}{(1+t)} d t$

Dividing $t^3$ by denominator $1+t$ , we have

$I=6 \int\left\{\left(t^2-t+1\right)-\frac{1}{1+t}\right\} d t$

$=6\left[\left(\frac{t^3}{3}\right)-\left(\frac{t^2}{2}\right)+t-\log |1+t|\right]$

$=2 x^{\frac{1}{2}}-3 x^{\frac{1}{3}}+6 x^{\frac{1}{6}}-6 \log \left(1+x^{\frac{1}{6}}\right)+C$

$=2 \sqrt{2}-3 x^{\frac{1}{3}}+6 x^{\frac{1}{6}}-6 \log \left(1+x^{\frac{1}{6}}\right)+C$

Question 6: $\int\frac{5 x}{(x+1)\left(x^2+9\right)}dx$

Solution: Let $\frac{5 x}{(x+1)\left(x^2+9\right)}=\frac{A}{(x+1)}+\frac{B x+C}{\left(x^2+9\right)}--(i)$

$\Rightarrow 5 x=A\left(x^2+9\right)+(B x+C)(x+1)$

Let $x = -1$

$5\times -1=A((-1)^2+9)+0$

$\Rightarrow -5 = 10A$

$\Rightarrow A = -1/2$

Let $x=0$

$0 = A(0+9)+(0+C)(0+1)$

$\Rightarrow 0 = 9A +C$

$\Rightarrow C =-9A$

$\Rightarrow C =\frac{9}{2}$

Let $x =1$

$5\times 1= A(1+9)+(B+C)(1+1)$

$\Rightarrow 5 =10A+2B+2C$

$\Rightarrow 5 =10\times -\frac{1}{2}+2B+2C\times\frac{9}{2}$

$\Rightarrow 5 = -5 +2B+9$

$\Rightarrow B=1/2$

From equation (1), we have

$\frac{5 x}{(x+1)\left(x^2+9\right)}=\frac{-1}{2(x+1)}+\frac{\frac{x}{2}+\frac{9}{2}}{\left(x^2+9\right)}$

$\text { Now, } I=\int \frac{5 x}{(x+1)\left(x^2+9\right)} d x=\int\left\{\frac{-1}{2(x+1)}+\frac{(x+9)}{2\left(x^2+9\right)}\right\} d x$

$=-\frac{1}{2} \log |x+1|+\frac{1}{2} \int \frac{x}{\left(x^2+9\right)} d x+\frac{9}{2} \int \frac{1}{\left(x^2+9\right)} d x$

$=-\frac{1}{2} \log |x+1|+\frac{1}{4} \int \frac{2 x}{\left(x^2+9\right)} d x+\frac{9}{2} \int \frac{1}{\left(x^2+9\right)} d x$

$=-\frac{1}{2} \log |x+1|+\frac{1}{4} \log \left|x^2+9\right|+\frac{9}{2} \cdot \frac{1}{3} \tan ^{-1} \frac{x}{3}+C$

$=-\frac{1}{2} \log |x+1|+\frac{1}{4} \log \left(x^2+9\right)+\frac{3}{2} \tan ^{-1} \frac{x}{3}+C$

Question 7: $\int \frac{\sin x}{\sin (x-a)}dx$

Solution: Let $I=\int \frac{\sin x}{\sin (x-a)} d x$

Let $(x-a)=t \Rightarrow d x=d t$

$I=\int \frac{\sin x}{\sin (x-a)} d x$

$=\int \frac{\sin (t+a)}{\sin t} d t$

$=\int \frac{\sin t \cos a+\cos t \sin a}{\sin t} d t$

$=\int(\cos a+\cot t \sin a) d t$

$=t \cos a+\sin a \log |\sin t|+C_1$

$=(x-a) \cos a+\sin a \log |\sin (x-a)|+C_1$

$=x \cos a+\sin a \log |\sin (x-a)|-a \cos a+C_1$

$\left.=\sin a \log |\sin (x-a)|+x \cos a+C \quad \text { [Where } C=C_1-a \cos a\right]$

Question 8: $\int\frac{e^{5 \log x}-e^{4 \log x}}{e^{3 \log x}-e^{2 \log x}}dx$

Solution: Let $I=\int\frac{e^{5 \log x}-e^{4 \log x}}{e^{3 \log x}-e^{2 \log x}}dx$

$=\int\frac{e^{4 \log x}\left(e^{\log x}-1\right)}{e^{2 \log x}\left(e^{\log x}-1\right)}dx$

$=\int\frac{e^{4 \log x}}{e^{2 \log x}}dx$

$=\int \frac{x^4}{x^2}dx$

$=\int x^2dx$

$=\frac{x^3}{3}+C$

Question 9: $\int \frac{\cos x}{\sqrt{4-\sin ^2 x}}dx$

Solution: Let $I =\frac{\cos x}{\sqrt{4-\sin ^2 x}}$

Let $\sin x=t \Rightarrow \quad \cos x d x=d t$

$I=\int \frac{\cos x}{\sqrt{4-\sin ^2 x}} d x$

$=\sin ^{-1}\left(\frac{t}{2}\right)+C$

$=\sin ^{-1}\left(\frac{\sin x}{2}\right)+C$

Question 10: $\int\frac{\sin ^8 x-\cos ^8 x}{1-2 \sin ^2 x \cos ^2 x}dx$

Solution: Let $I=\int\frac{\sin ^8 x-\cos ^8 x}{1-2 \sin ^2 x \cos ^2 x}dx$

$=\int\frac{\left(\sin ^4 x+\cos ^4 x\right)\left(\sin ^4 x-\cos ^4 x\right)}{\sin ^2 x+\cos ^2 x-\sin ^2 x \cos ^2 x-\sin ^2 x \cos ^2 x}dx$

$=\int\frac{\left(\sin ^4 x+\cos ^4 x\right)\left(\sin ^2 x-\cos ^2 x\right)\left(\sin ^2 x+\cos ^2 x\right)}{\left(\sin ^2 x-\sin ^2 x \cos ^2 x\right)+\left(\cos ^2 x-\sin ^2 x \cos ^2 x\right)}dx$

$=\int\frac{\left(\sin ^4 x+\cos ^4 x\right)\left(\sin ^2 x-\cos ^2 x\right)}{\sin ^2 x\left(1-\cos ^2 x\right)+\cos ^2 x\left(1-\sin ^2 x\right)}dx$

$=\frac{\left(\sin ^4 x+\cos ^4 x\right)\left(\sin ^2 x-\cos ^2 x\right)}{\sin ^4 x+\cos ^4 x}dx$

$=-\int\cos 2 xdx$

$=-\frac{\sin 2 x}{2}+C$

Question 11: $\int\frac{1}{\cos (x+a) \cos (x+b)}dx$

Solution : Let $I= \int\frac{1}{\cos (x+a) \cos (x+b)}dx$

Multiplying and dividing by $\sin (a-b)$ , we have

$=\frac{1}{\sin (a-b)}\int\left[\frac{\sin (a-b)}{\cos (x+a) \cos (x+b)}\right]dx$

$=\frac{1}{\sin (a-b)}\int\left[\frac{\sin \{(x+a)-(x+b)\}}{\cos (x+a) \cos (x+b)}\right]dx$

$=\frac{1}{\sin (a-b)}\int\left[\frac{\sin (x+a) \cos (x+b)-\cos (x+a) \sin (x+b)}{\cos (x+a) \cos (x+b)}\right]dx$

$=\frac{1}{\sin (a-b)}\int\left[\frac{\sin (x+a)}{\cos (x+a)}-\frac{\sin (x+b)}{\cos (x+b)}\right]dx$

$=\frac{1}{\sin (a-b)}\int[\tan (x+a)-\tan (x+b)]dx$

$=\frac{1}{\sin (\mathrm{a}-\mathrm{b})}[-\log |\cos (x+a)|+\log |\cos (x+b)|]+C$

$=\frac{1}{\sin (\mathrm{a}-\mathrm{b})} \log \left|\frac{\cos (x+b)}{\cos (x+a)}\right|+C$

Question 12: $\int\frac{x^3}{\sqrt{1-x^8}}dx$

Solution: Let $I=\int \frac{x^3}{\sqrt{1-x^8}} d x$

$=\int \frac{x^3}{\sqrt{1-(x^4)^2}} d x$

Let $x^4 =t$

$\Rightarrow 4x^3dx=dt$

$\Rightarrow x^3dx=\frac{dt}{4}$

$I=\frac{1}{4}\int \frac{1}{\sqrt{1-t^2}} d x$

$=\frac{1}{4}\sin^{-1}t+C$

$=\frac{1}{4}\sin^{-1}x^4+C$

Question 13: $\int\frac{e^x}{(1+e^x)(2+e^x)}dx$

Solution: Let $I=\int\frac{e^x}{(1+e^x)(2+e^x)}dx$

Let $e^x =t\Rightarrow e^xdx=dt$

$I=\int\frac{1}{(1+t)(2+t)}dt$

Since,

$\frac{1}{(1+t)(2+t)}=\frac{A}{1+t}+\frac{B}{2+t}--(i)$

$\Rightarrow \frac{1}{(1+t)(2+t)}=\frac{A(2+t)+B(1+t)}{(1+t)(2+t)}$

$\Rightarrow 1=A(2+t)+B(1+t)$

Let $t=-1$

$1=A(2-1)+0$

$\Rightarrow A=1$

Again Let $t=-2$

$1=0+B(1-2)$

$\Rightarrow 1 = -B\Rightarrow B = -1$

Putting the value of A and B in (i) and integrate

$\int\frac{1}{(1+t)(2+t)}dt=\int\frac{1}{1+t}+\frac{-1}{2+t}dt$

$=\log |1+t|-\log |2+t|+C$

$=\log \left|\frac{1+t}{2+t}\right|+C$

$=\log \left|\frac{1+e^x}{2+e^x}\right|+C$

Question 14: $\int\frac{1}{(x^2+1)(x^2+4)}dx$

Solution: Let $I=\int\frac{1}{(x^2+1)(x^2+4)}dx$

Let $x^2=y$

$\frac{1}{(y+1)(y+4)}=\frac{A}{(y+1)}+\frac{B}{(y+4)}--(i)$

$\Rightarrow \frac{1}{(y+1)(y+4)}=\frac{A(y+4)+B(y+1)}{(y+1)(y+4)}$

$\Rightarrow 1=A(y+4)+B(y+1)$

Let $y=-1$

$1=A(-1+4)+0$

$\Rightarrow 1 = 3A\Rightarrow A=\frac{1}{3}$

Let $y= -4$

$1=0+B(-4+1)$

$\Rightarrow 1 =-3B\Rightarrow B = -\frac{1}{3}$

Putting the value of A and b and integrate

$\frac{1}{(y+1)(y+2)}=\frac{1/3}{(y+1)}+\frac{-1/3}{(y+4)}$

$\int\frac{1}{(x^2+1)(x^2+4)}dx=\int\frac{1/3}{(x^2+1)}+\frac{-1/3}{(x^2+4)}dx$

$=\frac{1}{3}\tan^{-1}x-\frac{1}{3\times 2}\tan^{-1}\frac{x}{2}+C$

$=\frac{1}{3}\tan^{-1}x-\frac{1}{6}\tan^{-1}\frac{x}{2}+C$

Question 15: $\int\cos ^3 x e^{\log \sin x}dx$

Solution : Let $I=\int \cos ^3 x e^{\log \sin x} d x$

$=\int \cos ^3 x \sin x d x \quad\left[\text { Since } e^{\log x}=x\right]$

Let $\cos x=t \quad \Rightarrow \sin x d x=d t$

$I=-\int t^3 d t$

$=-\int \frac{t^4}{4}+C$

$=-\frac{\cos ^4 x}{4}+C$

Question 16: $\int e^{3 \log x}\left(x^4+1\right)^{-1}dx$

Solution : Let $I=\int e^{3 \log x}\left(x^4+1\right)^{-1}dx$

$=\int e^{\log x^3}\left(x^4+1\right)^{-1}dx$

$=\int \frac{x^3}{\left(x^4+1\right)}dx \quad\left[\text { Since } e^{\log x}=x\right]$

Let $x^4+1=t \quad \Rightarrow 4 x^3 d x=d t$

$=\frac{1}{4}\int \frac{1}{t} d x$

$=\frac{1}{4} \log |t|+C$

$=\frac{1}{4} \log \left|x^4+1\right|+C$

$=\frac{1}{4} \log \left(x^4+1\right)+C$

Question 17: $\int f^{\prime}(a x+b)\left[\int(a x+b)\right]^ndx$

Solution : Let $I=\int f^{\prime}(a x+b)\left[\int(a x+b)\right]^n d x$

Let $\int(a x+b)=t \quad \Rightarrow a f^{\prime}(a x+b) d x=d t$

$I=\int f^{\prime}(a x+b)\left[\int(a x+b)\right]^n d x$

$=\frac{1}{a} \int t^n d t$

$=\frac{1}{a}\left[\frac{t^{n+1}}{n+1}\right]$

$=\frac{1}{a(n+1)}\left[\int(a x+b)\right]^{n+1}+C$

Question 18: $\int \frac{1}{\sqrt{\sin ^3 x \sin (x+a)}}dx$

Solution : Let $I= \frac{1}{\sqrt{\sin ^3 x \sin (x+a)}}dx$

$=\int\frac{1}{\sqrt{\sin ^3 x(\sin x \cos a+\cos x \sin a)}}dx$

$=\int \frac{1}{\sqrt{\left(\sin ^4 x \cos a+\sin ^3 x \cos x \sin a\right)}}dx$

$=\int \frac{1}{\sin ^2 x \sqrt{(\cos a+\cot x \sin a)}}dx$

$=\int \frac{\operatorname{cosec}^2 x}{\sqrt{(\cos a+\cot x \sin a)}}dx$

Let $\cos a+\cot x \sin a=t \quad \Rightarrow-\operatorname{cosec}^2 x \sin a d x=d t$

$I=\int \frac{1}{\sqrt{\sin ^3 x \sin (x+a)}} d x$

$=\int \frac{\operatorname{cosec}^2 x}{\sqrt{(\cos a+\cot x \sin a)}} d x$

$=\frac{-1}{\sin a} \int \frac{d t}{\sqrt{t}}$

$=\frac{-1}{\sin a}[2 \sqrt{t}]+C$

$=\frac{-2}{\sin a}\left[\sqrt{\cos a+\frac{\cos x \sin a}{\sin x}}\right]+C$

$=\frac{-2}{\sin a} \sqrt{\frac{\sin \mathrm{x} \cos \mathrm{a}+\cos x \sin a}{\sin x}}+C$

$=\frac{-2}{\sin a} \sqrt{\frac{\sin (x+a)}{\sin x}+C}$

Question 19: $\int \frac{\sin ^{-1} \sqrt{x}-\cos ^{-1} \sqrt{x}}{\sin ^{-1} \sqrt{x}+\cos ^{-1} \sqrt{x}}, x \in[0,1]$

Solution : Let $I=\int \frac{\sin ^{-1} \sqrt{x}-\cos ^{-1} \sqrt{x}}{\sin ^{-1} \sqrt{x}+\cos ^{-1} \sqrt{x}} d x$

We know that: $\sin ^{-1} \sqrt{x}+\cos ^{-1} \sqrt{x}=\frac{\pi}{2}$

Therefore, $\quad I=\int \frac{\left(\frac{\pi}{2}-\cos ^{-1} \sqrt{x}\right)-\cos ^{-1} \sqrt{x}}{\frac{\pi}{2}} d x$

$=\frac{2}{\pi} \int\left(\frac{\pi}{2}-2 \cos ^{-1} \sqrt{x}\right) d x$

$=\frac{2}{\pi} \cdot \frac{\pi}{2} \int 1 d x-\frac{2}{\pi} \cdot 2 \int \cos ^{-1} \sqrt{x} d x$

$I=x-\frac{4}{\pi} \int \cos ^{-1} \sqrt{x} d x$

Let $I_1=\int \cos ^{-1} \sqrt{x} d x \quad$ and let $\sqrt{x}=t \quad \Rightarrow d x=2 t d t$

$I_1=2 \int \cos ^{-1} t \cdot t d t$

$=2\left[\cos ^{-1} t \cdot \frac{t^2}{2}-\int \frac{-1}{\sqrt{1-t^2}} \cdot \frac{t^2}{2} d t\right]$

$=t^2 \cos ^{-1} t+\int \frac{t^2}{\sqrt{1-t^2}} d t$

$=t^2 \cos ^{-1} t-\int \frac{1-t^2-1}{\sqrt{1-t^2}} d t$

$=t^2 \cos ^{-1} t-\int \sqrt{1-t^2} d t+\int \frac{1}{\sqrt{1-t^2}} d t$

$=t^2 \cos ^{-1} t-\frac{t}{2} \sqrt{1-t^2} d t-\frac{1}{2} \sin ^{-1} t+\sin ^{-1} t$

$=t^2 \cos ^{-1} t-\frac{t}{2} \sqrt{1-t^2} d t+\frac{1}{2} \sin ^{-1} t$

From equation (1), we have

$I=x-\frac{4}{\pi}\left[t^2 \cos ^{-1} t-\frac{t}{2} \sqrt{1-t^2} d t+\frac{1}{2} \sin ^{-1} t\right]$

$\Rightarrow I=x-\frac{4}{\pi}\left[x \cos ^{-1} \sqrt{x}-\frac{\sqrt{x}}{2} \sqrt{1-x} d t+\frac{1}{2} \sin ^{-1} \sqrt{x}\right]$

$\Rightarrow I=x-\frac{4}{\pi}\left[x\left(\frac{\pi}{2}-\sin ^{-1} \sqrt{x}\right)-\frac{\sqrt{x-x^2}}{2}+\frac{1}{2} \sin ^{-1} \sqrt{x}\right]$

$\Rightarrow I=x-2 x+\frac{4}{\pi} \sin ^{-1} \sqrt{x}+\frac{2}{\pi} \sqrt{x-x^2}-\frac{2}{\pi} \sin ^{-1} \sqrt{x}$

$\Rightarrow I=-x+\frac{2}{\pi}\left[(2 x+1) \sin ^{-1} \sqrt{x}\right]+\frac{2}{\pi} \sqrt{x-x^2}+C$

$\Rightarrow I=\frac{2(2 x+1)}{\pi} \sin ^{-1} \sqrt{x}+\frac{2}{\pi} \sqrt{x-x^2}-x+C$

Question 20: $\int\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}dx$

Solution : Let $I=\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}} d x$

Let $x=cos ^2 \theta \quad \Rightarrow d x=-2 \sin \theta \cos \theta d \theta$

$I=\int \sqrt{\frac{1-\cos \theta}{1+\cos \theta}}(-2 \sin \theta \cos \theta) d \theta$

$=-\int \frac{2 \sin ^2 \frac{\theta}{2}}{2 \cos ^2 \frac{\theta}{2}}(\sin 2 \theta) d \theta$

$=-\int \sqrt{\tan \frac{\theta}{2}} \cdot 2 \sin \theta \cos \theta d \theta$

$=-2 \int \frac{\sin \frac{\theta}{2}}{\cos \frac{\theta}{2}}\left(2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}\right) \cos \theta d \theta$

$=-4 \int \sin ^2 \frac{\theta}{2} \cos \theta d \theta$

$=-4 \int \sin ^2 \frac{\theta}{2}\left(2 \cos ^2 \frac{\theta}{2}-1\right) d \theta$

$=-4 \int\left(2 \sin ^2 \frac{\theta}{2} \cos ^2 \frac{\theta}{2}-\sin ^2 \frac{\theta}{2}\right) d \theta$

$=-8 \int \sin ^2 \frac{\theta}{2} \cos ^2 \frac{\theta}{2} d \theta+4 \int \sin ^2 \frac{\theta}{2} d \theta$

$=-2 \int \sin ^2 \theta d \theta+4 \int \sin \frac{\theta}{2} d \theta$

$=-2 \int\left(\frac{1-\cos 2 \theta}{2}\right) d \theta+4 \int \frac{1-\cos \theta}{2} d \theta$

$=-2\left[\frac{\theta}{2}-\frac{\sin ^2 \theta}{4}\right]+4\left[\frac{\theta}{2}-\frac{\sin \theta}{2}\right]+C$

$=-\theta+\frac{\sin ^2 \theta}{2}+2 \theta-2 \sin \theta+C$

$=\theta+\frac{\sin 2 \theta}{2}-2 \sin \theta+C$

$=\theta+\frac{2 \sin \theta \cos \theta}{2}-2 \sin \theta+C$

$=\theta+\sqrt{1-\cos ^2 \theta} \cdot \cos \theta-2 \sqrt{1-\cos ^2 \theta}+C$

$=-2 \cos ^{-1} \sqrt{x}+\sqrt{1-x} \cdot \sqrt{x}-2 \sqrt{1-x}+C$

$=-2 \sqrt{1-x}+\cos ^{-1} \sqrt{x}+\sqrt{x(1-x)}+C$

$=-2 \sqrt{1-x}+\cos ^{-1} \sqrt{x}+\sqrt{\left(x-x^2\right)}+C$

Question 21: $\int\frac{2+\sin 2 x}{1+\cos 2 x} e^xdx$

Solution : Let $I=\int\left(\frac{2+\sin 2 x}{1+\cos 2 x}\right) e^x d x$

$=\int\left(\frac{2+2 \sin x \cos x}{2 \cos ^2 x}\right) e^x d x$

$=\int\left(\frac{1+\sin x \cos x}{\cos ^2 x}\right) e^x d x$

$=\int\left(\sec ^2 x+\tan x\right) e^x d x$

$\text { Let } f(x)=\tan x \Rightarrow f^{\prime}(x)=\sec ^2 x$

We know that: $I=\int\left\{f(x)+f^{\prime}(x)\right\} e^x d x$

Therefore, $\quad I=\int\left(\sec ^2 x+\tan x\right) e^x d x$

$=e^x f(x)+C$

$=e^x \tan x+C$

Question 22: $\int\frac{x^2+x+1}{(x+1)^2(x+2)}dx$

Solution: Let $\frac{x^2+x+1}{(x+1)^2(x+2)}=\frac{A}{(x+1)}+\frac{B}{(x+1)^2}+\frac{C}{(x+2)}$

$\Rightarrow \frac{x^2+x+1}{(x+1)^2(x+2)}=\frac{A(x+1)(x+2)+B(x+2)+C(x+1)^2}{(x+1)^2(x+2)}$

$\Rightarrow x^2+x+1=A(x+1)(x+2)+B(x+2)+C\left(x+1\right)^2$

Let $x=-1$

$(-1)^2-1+1=0+B(-1+2)+0$

$\Rightarrow 1 = B$

Let $x=-2$

$(-2)^2-2+1=0+0+C(-2+1)^2$

$\Rightarrow 3=C$

Let $x=0$

$0+0+1=A(0+1)(0+2)+B(0+2)+C(0+1)^2$

$\Rightarrow 1 =2A+2B+C$

$\Rightarrow 1= 2A +2\times 1+3$

$\Rightarrow 1=2A+5$

$\Rightarrow A = -2$

$A=-2, \quad B=1 \quad \text { and } \quad C=3$

From equation (1), we have

$\frac{x^2+x+1}{(x+1)^2(x+2)}=\frac{-2}{(x+1)}+\frac{1}{(x+1)^2}+\frac{3}{(x+2)}$

Therefore, $\quad I=\int \frac{x^2+x+1}{(x+1)^2(x+2)} d x$

$=-2 \int \frac{1}{(x+1)} d x+3 \int \frac{1}{(x+2)} d x+\int \frac{1}{(x+1)^2} d x$

$=-2 \log |x+1|+3 \log |x+2|-\frac{1}{(x+1)}+C$

Question 23: $\int\tan ^{-1} \sqrt{\frac{1-x}{1+x}} d x$

Solution :Let $I=\int \tan ^{-1} \sqrt{\frac{1-x}{1+x}} d x$

Let $x=\cos \theta \quad \Rightarrow d x=-\sin \theta d \theta$

$I =\int \tan ^{-1} \sqrt{\frac{1-\cos \theta}{1+\cos \theta}}(-\sin \theta d \theta)$

$=-\int \tan ^{-1} \sqrt{\frac{2 \sin ^2 \frac{\theta}{2}}{2 \cos ^2 \frac{\theta}{2}}} \sin \theta d \theta$

$=-\int \tan ^{-1} \tan \frac{\theta}{2} \cdot \sin \theta d \theta$

$=-\frac{1}{2} \int \theta \sin \theta d \theta$

$=-\frac{1}{2}\left[\theta(-\cos \theta)-\int 1 \cdot(-\cos \theta) d \theta\right]$

$=-\frac{1}{2}[-\theta \cos \theta+\sin \theta]$

$=\frac{1}{2} \theta \cos \theta-\frac{1}{2} \sqrt{1-\cos ^2 \theta}$

$=\frac{1}{2} \cos ^{-1} x \cdot x-\frac{1}{2} \sqrt{1-x^2}+C$

$=\frac{x}{2} \cos ^{-1} x-\frac{1}{2} \sqrt{1-x^2}+C$

$=\frac{1}{2}\left(x \cos ^{-1} x-\sqrt{1-x^2}\right)+C$

Question 24: $\int\frac{\sqrt{x^2+1}\left[\log \left(x^2+1\right)-2 \log x\right]}{x^4}dx$

Solution: Let $I=\int\frac{\sqrt{x^2+1}\left[\log \left(x^2+1\right)-2 \log x\right]}{x^4}dx$

$=\int\frac{\sqrt{x^2+1}}{x^4}\left[\log \left(x^2+1\right)-2 \log x\right]dx$

$=\int\frac{\sqrt{x^2+1}}{x^4}\left[\log \left(\frac{x^2+1}{x^2}\right)\right]dx$

$=\int\frac{\sqrt{x^2+1}}{x^4}\left[\log \left(1+\frac{1}{x^2}\right)\right]dx$

$=\int\frac{1}{x^3} \sqrt{\frac{x^2+1}{x^2}}\left[\log \left(1+\frac{1}{x^2}\right)\right]dx$

$=\int\frac{1}{x^3} \sqrt{1+\frac{1}{x^2}}\left[\log \left(1+\frac{1}{x^2}\right)\right]dx$

Let $1+\frac{1}{x^2}=t \quad \Rightarrow \frac{-2}{x^3} d x=d t$

Therefore, $\quad I=\int \frac{1}{x^3} \sqrt{1+\frac{1}{x^2}} \log \left(1+\frac{1}{x^2}\right) d x$

$=-\frac{1}{2} \int \sqrt{t} \log t d t$

$=-\frac{1}{2} \int t^{\frac{1}{2}} \cdot \log t d t$

Integrating by parts, we have

$I=-\frac{1}{2}\left[\log t \cdot \int t^{\frac{1}{2}} d t-\int\left\{\left(\frac{d}{d t} \log t\right) \int t^{\frac{1}{2}} d t\right\} d t\right]$

$=-\frac{1}{2}\left[\log t \cdot \frac{t^{\frac{3}{2}}}{\frac{3}{2}}-\int \frac{1}{t} \cdot \frac{t^{\frac{3}{2}}}{\frac{3}{2}} d t\right]$

$=-\frac{1}{2}\left[\frac{2}{3} t^{\frac{3}{2}} \log t-\frac{2}{3} \int t^{\frac{1}{2}} d t\right]$

$=-\frac{1}{2}\left[\frac{2}{3} t^{\frac{3}{2}} \log t-\frac{4}{9} \cdot t^{\frac{3}{2}}\right]$

$=\frac{1}{3} t^{\frac{3}{2}} \log t-\frac{2}{9} \cdot t^{\frac{3}{2}}$

$=\frac{1}{3}t^{3/2}\left[\log t-\frac{2}{3}\right]$

$=\frac{1}{3}\left(1+\frac{1}{x^2}\right)\left[\log(1+\frac{1}{x^2})-\frac{2}{3}\right]+C$

Evaluate the definite integrals in Exercises 25 to 33.

Question 25: $\int_{\pi/2}^\pi e^x\left(\frac{1-\sin x}{1-\cos x}\right)dx$

Solution: Let $I = \int_{\pi/2}^\pi e^x\left(\frac{1-\sin x}{1-\cos x}\right)dx$

$= \int_{\pi/2}^\pi e^x\left(\frac{1-2\sin{\frac{x}{2}}\cos{\frac{x}{2}}}{2\sin^2{\frac{x}{2}}}\right)dx$

$=\int_{\pi/2}^\pi e^x\left(\frac{1}{2\sin^2\frac{x}{2}}-\frac{2\sin\frac{x}{2}\cos\frac{x}{2}}{2\sin^2\frac{x}{2}}\right)dx$

$=\int_{\pi/2}^\pi e^x\left(\frac{\operatorname{cosec}^2\frac{x}{2}}{2}-\cot\frac{x}{2}\right)dx$

Let $f(x) = -\cot\frac{x}{2}$

$\Rightarrow f'(x)=\operatorname{cosec}^2\frac{x}{2}$

Therefore, $I = \int e^x(f(x)+f'(x))dx$

$I=e^xf(x)+C$

$I=-\left[e^x\cot\frac{x}{2}\right]_{\pi/2}^\pi$

$=-\left[e^{\pi}\cot\frac{\pi}{2}-e^{\frac{\pi}{2}}\cot\frac{\pi}{4} \right]$

$=-\left[e^{\pi}\times 0-e^{\frac{\pi}{2}}\times 1\right]$

$=e^{\frac{\pi}{2}}$

Question 26: $\int_0^{\pi/4}\frac{\sin x \cos x}{\cos^4x+\sin^4x}dx$

Solution: Let $I=\int_0^{\pi/4}\frac{\sin x \cos x}{\cos^4x+\sin^4x}dx$

Divide by $\cos^4x$ in numerator and denominator

$=\int_0^{\pi/4}\frac{\frac{\sin x\cos x}{\cos^4x}}{\frac{\cos^4x}{\cos^4x}+\frac{\sin^4x}{\cos^4x}}dx$

$=\int_0^{\pi/4}\frac{\tan x\sec^2x}{1+\tan^4x}dx$

Let $\tan^2x =t$

$\Rightarrow 2\tan x\sec^2xdx=dt$

$\Rightarrow \tan x\sec^2x = \frac{dt}{2}$

When $x=o,t=0$ and when $x=\frac{\pi}{2},t=1$

$I = \frac{1}{2}\int_0^1\frac{1}{1+t^2}dt$

$=\frac{1}{2}[\tan^{-1}t]_0^1$

$=\frac{1}{2}[\tan^{-1}1-\tan^{-1}0]=\frac{1}{2}[\frac{\pi}{4}]$

$=\frac{\pi}{8}$

Question 27: $\int_0^{\frac{\pi}{2}}\frac{\cos^2x}{\cos^2x+4\sin^2x}dx$

Solution: Let $I=\int_0^{\frac{\pi}{2}}\frac{\cos^2x}{\cos^2x+4\sin^2x}dx$

$=\int_0^{\frac{\pi}{2}}\frac{\cos^2x}{\cos^2x+4(1-\cos^2x)}dx$

$=-\frac{1}{3}\int_0^{\frac{\pi}{2}}\frac{-3\cos^2x}{4-3\cos^2x}dx$

$=-\frac{1}{3}\int_0^{\frac{\pi}{2}}\frac{4-3\cos^2x-4}{4-3\cos^2x}dx$

$=-\frac{1}{3}\left[\int_0^{\frac{\pi}{2}}\frac{4-3\cos^2x}{4-3\cos^2x}dx-\int_0^{\frac{\pi}{2}}\frac{4}{4-3\cos^2x}dx\right]$

$=-\frac{1}{3}\int_0^{\frac{\pi}{2}}1dx+\frac{4}{3}\int_0^{\frac{\pi}{2}}\frac{1}{4-3\cos^2x}dx$

$=-\frac{1}{3}[x]_0^{\pi/2}+\frac{4}{3}\int_0^{\frac{\pi}{2}}\frac{\sec^2x}{4\sec^2x-3}dx$

$=-\frac{1}{3}[\frac{\pi}{2}-0]+\frac{4}{3}\int_0^{\frac{\pi}{2}}\frac{\sec^2x}{4(1+\tan^2x)-3}dx$

$=-\frac{\pi}{6}+\frac{4}{3}\int_0^{\frac{\pi}{2}}\frac{\sec^2x}{1+4\tan^2x}dx$

$=-\frac{\pi}{6}+\frac{4}{3}\int_0^{\frac{\pi}{2}}\frac{\sec^2x}{1+(2\tan x)^2}dx$

Let $2\tan x =t\Rightarrow 2\sec^2x dx=dt$

$\Rightarrow \sec^2x dx=\frac{dt}{2}$

When $x=0,t=0$ and when $x=\frac{\pi}{2},t=\infty$

$I=-\frac{\pi}{6}+\frac{4}{3}\int_0^{\infty}\frac{1}{1+t^2}\frac{dt}{2}$

$=-\frac{\pi}{6}+\frac{2}{3}\int_0^{\infty}\frac{1}{1+t^2}dt$

$=-\frac{\pi}{6}+\frac{2}{3}\left[\tan^{-1}t\right]_0^\infty$

$=-\frac{\pi}{6}+\frac{2}{3}\left[\tan^{-1}\infty-\tan^{-1}0 \right]$

$=-\frac{\pi}{6}+\frac{2}{3}\left[\frac{\pi}{2}-0 \right]$

$=-\frac{\pi}{6}+\frac{\pi}{3}$

$=\frac{\pi}{6}$

Question 28: $\int_{\pi/6}^{\pi/3}\frac{\sin x+\cos x}{\sqrt{\sin 2x}}dx$

Solution: Let $I=\int_{\pi/6}^{\pi/3}\frac{\sin x+\cos x}{\sqrt{\sin 2x}}dx$

Let $\sin x-\cos x=t$

$\Rightarrow (\cos x+\sin x)dx=dt$

Again taking $\sin x-\cos x=t$

Squaring both side

$(\sin x-\cos x)^2=t^2$

$\Rightarrow \sin^2x+\cos^2x-2\sin x\cos x=t^2$

$\Rightarrow 1-\sin 2x=t^2$

$\Rightarrow \sin 2x = 1-t^2$

When $x =\frac{\pi}{6},t= \sin\frac{\pi}{6}-\cos\frac{\pi}{6}$
$=\frac{1}{2}-\frac{\sqrt{3}}{2}=-(\frac{\sqrt{3}-1}{2})$

and When $x =\frac{\pi}{3},t= \sin\frac{\pi}{3}-\cos\frac{\pi}{3}$
$=\frac{\sqrt{3}}{2}-\frac{1}{2}=(\frac{\sqrt{3}-1}{2})$

Now

$I=\displaystyle\int_{-(\frac{\sqrt{3}-1}{2})}^{(\frac{\sqrt{3}-1}{2})}\frac{1}{\sqrt{1-t^2}}dt$

$=\left[\sin^{-1}t\right]_{-(\frac{\sqrt{3}-1}{2})}^{(\frac{\sqrt{3}-1}{2})}$

$=\sin^{-1}{(\frac{\sqrt{3}-1}{2})}-\sin^{-1}\{-(\frac{\sqrt{3}-1}{2})\}$

$=\sin^{-1}{(\frac{\sqrt{3}-1}{2})}+\sin^{-1}(\frac{\sqrt{3}-1}{2})$

$=2\sin^{-1}{(\frac{\sqrt{3}-1}{2})}$

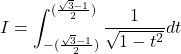
Question 29: $\int_0^1\frac{1}{\sqrt{1+x}-\sqrt{x}}dx$

Solution: Let $I=\int_0^1\frac{1}{\sqrt{1+x}-\sqrt{x}}dx$

$=\int_0^1\frac{1}{\sqrt{1+x}-\sqrt{x}}\times\frac{\sqrt{1+x}+\sqrt{x}}{\sqrt{1+x}+\sqrt{x}}dx$

$=\int_0^1 \frac{\sqrt{1+x}+\sqrt{x}}{1+x-x}dx$

$=\int_0^1\sqrt{1+x}+\sqrt{x}dx$

$=\left[\frac{(1+x)^{3/2}}{3/2}-\frac{x^{3/2}}{3/2}\right]_0^1$

$=\frac{2}{3}\left[(1+x)^{3/2}-x^{3/2}\right]_0^1$

$=\frac{2}{3}\left[\left((1+1)^{3/2}+(1)^{3/2}\right)-\left((1+0)^{3/2}+0\right)\right]$

$\frac{2}{3}[2\sqrt{2}+1-1]$

$=\frac{4\sqrt{2}}{3}$

Question 30: $\int_0^{\frac{\pi}{4}}\frac{\sin x+\cos x}{9+16\sin 2x}dx$

Solution: Let $I=\int_0^{\frac{\pi}{4}}\frac{\sin x+\cos x}{9+16\sin 2x}dx$

Let $\sin x-\cos x=t$

$\Rightarrow (\cos x+\sin x)dx=dt$

Again taking $\sin x-\cos x=t$

Squaring both side

$(\sin x-\cos x)^2=t^2$

$\Rightarrow \sin^2x+\cos^2x-2\sin x\cos x=t^2$

$\Rightarrow 1-\sin 2x=t^2$

$\Rightarrow \sin 2x = 1-t^2$

When $x =0,t= \sin0-\cos0=-1$

and When $x =\frac{\pi}{4},t= \sin\frac{\pi}{4}-\cos\frac{\pi}{4}$
$=\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=0$

Now

$I=\int_{-1}^0\frac{1}{9+16(1-t^2)}dt$

$=\int_{-1}^0\frac{1}{25-16t^2}dt$

$=\int_{-1}^0\frac{1}{(5)^2-(4t)^2}dt$

$=\frac{1}{4}\left[\frac{1}{2(5)}\log\left|\frac{5+4t}{5-4t}\right|\right]_{-1}^0$

$=\frac{1}{40}\left[\log|1|-\log\left|\frac{1}{9}\right|\right]$

$=\frac{1}{40}\log 9$

Question 31: $\int_0^{\frac{\pi}{2}}\sin2x\tan^{-1}(\sin x)dx$

Solution: Let $I=\int_0^{\frac{\pi}{2}}\sin2x\tan^{-1}(\sin x)dx$

$=\int_0^{\frac{\pi}{2}}2\sin x\cos x\tan^{-1}(\sin x)dx$

Let $\sin x=t\Rightarrow \cos x dx=dt$

When $x=0,t=0$ and when $x=\frac{\pi}{2}, t=1$

$I=\int_0^12t\tan^{-1}tdt$

$=2\int_0^1\tan^{-1}tdt$

$=2\left[\tan^{-1}t\int t-\int\{\frac{d}{dt}\tan^{-1}t\int t dt\}dt\right]_0^1$

$=2\left[\tan^{-1}t\times \frac{t^2}{2}-\int\frac{1}{1+t^2}\times\frac{t^2}{2}dt\right]$

$=2\left[\frac{t^2}{2}\tan^{-1}t-\frac{1}{2}\int \frac{t^2+1-1}{1+t^2}dt\right]_0^1$

$=2\left[\frac{t^2}{2}\tan^{-1}t-\frac{1}{2}\int1-\frac{1}{1+t^2}dt\right]_0^1$

$=2\left[\frac{t^2}{2}\tan^{-1}t-\frac{1}{2}(t-\tan^{-1}t)\right]_0^1$

$=\left[t^2\tan^{-1}t-t+\tan^{-1}t\right]_0^1$

$=\left[(1\times \tan^{-1}1-1+\tan^{-1}1)-(0-0+0)\right]$

$=\left[\frac{\pi}{4}-1+\frac{\pi}{4}\right]$

$=\frac{\pi}{2}-1$

Question 32: $\int_0^\pi\frac{x\sec x}{\sec x+\tan x}dx$

Solution: Let $I=\int_0^\pi\frac{x\sec x}{\sec x+\tan x}dx--(i)$

$\left[using property: \int_0^a f(x) dx=\int_0^af(a-x)dx\right]$

$I=\int_0^\pi\frac{(\pi-x)\sec(\pi- x)}{\sec (\pi-x)+\tan (\pi-x)}dx$

$I=\int_0^\pi\frac{-(\pi-x)\sec x}{-\sec x-\tan x}dx$

$I=\int_0^\pi\frac{(\pi-x)\sec x}{\sec x+\tan x}dx--(ii)$

Adding (i) and (ii)

$2I=\int_0^\pi\frac{x\sec x}{\sec x+\tan x}+\frac{(\pi-x)\sec x}{\sec x+\tan x}dx$

$\Rightarrow 2I=\int_0^\pi\frac{\pi\sec x}{\sec x+\tan x}dx$

$\Rightarrow 2I = \pi\int_0^\pi\frac{\tan x}{\sec x+\tan x}\times \frac{\sec x-\tan x}{\sec x-\tan x}dx$

$\Rightarrow 2I=\pi\int_0^\pi\frac{\tan x(\sec x-\tan x)}{\sec^2x-\tan^2x}dx$

$\Rightarrow 2I=\pi\int_0^\pi \sec x\tan x-\tan^2xdx$

$\Rightarrow 2I=\pi\int_0^\pi \sec x\tan x-(\sec^2x-1)dx$

$\Rightarrow 2I=\pi\int_0^\pi \sec x\tan x-\sec^2x+1dx$

$\Rightarrow 2I =\pi\left[\sec x-\tan x+x\right]_0^\pi$

$\Rightarrow I = \frac{\pi}{2}\left[(\sec\pi-\tan\pi+\pi)-(\sec 0-\tan 0+0)\right]$

$\Rightarrow I= \frac{\pi}{2}\left[(-1-0+\pi)-(1-0+0)\right]$

$=\frac{\pi}{2}[\pi-2]$

Question 33: $\int_1^4 |x-1|+|x-2|+|x-3|dx$

Solution: Let $I=\int_1^4 |x-1|+|x-2|+|x-3|dx$

$I=\int_1^4|x-1|dx+\int_1^4|x-2|dx+\int_1.^4|x-3|dx$

$=\int_1^4(x-1)dx+\int_1^2-(x-2)dx+\int_2^4(x-2)dx+\int_1^3-(x-3)dx+\int_3^4(x-3)dx$

$=(\frac{x^2}{2}-x)_1^4-(\frac{x^2}{2}-2x)_1^2 +(\frac{x^2}{2}-2x)_2^4-(\frac{x^2}{2}-3x)_1^3+(\frac{x^2}{2}-3x)_3^4$

$=[(8-4)-(\frac{1}{2}-1)]-[(2-4)-(\frac{1}{2}-2)]+[(8-8)-(2-4)]-[(\frac{9}{2}-9)-(\frac{1}{2}-3)]+[(8-12)-(\frac{9}{2}-9)]$

$=[4+\frac{1}{2}]-[-2+\frac{3}{2}]+[0+2]-[-\frac{9}{2}+\frac{5}{2}]+[-4+\frac{9}{2}]$

$=\frac{9}{2}+\frac{1}{2}+2+2+\frac{1}{2}$

$=\frac{11}{2}+4$

$=\frac{19}{2}$

Prove the following (Exercises 34 to 39)

Question 34: $\int_{\text{1}}^{\text{3}}{\dfrac{\text{dx}}{{{\text{x}}^{\text{2}}}\left( \text{x+1} \right)}}\text{=}\dfrac{\text{2}}{\text{3}}\text{+log}\dfrac{\text{2}}{\text{3}}.$

Solution: Let $I=\int_{1}^{3}{\dfrac{dx}{{{x}^{2}}\left( x+1 \right)}}$

$\therefore \dfrac{1}{{{x}^{2}}\left( x+1 \right)}=\dfrac{A}{x}+\dfrac{B}{{{x}^{2}}}+\dfrac{C}{\left( x+1 \right)}--(i)$

$\Rightarrow 1=Ax\left( x+1 \right)+B\left( x+1 \right)+C\left( {{x}^{2}} \right)$

Let $x=0$

$1=0+B(0+1)+0\Rightarrow B=1$

Let $x=-1$

$1= 0+0+C(-1)^2$

$\Rightarrow 1 = C$

Let $x=1$

$1=A(1)(1+1)+B(1+1)+C(1)^2$

$\Rightarrow 1 = 2A+2B+C$

$\Rightarrow 1 = 2A+2(1)+1$

$\Rightarrow A=-1$

$A=-1,\,B=1,\,C=1$ respectively.

Putting the value in eq (i) and integrate

$I=\int_{1}^{3}{\dfrac{dx}{{{x}^{2}}\left( x+1 \right)}}=\int_{1}^{3}{\left\{ \dfrac{-1}{x}+\dfrac{1}{{{x}^{2}}}+\dfrac{1}{\left( x+1 \right)} \right\}dx}$

$\Rightarrow I=\left[ -\log x-\dfrac{1}{x}+\log \left( x+1 \right) \right]_{1}^{3}$

$=\left[ \log \left( \dfrac{x+1}{x} \right)-\dfrac{1}{x} \right]_{1}^{3}$

$=\left[\log \left( \dfrac{4}{3} \right)-\dfrac{1}{3}\right]-\left[\log \left( 2 \right)-1\right]$

$\Rightarrow I=\log 4-\log 3-\log 2+\dfrac{2}{3}$

$=\log 2-\log 3+\dfrac{2}{3}$

$=\log \left( \dfrac{2}{3} \right)+\dfrac{2}{3}$

Hence proved.

Question 35: $\int_{\text{0}}^{\text{1}}{\text{x}{{\text{e}}^{\text{x}}}\text{dx}}\text{=1}.$

Solution: Let $I=\int_{0}^{1}{x{{e}^{x}}dx}$

$\Rightarrow I=x\int_{0}^{1}{{{e}^{x}}dx}-\int_{0}^{1}{\left\{ \left( \dfrac{d\left( x \right)}{dx} \right)\int{{{e}^{x}}}dx \right\}}dx$

$=\left[ x{{e}^{x}} \right]_{0}^{1}-\left[ {{e}^{x}} \right]_{0}^{1}$

$=e-e+1=1$

Hence proved.

Question 36: $\int_{-1}^{1}{{{\text{x}}^{\text{17}}}\text{co}{{\text{s}}^{\text{4}}}\text{xdx}}\text{=0}.$

Solution: Let $I= \int_{-1}^{1}{{{x}^{17}}{{\cos }^{4}}xdx}$

Now, consider $f(x)={{x}^{17}}{{\cos }^{4}}x$

$\therefore f\left( -x \right)={{\left( -x \right)}^{17}}{{\cos }^{4}}\left( -x \right)$

$=-{{x}^{17}}{{\cos }^{4}}x=-f\left( x \right)$

$\Rightarrow f( x)$ is an odd function and hence it is clearly known to us that when f(x) is an odd function, then $\int_{-a}^{a}{f\left( x \right)dx}=0.$

$\therefore I=\int_{1}^{-1}{{{x}^{17}}{{\cos }^{4}}xdx}=0$

Hence proved.

Question 37: $\int_{\text{0}}^{\frac{\pi}{2}}\sin^3xdx\text{=}\dfrac{\text{2}}{\text{3}}.$

Solution: Let $I=\int_{0}^{\dfrac{\pi }{2}}{{{\sin }^{3}}xdx}$

$\Rightarrow I=\int_{0}^{\frac{\pi }{2}}{{{\sin }^{2}}x\sin xdx}$

$=\int_{0}^{\frac{\pi }{2}}{\left( 1-{{\cos }^{2}}x \right)\sin xdx}$

$=\int_{0}^{\frac{\pi }{2}}{\sin xdx}-\int_{0}^{\frac{\pi }{2}}{{{\cos }^{2}}x\sin xdx}$

Let $\cos x=t$

$\Rightarrow -\sin xdx=dt$

$\Rightarrow \sin xdx=-dt$

$I=-[\cos x]_0^{\frac{\pi}{2}}+\int_0^{\frac{\pi}{2}}t^2dt$

$=-[\cos \frac{\pi}{2}-\cos 0]+[\frac{t^3}{3}]_0^{\frac{\pi}{2}}$

$=-[0-1]+\frac{1}{3}[\cos^3x]_0^{\frac{\pi}{2}}$

$=1+\frac{1}{3}[\cos^3\frac{\pi}{2}-\cos^30]$

$=1+\frac{1}{3}[0-1]=1-\frac{1}{3}$

$=\frac{2}{3}$

Hence proved.

Queston 38: $\int_{\text{0}}^{\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}}{\text{2ta}{{\text{n}}^{\text{3}}}\text{xdx}}\text{=1-log2}.$

Solution: Let $I=\int_{0}^{\frac{\pi }{4}}{2{{\tan }^{3}}xdx}$

$\Rightarrow I=\int_{0}^{\dfrac{\pi }{4}}{2{{\tan }^{2}}x\tan xdx}$

$=2\int_{0}^{\dfrac{\pi }{4}}{\left( {{\sec }^{2}}x -1\right)\tan xdx}$

$=2\int_{0}^{\dfrac{\pi }{4}}{{{\sec }^{2}}x\tan xdx}-2\int_{0}^{\dfrac{\pi }{4}}{\tan xdx}$

Let $\tan x=t$

$\Rightarrow \sec^2xdx=dt$

When $x =0, t=0$ and when $x=\frac{\pi}{4},t=1$

$I=2\int_0^1tdt-2\left[ \log \sec x \right]_{0}^{\dfrac{\pi }{4}}$

$=2[\frac{t^2}{2}]_0^1-2\left[ \log \sec \dfrac{\pi }{4}-\log \cos 0 \right]$

$=[1-0]-2[\log \sqrt{2}-0]$

$=1-2(\frac{1}{2})\log 2$

$=1-\log 2$

Hence proved

Question 39: $\int_{\text{0}}^{\text{1}}{\text{si}{{\text{n}}^{-1}}\text{xdx}}\text{=}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{-1}.$

Solution: Let $I= \int_{0}^{1}{{{\sin }^{-1}}xdx}$

$\Rightarrow I=\int_{0}^{1}{{{\sin }^{-1}}x.1dx}$

$\Rightarrow I=\sin^{-1}x\int_0^1 1dx-\int_0^1\left[\frac{d}{dx}\sin^{-1}x\int 1dx\right]dx$

$=\left[ {{\sin }^{-1}}x.x \right]_{0}^{1}-\int_{0}^{1}{\dfrac{1}{\sqrt{1-{{x}^{2}}}}xdx}$

$=\left[ x{{\sin }^{-1}}x \right]_{0}^{1}+\dfrac{1}{2}\int_{0}^{1}{\dfrac{\left( -2x \right)}{\sqrt{1-{{x}^{2}}}}dx}$

Let $1-{{x}^{2}}=t$

$\therefore \left( -2x \right)dx=dt$

when $x=0,\,t=1$ and when $x=1,\,t=0.$

$\therefore I=\left[ x{{\sin }^{-1}}x \right]_{0}^{1}+\dfrac{1}{2}\int_{0}^{1}{\dfrac{dt}{\sqrt{t}}}$

$=\left[ x{{\sin }^{-1}}x \right]_{0}^{1}+\dfrac{1}{2}\left[ 2\sqrt{t} \right]_{1}^{0}$

$={{\sin }^{-1}}1-\sqrt{1}$

$=\dfrac{\pi }{2}-1$

Hence proved.

Question 40: Evaluate $\int_{\text{0}}^{\text{1}}{{{\text{e}}^{\text{2-3x}}}}dx$ as a limit of sum.

Solution: Let $I=\int_{0}^{1}{{{e}^{2-3x}}}dx$

$\int_{a}^{b}{f(x)dx}=\left( b-a \right)\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ f\left( a \right)+f(a+h)+...+f(a+(n-1)h) \right],$

where, $h=\dfrac{b-a}{n}$

In this case, $a=0,\,b=1,\,f\left( x \right)={{e}^{2-3x}}$

$\Rightarrow h=\dfrac{1-0}{n}=\dfrac{1}{n}$

$\therefore \int_{0}^{1}{{{e}^{2-3x}}dx}=\left( 1-0 \right)\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ f\left( 0 \right)+f(0+h)+...+f(0+(n-1)h) \right]$

$\Rightarrow \int_{0}^{1}{{{e}^{2-3x}}dx}=\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{e}^{2}}+{{e}^{2-3h}}+...+{{e}^{2-3\left( n-1 \right)h}} \right]$

$=\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{e}^{2}}\left( 1+{{e}^{-3h}}+{{e}^{-6h}}...+{{e}^{-3\left( n-1 \right)h}} \right) \right]$

$\Rightarrow \int_{0}^{1}{{{e}^{2-3x}}dx}=\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{1}{n}\left[ {{e}^{2}}\left( \dfrac{1-{{e}^{\dfrac{-3}{n}.n}}}{1-{{e}^{\dfrac{-3}{n}}}} \right) \right]$

$\Rightarrow \int_{0}^{1}{{{e}^{2-3x}}dx}={{e}^{2}}\left( {{e}^{-3}}-1 \right)\underset{n\to \infty }{\mathop{\lim }}\,\dfrac{-1}{3}\left[ \dfrac{\dfrac{-3}{n}}{{{e}^{\dfrac{-3}{n}}}-1} \right]$

$=\dfrac{-{{e}^{2}}\left( {{e}^{-3}}-1 \right)}{3}$

$=\dfrac{-{{e}^{-1}}+{{e}^{2}}}{3}$

$=\dfrac{1}{3}\left( {{e}^{2}}-\dfrac{1}{e} \right)$

Choose the correct answers in Exercises 41 to 44.

Question 41: $\int{\dfrac{\text{dx}}{{{\text{e}}^{\text{x}}}\text{+}{{\text{e}}^{\text{-x}}}}}$ is equal to

A. $\text{ta}{{\text{n}}^{\text{-1}}}\left( {{\text{e}}^{\text{x}}} \right)\text{+C}$

B. $\text{ta}{{\text{n}}^{\text{-1}}}\left( {{\text{e}}^{\text{-x}}} \right)\text{+C}$

C. $\text{log}\left( {{\text{e}}^{\text{x}}}\text{-}{{\text{e}}^{\text{-x}}} \right)\text{+C}$

D. $\text{log}\left( {{\text{e}}^{\text{x}}}\text{+}{{\text{e}}^{\text{-x}}} \right)\text{+C}$

Solution: The correct answer is option (A)

Let $I=\int{\dfrac{dx}{{{e}^{x}}+{{e}^{-x}}}}$ .

Let ${{e}^{x}}=t$

$\therefore {{e}^{x}}dx=dt$

$\therefore I=\int{\dfrac{dx}{{{e}^{x}}+{{e}^{-x}}}}$

$=\int{\dfrac{1}{1+{{t}^{2}}}dt}$

$=\int{{{\tan }^{-1}}\operatorname{t}dt}+C$ , where C is any arbitrary constant.

Hence, the correct answer is option (A).

Question 42: $\int{\dfrac{\cos2x}{{{\left( \text{sinx+cosx} \right)}^{\text{2}}}}\text{dx}}$ is equal to

A. $\dfrac{\text{-1}}{\text{sinx+cosx}}\text{+C}$

B. $\text{log}\left| \text{sinx+cosx} \right|\text{+C}$

C. $\text{log}\left| \text{sinx-cosx} \right|\text{+C}$

D. $\dfrac{\text{1}}{{{\left( \text{sinx+cosx} \right)}^{\text{2}}}}\text{+C}$

Solution : The correct answer is option (B)

Let $I=\int{\dfrac{\cos 2x}{{{\left( \sin x+\cos x \right)}^{2}}}dx}.$

$=\int{\dfrac{\cos ^2x-\sin^2x}{{{\left( \sin x+\cos x \right)}^{2}}}dx}.$

$\Rightarrow I=\int{\dfrac{(\sin x+\cos x)(\cos x-\sin x)}{{{\left( \sin x+\cos x \right)}^{2}}}dx}$

$=\int{\dfrac{(\cos x-\sin x)}{\left( \sin x+\cos x \right)}dx}$

Let $\left( \sin x+\cos x \right)=t$

$\therefore (\cos x-\sin x)dx=dt$

$\therefore I=\int{\dfrac{1}{t}}dt$

$=\log \left| t \right|+C$

$={\log \left| \cos x+\sin x \right|+C},$ where C is any arbitrary constant.

Hence, the correct answer is option (B).

Question 43: If $\text{f}\left( \text{a+b-x} \right)\text{=f}\left( \text{x} \right)\text{,}\,then \int_{\text{a}}^{\text{b}}{\text{xf}\left( \text{x} \right)\text{dx}}$ is equal to

A. $\dfrac{\text{a+b}}{\text{2}}\int_{\text{a}}^{\text{b}}{\text{f}\left( \text{b-x} \right)\text{dx}}$

B. $\dfrac{\text{a+b}}{\text{2}}\int_{\text{a}}^{\text{b}}{\text{f}\left( \text{b+x} \right)\text{dx}}$

C. $\dfrac{\text{b-a}}{\text{2}}\int_{\text{a}}^{\text{b}}{\text{f}\left( \text{x} \right)\text{dx}}$

D. $\dfrac{\text{a+b}}{\text{2}}\int_{\text{a}}^{\text{b}}{\text{f}\left( \text{x} \right)\text{dx}}$

Solution: The correct answer is option (D)

Let $I=\int_{a}^{b}{xf\left( x \right)dx}--(i)$

$\left[ \because \int_{a}^{b}{f\left( x \right)dx}=\int_{a}^{b}{f\left( a+b-x \right)dx} \right]$

$I=\int_{a}^{b}{\left( a+b-x \right)f\left( a+b-x \right)dx}--(ii)$

From (i) and (ii)

$\Rightarrow I=\int_{a}^{b}{\left( a+b-x \right)f\left( x \right)dx}=\left( a+b \right)\int_{a}^{b}{f\left( x \right)dx}-I using \left( 1 \right)$

$\Rightarrow 2I=\left( a+b \right)\int_{a}^{b}{f\left( x \right)dx}$

$\Rightarrow I=\dfrac{\left( a+b \right)}{2}\int_{a}^{b}{f\left( x \right)dx}$

Hence, the correct answer is option (D).

Question 44: The value of $\int_{\text{0}}^{\text{1}}{\text{ta}{{\text{n}}^{\text{-1}}}\left( \dfrac{\text{2x-1}}{\text{1+x-}{{\text{x}}^{\text{2}}}} \right)\text{dx}}$ is equal to