Class 12 ncert solution math exercise 1.2

With step-by-step explanations and a focus on clarity, these Class 12 NCERT solutions for Math Exercise 1.2 empower students to grasp the nuances of functions, setting a strong foundation for further mathematical exploration. Whether you’re gearing up for exams or aiming for a deeper understanding, these solutions make the journey through Class 12 Mathematics a rewarding and enlightening experience.

Exercise 1.2

Question 1: Show that the function $f: R_{*} \rightarrow R_{*}$ defined by $(x)=\frac{1}{x}$ is one-one and onto, where $R_{\text {o is }}$ the set of all non-zero real numbers. Is the result true, if the domain $R_{\cdot}$ is replaced by $\mathrm{N}$ with codomain being same as $R \cdot ?$ (Class 12 ncert solution math exercise 1.2 )

Solution: $f: R_{\bullet} \rightarrow R_{\bullet} \text { is by } f(x)=\frac{1}{x}$

For one-one:

$x, y \in R _* \text { such that } f(x)=f(y)$
$\Rightarrow \frac{1}{x}=\frac{1}{y}$
$\Rightarrow x=y$

$\therefore f$ is one-one.

For onto:

For $y \in R$ , there exists $x=\frac{1}{y} \in R \cdot[$ as $y \neq 0]$ such that

$f(x)=\frac{1}{\left(\frac{1}{y}\right)}=y$

$\therefore f$ is onto.

Given function $f$ is one-one and onto. Consider function $g: N \rightarrow R$ • defined by $g(x)=\frac{1}{x}$

We have, $g\left(x_{1}\right)=g\left(x_{2}\right) \Rightarrow \frac{1}{x_{1}}=\frac{1}{x_{2}} \Rightarrow x_{1}=x_{2}$

$\therefore g$ is one-one.

$g$ is not onto as for $1.2 \in R$ . there exist any $x$ in $N$ such that $g(x)=\frac{1}{1.2}$

Function $g$ is one-one but not onto.

Question 2:Check the injectivity and surjectivity of the following functions:

i. $f: N \rightarrow N$ given by $f(x)=x^{2}$

ii. $f: Z \rightarrow Z$ given by $f(x)=x^{2}$

iii. $f: R \rightarrow R$ given by $f(x)=x^{2}$

iv $f: N \rightarrow N$ given by $f(x)=x^{3}$

v. $f: Z \rightarrow Z$ given by $f(x)=x^{3}$

Solution:i. For $f: N \rightarrow N$ given by $f(x)=x^{2}$

$x, y \in N$

$f(x)=f(y) \Rightarrow x^{2}=y^{2} \Rightarrow x=y$

$\therefore f$ is injective. $2 \in N$ . But, there does not exist any $x$ in $N$ such that $f(x)=x^{2}=2\Rightarrow x=\sqrt2\notin N$

$\therefore f$ is not surjective

Function $f$ is injective but not surjective.

ii. $f: Z \rightarrow Z$ given by $f(x)=x^{2}$

$f(-1)=f(1)=1$ but $-1 \neq 1$

$\therefore f$ is not injective.

$-2 \in Z$ But, there does not exist any $x \in Z$ such that $f(x)=-2 \Rightarrow x^{2}=-2$

$\therefore f$ is not surjective.

Function $f$ is neither injective nor surjective.

iii. $f: R \rightarrow R$ given by $f(x)=x^{2}$

$f(-1)=f(1)=1$ but $-1 \neq 1$

$\therefore f$ is not injective.

$-2 \in Z$ But, there does not exist any $x \in Z$ such that $f(x)=-2 \Rightarrow x^{2}=-2$

$\therefore f$ is not surjective.

Function $f$ is neither injective nor surjective.

iv. $f: N \rightarrow N$ given by $f(x)=x^{3}$

$x, y \in N$

$f(x)=f(y) \Rightarrow x^{3}=y^{3} \Rightarrow x=y$

$\therefore f$ is injective.

$2 \in N$ . But, there does not exist any $x$ in $N$ such that $f(x)=x^{3}=2$

$\therefore f$ is not surjective

Function $f$ is injective but not surjective.

v. $f: Z \rightarrow Z$ given by $f(x)=x^{3}$

$x, y \in Z$

$f(x)=f(y) \Rightarrow x^{3}=y^{3} \Rightarrow x=y$

$\therefore f$ is injective.

$2 \in Z$ . But, there does not exist any $x$ in $Z$ such that $f(x)=x^{3}=2$

$\therefore f$ is not surjective.

Function $f$ is injective but not surjective.

Question 3:Prove that the greatest integer function $f: R \rightarrow R$ given by $f(x)=[x]_{\text {is neither one-one nor }}$ onto, where $[x]$ denotes the greatest integer less than or equal to $x$ .

Solution: $f: R \rightarrow R$ given by $f(x)=[x]$

$f(1.2)=[1.2]=1, f(1.9)=[1.9]=1$

$\therefore f(1.2)=f(1.9)$ , but $1.2 \neq 1.9$

$\therefore f$ is not one-one.

Consider $0.7 \in R$

$f(x)=[x]_{\text {is an integer. There does not exist any element }} x \in R$ such that $f(x)=0.7$

$\therefore f$ is not onto.

The greatest integer function is neither one-one nor onto.

Question 4:Show that the modulus function $f: R \rightarrow R$ given by $f(x)=|x|$ is neither one-one nor onto, where $|x|$ is $x$ , if $x$ is positive or 0 and $|x|$ is $-x$ , if $x$ is negative.

Solution: $f: R \rightarrow R$ is $f(x)=|x|=\left\{\begin{array}{l}\mathrm{x}, \text { if } \mathrm{x} \geq 0 \\ -x, \text { if } \mathrm{x}<0\end{array}\right\}$

$f(-1)=|-1|=1$ and $f(1)=|1|=1$

$\therefore f(-1)=f(1)$ but $-1 \neq 1$

$\therefore f$ is not one-one.

Consider $-1 \in R$

$f(x)=|x|$ is non-negative. There exist any element $x$ in domain $R$ such that $f(x)=|x|=-1$

$\therefore f$ is not onto.

The modulus function is neither one-one nor onto.

Question 5:Show that the signum function $f: R \rightarrow R$ given by onto.

$f(x)=\left\{\begin{array}{c} 1, \text { if } x>0 \\ 0, \text { if } x=0 \\ -1, \text { if } x<0 \end{array}\right\}\text{ is neither one-one nor }$

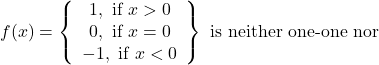
Solution: 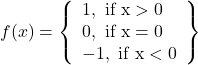$f(x)=\left\{\begin{array}{l} 1, \text { if } \mathrm{x}>0 \\ 0, \text { if } \mathrm{x}=0 \\ -1, \text { if } \mathrm{x}<0 \end{array}\right\}$

$f(1)=f(2)=1$ , but $1 \neq 2$

$\therefore f$ is not one-one.

$f(x)$ takes only 3 values $(1,0,-1)$ for the element $-2$ in co-domain

$\mathrm{R}$ , there does not exist any $x$ in domain $\mathrm{R}$ such that $f(x)=-2$ .

$\therefore f$ is not onto.

The signum function is neither one-one nor onto.

Question 6: Let $A=\{1,2,3\}, B=\{4,5,6,7\}$ and let $f=\{(1,4),(2,5),(3,6)\}$ be a function from $A$ to B. Show that $\mathrm{f}$ is one-one.

Solution: $A=\{1,2,3\}, B=\{4,5,6,7\}$

$f: A \rightarrow B$ is defined as $f=\{(1,4),(2,5),(3,6)\}$

$\therefore f(1)=4, f(2)=5, f(3)=6$

It is seen that the images of distinct elements of $A$ under $f$ are distinct.

$\therefore f$ is one-one.

Question 7: In each of the following cases, state whether the function is one-one, onto or bijective.

Justify your answer.

i). $\quad f: R \rightarrow R$ defined by $f(x)=3-4 x$

ii). $f: R \rightarrow R$ defined by $f(x)=1+x^{2}$

Solution: i. $f: R \rightarrow R$ defined by $f(x)=3-4 x$

$x_{1}, x_{2} \in R$ such that $f\left(x_{1}\right)=f\left(x_{2}\right)$

$\Rightarrow 3-4 x_{1}=3-4 x_{2}$

$\Rightarrow-4 x=-4 x_{2}$

$\Rightarrow x_{1}=x_{2}$

$\therefore f$ is one-one.

For any real number $(y)$ in $R$ , there exists $\frac{3-y}{4}$ in $R$ such that $f\left(\frac{3-y}{4}\right)=3-4\left(\frac{3-y}{4}\right)=y$

$\therefore f$ is onto.

Hence, $f$ is bijective.

ii. $f: R \rightarrow R$ defined by $f(x)=1+x^{2}$

$x_{1}, x_{2} \in R$ such that $f\left(x_{1}\right)=f\left(x_{2}\right)$

$\Rightarrow 1+x_{1}^{2}=1+x_{2}^{2}$

$\Rightarrow x_{1}^{2}=x_{2}^{2}$

$\Rightarrow x_{1}=\pm x_{2}$

$\therefore f\left(x_{1}\right)=f\left(x_{2}\right)$ does not imply that $x_{1}=x_{2}$

Consider $f(1)=f(-1)=2$

$\therefore f$ is not one-one.

Consider an element $-2$ in co domain $R$ .

It is seen that $f(x)=1+x^{2}$ is positive for all $x \in R$ .

$\therefore f$ is not onto.

Hence, $f$ is neither one-one nor onto.

Question 8: Let $A$ and $B$ be sets. Show that $f: A \times B \rightarrow B \times A$ such that $(a, b)=(b, a)$ is a bijective function.

Solution: $f: A \times B \rightarrow B \times A$ is defined as $(a, b)=(b, a)$ .

$\left(a_{1}, b_{1}\right),\left(a_{2}, b_{2}\right) \in A \times B_{\text {such that }} f\left(a_{1}, b_{1}\right)=f\left(a_{2}, b_{2}\right)$ $\Rightarrow\left(b_{1}, a_{1}\right)=\left(b_{2}, a_{2}\right)$

$\Rightarrow b_{1}=b_{2}$ and $a_{1}=a_{2}$

$\Rightarrow\left(a_{1}, b_{1}\right)=\left(a_{2}, b_{2}\right)$

$\therefore f$ is one-one.

$(b, a) \in B \times A$ there exist $(a, b) \in A \times B$ such that $f(a, b)=(b, a)$

$\therefore f$ is onto.

f is bijective.

Question 9: Let $f: N \rightarrow N$ be defined as

$f(n)=\left\{\begin{array}{l} \frac{n+1}{2}, \text { if } n \text { is odd } \\ \frac{n}{2}, \text { if } n \text { is even } \end{array}\right\}$
for all $n \in N$ .

State whether the function $f$ is bijective. Justify your answer.

Solution: $f: N \rightarrow N$ be defined as

$f(n)=\left\{\begin{array}{l} \frac{n+1}{2}, \text { if } n \text { is odd } \\ \frac{n}{2}, \text { if } n \text { is even } \end{array}\right\} \text { for all } n \in N .$

$f(1)=\frac{1+1}{2}=1$ and $f(2)=\frac{2}{2}=1$

$f(1)=f(2)$ , where $1 \neq 2$

$\therefore f$ is not one-one.

Consider a natural number $n$ in co domain $N$ .

Case I: $n$ is odd

$\therefore n=2 r+1$ for some $r \in N$ there exists $4 r+1 \in N$ such that

$f(4 r+1)=\frac{4 r+1+1}{2}=2 r+1$

Case II: $n$ is even

$\therefore n=2 r$ for some $r \in N$ there exists $4 r \in N$ such that

$f(4 r)=\frac{4 r}{2}=2 r$

$\therefore f$ is onto.

$f$ is not a bijective function.

Question 10: Let $A=R-\{3\}, B=R-\{1\}$ and $f: A \rightarrow B$ defined by $f(x)=\left(\frac{x-2}{x-3}\right)$ . Is $f$ one-one and onto? Justify your answer.

Solution: $A=R-\{3\}, B=R-\{1\} \text { and } f: A \rightarrow B \text { defined by } f(x)=\left(\frac{x-2}{x-3}\right)$
$x, y \in A \text { such that } f(x)=f(y)$
$\Rightarrow \frac{x-2}{x-3}=\frac{y-2}{y-3}$
$\Rightarrow(x-2)(y-3)=(y-2)(x-3)$
$\Rightarrow x y-3 x-2 y+6=x y-3 y-2 x+6$
$\Rightarrow-3 x-2 y=-3 y-2 x$
$\Rightarrow 3 x-2 x=3 y-2 y$
$\Rightarrow x=y$

$\therefore f$ is one-one.

Let $y \in B=R-\{1\}$ , then $y \neq 1$

The function $f$ is onto if there exists $x \in A$ such that $f(x)=y$ .

Now,

$\begin{array}{ll} & f(x)=y \\ \Rightarrow & \frac{x-2}{x-3}=y \\ \Rightarrow & x-2=x y-3 y \\ \Rightarrow & x(1-y)=-3 y+2 \\ \Rightarrow & x=\frac{2-3 y}{1-y} \in A \quad[y \neq 1] \end{array}$

Thus, for any $y \in B$ , there exists $\frac{2-3 y}{1-y} \in A$ such that

$f\left(\frac{2-3 y}{1-y}\right)=\frac{\left(\frac{2-3 y}{1-y}\right)-2}{\left(\frac{2-3 y}{1--y}\right)-3}=\frac{2-3 y-2+2 y}{2-3 y-3+3 y}=\frac{-y}{-1}=y$

$\therefore f$ is onto.

Hence, the function is one-one and onto.

Question 11: Let $f: R \rightarrow R$ defined as $f(x)=x^{4}$ .Choose the correct answer.
A. $f$ is one-one onto
B. $f$ is many-one onto
C. $f$ is one-one but not onto
D. $f$ is neither one-one nor onto

Solution: $f: R \rightarrow R$ defined as $f(x)=x^{4}$

$x, y \in R\text { such that } f(x)=f(y)$

$\Rightarrow x^{4}=y^{4}$

$\Rightarrow x=\pm y$

$\therefore f(x)=f(y)$ does not imply that $x=y$ .

For example $f(1)=f(-1)=1$

$\therefore f$ is not one-one.

Consider an element 2 in co domain $R$ there does not exist any $x$ in domain $R$ such that $f(x)=2$ .

$\therefore f$ is not onto.

Function $f$ is neither one-one nor onto.

The correct answer is D.

Question 12: Let $f: R \rightarrow R$ defined as $f(x)=3 x$ .Choose the correct answer.
A. $f$ is one-one onto
B. $f$ is many-one onto
C. $f$ is one-one but not onto
D. $f$ is neither one-one nor onto

Solution: $f: R \rightarrow R$ defined as $f(x)=3 x$

$x, y \in R_{\text {such that }} f(x)=f(y)$

$\Rightarrow 3 x=3 y$

$\Rightarrow x=y$ $\therefore f$ is one-one.

For any real number $y$ in co domain $\mathrm{R}$ , there exist $\frac{y}{3}$ in $\mathrm{R}$ such that $f\left(\frac{y}{3}\right)=3\left(\frac{y}{3}\right)=y$

$\therefore f$ is onto.

Hence, function $f$ is one-one and onto.

The correct answer is A.

Exercise 1.2

Leave a Comment Cancel reply