Chapter 2 Miscellaneous(Sets) Class 11

Question 1: The relation f is defined by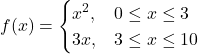

 The relation g is defined by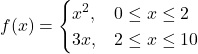 

 Show that f is a function and g is not a function.

Solution: The given relation f is defined as:

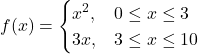
It is seen that for 0 ≤ x < 3,

f(x) = x² and for 3 < x ≤ 10,

f(x) = 3x

Also, at x = 3

f(x) = 3² = 9 or f(x) = 3 × 3 = 9

i.e., at x = 3, f(x) = 9 [Single image]

Hence, for 0 ≤ x ≤ 10, the images of f(x) are unique.

Therefore, the given relation is a function.

Now,

In the given relation, g is defined as

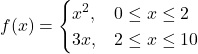
It is seen that, for x = 2

g(x) = 2² = 4 and g(x) = 3 × 2 = 6

Thus, element 2 of the domain of the relation g corresponds to two different images, i.e., 4 and 6.

Therefore, this relation is not a function.

Question 2: If f(x) = x², find

Solution: Given, f(x) = x²

Hence,

Question 3: Find the domain of the function 

Solution: Given function,

It’s clearly seen that the function f is defined for all real numbers except at x = 6 and x = 2, as the denominator becomes zero otherwise.

Therefore, the domain of f is R – {2, 6}.

Question 4: Find the domain and the range of the real function f defined by f(x) = √(x – 1).

Solution: Given real function,

f(x) = √(x – 1)

Clearly, √(x – 1) is defined for (x – 1) ≥ 0

So, the function f(x) = √(x – 1) is defined for x ≥ 1

Thus, the domain of f is the set of all real numbers greater than or equal to 1.

Domain of f = [1, ∞)

Now,

As x ≥ 1 ⇒ (x – 1) ≥ 0 ⇒ √(x – 1) ≥ 0

Thus, the range of f is the set of all real numbers greater than or equal to 0.

Range of f = [0, ∞)

Question 5: Find the domain and the range of the real function f defined by f (x) = |x – 1|.

Solution: Given a real function,

f (x) = |x – 1|

Clearly, the function |x – 1| is defined for all real numbers.

Hence,

Domain of f = R

Also, for x ∈ R, |x – 1| assumes all real numbers.

Therefore, the range of f is the set of all non-negative real numbers.

Question 6: Let be a function from R into R. Determine the range of f.

Solution: Given function,

Substituting values and determining the images, we have

The range of f is the set of all second elements. It can be observed that all these elements are greater than or equal to 0 but less than 1.

[As the denominator is greater than the numerator.]

Or,

We know that, for x ∈ R,

x² ≥ 0

Then, x² + 1 ≥ x²

1 ≥ x² / (x² + 1)

Therefore, the range of f = [0, 1)

Question 7: Let f, g: R → R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and f/g.

Solution: Given the functions f, g: R → R is defined as

f(x) = x + 1, g(x) = 2x – 3

Now,

(f + g) (x) = f(x) + g(x) = (x + 1) + (2x – 3) = 3x – 2

Thus, (f + g) (x) = 3x – 2

(f – g) (x) = f(x) – g(x) = (x + 1) – (2x – 3) = x + 1 – 2x + 3 = – x + 4

Thus, (f – g) (x) = –x + 4

(f/g)(x) = f(x)/g(x), g(x) ≠ 0, x ∈ R

(f/g)(x) = x + 1/ 2x – 3, 2x – 3 ≠ 0

Thus,( f/g)(x) = x + 1/ 2x – 3, x ≠ 3/2

Question 8: Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.

Solution: Given, f = {(1, 1), (2, 3), (0, –1), (–1, –3)}

And the function defined as,  f(x) = ax + b

For (1, 1) ∈ f

We have,  f(1) = 1

So, a × 1 + b = 1

a + b = 1 …. (i)

And for (0, –1) ∈ f

We have f(0) = –1

a × 0 + b = –1

b = –1

On substituting b = –1 in (i), we get

a + (–1) = 1 ⇒ a = 1 + 1 = 2.

Therefore, the values of a and b are 2 and –1, respectively.

Question 9: Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b²}. Are the following true?

(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R

(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R

Justify your answer in each case.

Solution: Given relation R = {(a, b): a, b ∈ N and a = b²}

(i) It can be seen that 2 ∈ N; however, 2 ≠ 2² = 4.

Thus, the statement “(a, a) ∈ R, for all a ∈ N” is not true.

(ii) Its clearly seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 3².

Now, 3 ≠ 9² = 81; therefore, (3, 9) ∉ N

Thus, the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.

(iii) It’s clearly seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 4² and 4 = 2².

Now, 16 ≠ 2² = 4; therefore, (16, 2) ∉ N

Thus, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.

Question 10: Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?

(i) f is a relation from A to B (ii) f is a function from A to B

Justify your answer in each case.

Solution: Given,

A = {1, 2, 3, 4} and B = {1, 5, 9, 11, 15, 16}

So,

A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11), (3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}

Also, given that,

f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}

(i) A relation from a non-empty set A to a non-empty set B is a subset of the Cartesian product A × B.

It’s clearly seen that f is a subset of A × B.

Therefore, f is a relation from A to B.

(ii) As the same first element, i.e., 2 corresponds to two different images (9 and 11), relation f is not a function.

Question 11: Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.

Solution: Given relation, f is defined as

f = {(ab, a + b): a, b ∈ Z}

We know that a relation f from a set A to a set B is said to be a function if every element of set A has unique images in set B.

As 2, 6, –2, –6 ∈ Z, (2 × 6, 2 + 6), (–2 × –6, –2 + (–6)) ∈ f

i.e., (12, 8), (12, –8) ∈ f

It’s clearly seen that the same first element, 12, corresponds to two different images (8 and –8).

Therefore, the relation f is not a function.

Question 12: Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.

Solution: Given,

A = {9, 10, 11, 12, 13}

Now, f: A → N is defined as

f(n) = The highest prime factor of n

So,

Prime factor of 9 = 3

Prime factors of 10 = 2, 5

Prime factor of 11 = 11

Prime factors of 12 = 2, 3

Prime factor of 13 = 13

Thus, it can be expressed as

f(9) = The highest prime factor of 9 = 3

f(10) = The highest prime factor of 10 = 5

f(11) = The highest prime factor of 11 = 11

f(12) = The highest prime factor of 12 = 3

f(13) = The highest prime factor of 13 = 13

The range of f is the set of all f(n), where n ∈ A.

Therefore,

Range of f = {3, 5, 11, 13}

 

Ex 2.3 sets ncert maths solution class 11