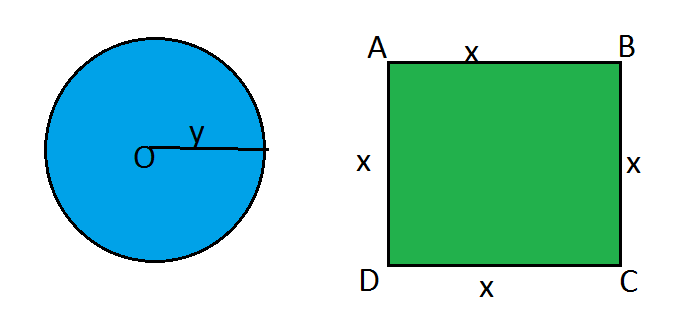
A wire of length 28 m is to be cut into two pieces

15/02/2023 by Team Gmath

Question: A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?

Solution: Let $\mathrm{x}$ meters be the side of square and $y$ meters be the radius of the circle.

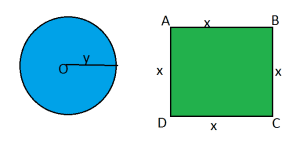
Length of the wire = Perimeter of square + Circumference of circle

$4 x+2 \pi y=28$

$\Rightarrow 2 x+\pi y=14$

$\Rightarrow y=\frac{14-2 x}{\pi}$

$\text { Area of square }=x^2, \text { and Area of circle }=\pi y^2$

$\text { Combined area }(\mathrm{A})=x^2+\pi y^2=x^2+\pi\left(\frac{14-2 x}{\pi}\right)^2$

$=x^2+\frac{4}{\pi}(7-x)^2$

$d\frac{dA}{d x}=2 x-\dfrac{8}{\pi}(7-x) \text { and }$

$\dfrac{d^2 A}{d x^2}=2+\dfrac{8}{\pi}$

Now For max and minima $\dfrac{d A}{d x}=0$

$2 x-\dfrac{8}{\pi}(7-x)=0$

$\Rightarrow 2 x=\dfrac{8}{\pi}(7-x)$

$\Rightarrow 2 \pi x=56-8 x$

$\Rightarrow (2 \pi+8) x=56$

$\Rightarrow x=\dfrac{56}{2 \pi+8}=\dfrac{28}{\pi+4}$

$\text { And } \dfrac{d^2 A}{d x^2}=2+\dfrac{8}{\pi} \text { [Positive] }$

$\text { A is minimum when } x=\dfrac{28}{\pi+4}$

Therefore, the length of one piece = $4 x=\dfrac{112}{\pi+4}$

Length of second piece $= 2\pi y= 28- \dfrac{28}{\pi+4}$

$= \dfrac{28\pi+112-112}{28+\pi}$

$= \dfrac{28\pi}{28+\pi}$

class 12 maths ex 6.5 ncert solution

Leave a Comment Cancel reply