Chapter 4:Quadratic Equation

Class 10 Case based problem of Chapter 4 quadratic eq 1

Class 10 Case based problem of Chapter 4 Quadratic eq 2

Case Based: 1

A ship is sailing very close to a light house and a right angle triangle is formed by the light house, line joining the ship to the base of the light house. At a particular instant, the hypotenuse of the right angle triangle so formed is 4 m more than thrice the shortest side and the third side is 1 m less than the hypotenuse.

Class 10 Case based problem of Chapter 4 quadratic eq 1 — A ship is sailing very close to a light house and a right angle

(A) Taking the length of the shortest side of the triangle as x m, form the quadratic equation of the given situation.

(B) Find length of the shortest side of the right angled triangle formed is .

Solution:

(A) The length of the shortest side of the triangle = x m

Hypotenuse = (3x + 4) m

Third side = (3x + 3) m

From pythagoras theorem

$H^2 = P^2 + B^2$

$\Rightarrow (3x+ 4)^2 = (3x + 3)^2 + x^2$

$\Rightarrow 9x^2 + 16 + 24 x = 9x^2 + 9 + 18 x + x^2$

$\Rightarrow 0 = x^2 +18 x -24 x + 9-16$

$\Rightarrow x^2 - 6x -7 =0$ …….(i)

(B) For shortest distance solving eq (i)

$x^2 - 6x -7=0$

$\Rightarrow x^2 -7x + x -7 = 0$

$\Rightarrow x(x - 7)+1(x - 7) = 0$

$\Rightarrow (x-7)(x+1)=0$

The roots of the equation = 7, -1

The length can not be negative,

Hence, the length of shortest side = x = 7 m.

Case Based: 2

A chess board contains 64 equal squares and the area of each square is 6.25 cm². A border round the board is 3 cm wide.

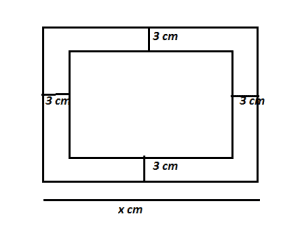
(A) Find the length of the side of the chess board.

(B) If x = 2/3 and x = -3 are roots of the quadratic equation a x² + 7 x + b = 0, find the values of a and b.

Solution:

(A) The number of small square = 64

The area of each square = 6.25 cm²

Therefore, area of chess board = 64×6.25 cm² = 400 cm²

Let the length of each side of the chess board = x cm.

Side of inner square = x – 3×2

= x – 6

Width of the boarder = 3 cm.

From the question

(x – 6)² = 400

⇒ x² + 36 – 12 x = 400

⇒ x² – 12x +36 – 400 = 0

⇒ x² – 12x – 364 = 0

⇒ x² – 26x + 14x – 364 =0

⇒ x(x – 26) +14(x – 26) = 0

⇒ (x – 26)(x + 14) =0

⇒ x = 26, -14

Length can not be negative, Length of each side of the chess board = 26 cm.

(B) x = 2/3 and x = -3 are roots of the quadratic equation $ax^2+7x+b = 0$

Putting x = 2/3 in equation

$a(\frac{2}{3})^2+7(\frac{2}{3})+b = 0$

$\Rightarrow \frac{4a}{9} + \frac{14}{3}+b =0$

$\Rightarrow 4a + 9b = -42$ …….(i)

similarly putting x = -3 in equation

$a(-3)^2 + 7(-3) +b =0$

$\Rightarrow 9a - 21 +b =0$

$\Rightarrow b = 21-9a$ ……….(ii)

Replacing in equation (i)

$4a + 9(21 - 9a) = -42$

$\Rightarrow 4a + 189 - 81a = -42$

$\Rightarrow -77a = -42-189$

$\Rightarrow -77a = -231$

$\Rightarrow a = 3$

Substituting the value of a in eq (ii)

$b = 21 - 9\times 3$

$\Rightarrow b = 21 -27= -6$

Case Based : 3

A passenger while boarding a palne slipped from the stairs and got hurt. The pilot took the passenger to the emergency clinic at the airport for treatment. Due to this, plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/h than the usual speed.