EXERCISE 4.5 (Determinant)
class 12 maths exercise 4.5 ncert solution
Question 1: Find the adjoint of the matrix ![]()
Solution: Let![]()
Then,![]()
Thus
![]()
![]()
![]()
Question 2: Find the adjoint of the matrix 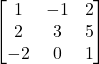
Solution: Let 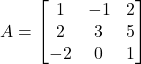
Then,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
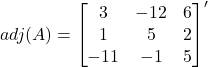

Question 3: Verify ![]() for
for
![]()
Solution: Let ![]()
Then,
![]()
![]()
Also,
![]()
![]()
Now,
![]()
![]()
Hence,
![]()
Now,
![]()
![]()
![]()
Also,
![]()
![]()
![]()
Hence,
![]() .
.
Question 4: verify ![]() for
for
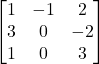
Solution : Let 
Then
![]()
Also,
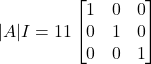

Now,
![]()
![]() `
`
![]()
![]()
![]()
![]()
![]()
![]()
![]()
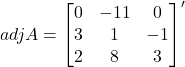
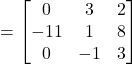
Now,
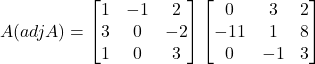
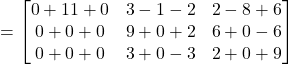

Also,

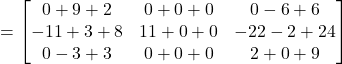

Hence, ![]()
Question 5: Find the inverse of each of the matrix ![]() (if it exist).
(if it exist).
Solution: Let ![]()
Then,
![]()
Now,
![]()
![]()
![]()
![]()
![]()
Question 6: Find the inverse of the matrix ![]() (if it exists)
(if it exists)
Solution: Let ![]()
Then ![]()
Now,
![]()
Therefore,
![]()
![]()
Hence,
![]()
Question 7: Find the inverse of the matrix  (if it exists)
(if it exists)
Solution: Let 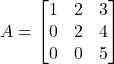
Then,
![]()
Now,
![]()
![]()
![]()
Therefore,
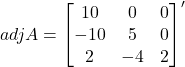

Hence,
![]()
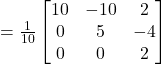
Question 8: Find the inverse of each of the matrix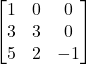 (if it exists)
(if it exists)
Solution: Let 
Then
![]()
Now,
![]()
![]()
![]()
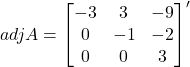
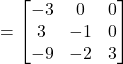
![]()
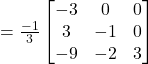
Question 9: Find the inverse of each of the matrix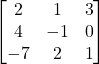 (if it exists)
(if it exists)
Solution: 
Then,
![]()
![]()
Now,
![]()
![]()
![]()
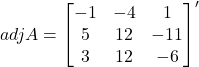

Hence,
![]()
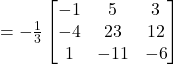
Question 10: Find the inverse of the matrix 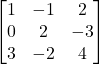 (if it exists).
(if it exists).
Solution: Let 
Then, expanding
![]()
![]()
![]()
Now,
![]()
![]()
![]()
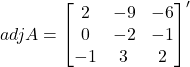
Therefore,
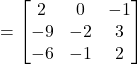
Hence,
![]()
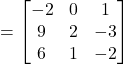
Question 11: Find the inverse of the matrix 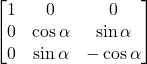 (if it exists)
(if it exists)
Solution: Let 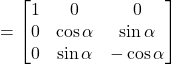
Then,
![]()
![]()
![]()
Now,
![]()
![]()
![]()
Therefore,

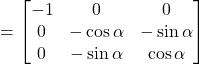
![]()
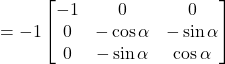
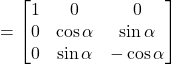
Question 12: Let ![]() and
and ![]() verify that
verify that ![]()
Solution: Let ![]()
Then,
![]()
Now,
![]()
![]()
![]()
![]()
Therefore,
![]()
![]()
Now for B
Let ![]()
Then,
![]()
Now, ![]()
![]()
![]()
![]()
Then,
![]()
![]()
![]()
Now,
![]()
![]()
![]()
Also,
![]()
![]()
![]()
Then we have,
![]()
![]()
and
![]()
![]()
Therefore,
![]()
![]()
Thus,
![]()
![]()
![]()
From (1) and (2),
![]()
Hence, proved.
Question 13: If ![]() , show that
, show that ![]() . Hence find
. Hence find ![]() .
.
Solution: Let ![]()
Therefore,
![]()
![]()
![]()
Now,
![]()
![]()
![]()
![]()
Hence, ![]() .
.
Now,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thus,
![]()
Question 14: For the matrix ![]() , find the numbers
, find the numbers ![]() and
and ![]() such that
such that ![]() .
.
Solution: Let ![]()
Therefore,
![]()
![]()
Now, ![]() .
.
Hence,
![]()
![]()
![]()
![]()
![]()
Now,
![]()
![]()
![]()
From (1) and (2), we have,
![]()
![]()
![]()
Comparing the corresponding elements of the two matrices, we have:
![]()
![]()
Also,
![]()
![]()
![]()
Thus, ![]() and
and ![]() .
.
Question 15: 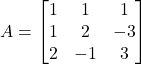
show that
![]()
Hence, find ![]() .
.
Solution: Let 
Therefore,
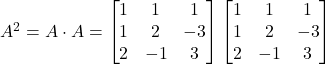

And,
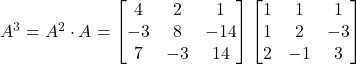

Hence,
![]()

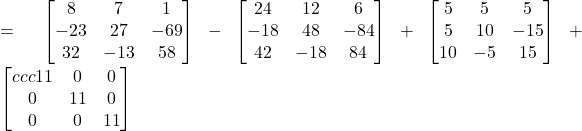


![]()
Thus, ![]()
Now,
![]()
![]()
![]()
![]()
![]()
Now,
![]()

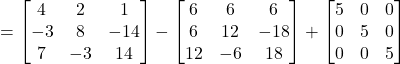

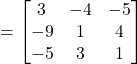
From equation (1) and (2)

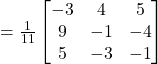
Question 16: If 
verify that
![]() . Hence, find
. Hence, find ![]() .
.
Solution: Let 
Therefore,
![]()
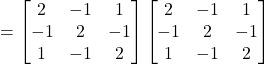

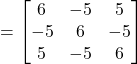
And
![]()

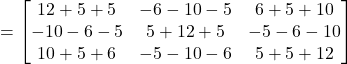
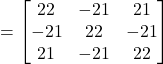
Now,
![]()




![]()
Thus,
![]()
Now,
![]()
![]()
![]()
![]()
![]()
![]()
Now,
![]()



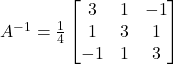
From equations ![]() and
and ![]()
Question 17: Let ![]() be a non-singular square matrix of order
be a non-singular square matrix of order ![]() . Then
. Then ![]() is equal to:
is equal to:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution: the correct option is B.
Since ![]() be a non-singular square matrix of order
be a non-singular square matrix of order ![]()
![]()

Therefore,
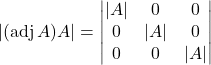
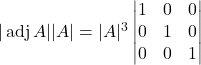
![]()
![]()
Thus, the correct option is B.
Question 18: If ![]() is an invertible matrix of order 2, the
is an invertible matrix of order 2, the ![]() is equal to:
is equal to:
(A) ![]()
(B) ![]()
(C) 1
(D) 0
Solution: Thus, the correct option is B.
Since ![]() is an invertible matrix,
is an invertible matrix, ![]() exists and
exists and ![]() adj
adj ![]() .
.
As matrix ![]() is of order 2, let
is of order 2, let ![]() Then,
Then,
![]()
And
![]()
Now,
![]()
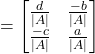
Hence,

![]()
![]()
![]()
![]()
Hence,
![]()
Thus, the correct option is B.


