Multiple choice (Inverse Trigonometry)

choose the correct option in the following question:(class 12 inverse trigonometric functions multiple choice)
Question 1: The value of ![]() corresponding to principal branches is
corresponding to principal branches is
(a) -π/12 (b) 0
(c) π (d) π/3
Answer (c)
Explanation: ![]()
![]()
![]()
![]()
![]()
Question 2: The value of ![]() is
is
(a) ![]() (b)
(b) ![]()
(c) 1/x (d) ![]()
Answer (d)
Explanation: ![]()
Let ![]()
![]()
![]()
![]()
![]()
![]()
Since, ![]()
![]()
![]()
![]()
![]()
Question 3: The value of ![]() is
is
(a) π/9 (b) 5π/9
(c) -5π/9 (d) 7π/18
Answer (d)
Explanation: ![]()
![]()
![]()
Question 4: Let ![]() , Then value of θ is
, Then value of θ is
(a) π/3 (b) π/2
(c) 2π/3 (d) – 2π/3
Answer (a)
Explanation: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 5: The principal value of ![]() is
is
(a) 2π/5 (b) -2π/5
(c) 3π/5 (d) -3π/5
Answer: (b) -2π/5
Explanation: ![]()
![]()
![]() {since
{since ![]() }
}
= –![]()
= –2π/5
Question 6: ![]() is equal to:
is equal to:
(a) 1/2 (b) 1/3
(c) -1 (d) 1
Answer: (d) 1
Explanation: ![]()
![]()
= sin[π/3 – (-π/6)]
= sin(π/3 + π/6)
= sin (π/2)
= 1
Question 7: The domain of ![]() is
is
(a) [0, 1] (b) [– 1, 1]
(c) [-1/2, 1/2] (d) [–2, 2]
Answer: (c) [-1/2, 1/2]
Explanation: Let, ![]() .
.
![]() 2x = sin θ.
2x = sin θ.
Since, – 1 ≤ sin θ ≤ 1
![]() – 1 ≤ 2x ≤ 1\Rightarrow
– 1 ≤ 2x ≤ 1\Rightarrow![]() \sin^{-1}(2x)
\sin^{-1}(2x)![]() \sin^{–1}x + \sin^{–1}y = \pi/2
\sin^{–1}x + \sin^{–1}y = \pi/2![]() \cos^{–1}x + \cos^{–1}y
\cos^{–1}x + \cos^{–1}y \sin^{–1} x + \sin^{–1} y = \pi/2\Rightarrow [(\pi/2) – \cos^{-1}x] + [(\pi/2) – \cos^{-1}y] = \pi/2
\sin^{–1} x + \sin^{–1} y = \pi/2\Rightarrow [(\pi/2) – \cos^{-1}x] + [(\pi/2) – \cos^{-1}y] = \pi/2![]() \cos^{-1}x + \cos^{-1}y
\cos^{-1}x + \cos^{-1}y![]() \cos^{-1}x + \cos^{-1}y
\cos^{-1}x + \cos^{-1}y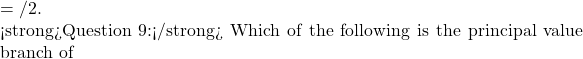 \cos^{–1}x
\cos^{–1}x![Rendered by QuickLaTeX.com ? (a) [-π/2, π/2] (b) (0, π) (c) [0, π] (d) (0, π) - {π/2} <strong>Answer: (c) [0, π]</strong> Explanation: The principal value branch of](https://gmath.in/wp-content/ql-cache/quicklatex.com-e9403ffaf588dfd81900b31bf6f7effd_l3.png) \cos^{-1}x
\cos^{-1}x![]() \sin [\cot^{–1} (\cos (\tan^{–1} 1))]
\sin [\cot^{–1} (\cos (\tan^{–1} 1))] \sin [\cot^{–1} (\cos (\tan^{–1} 1))]
\sin [\cot^{–1} (\cos (\tan^{–1} 1))]![]() \sin [\cot^{–1} (\cos (\tan^{–1} (\tan \pi/4))]
\sin [\cot^{–1} (\cos (\tan^{–1} (\tan \pi/4))]![]() = \sin[\cot^{-1} (\cos \pi/4)]= \sin[\cot^{-1}(1/√2)]= \sin [\sin^{-1}(√(⅔))]
= \sin[\cot^{-1} (\cos \pi/4)]= \sin[\cot^{-1}(1/√2)]= \sin [\sin^{-1}(√(⅔))]![]() y = \cos^{–1} (x^2 – 4)
y = \cos^{–1} (x^2 – 4)![Rendered by QuickLaTeX.com is (a) [3, 5] (b) [0, π] (c) [-√5, -√3] ∩ [-√5, √3] (d) [-√5, -√3] ∪ [√3, √5] <strong>Answer: (d)</strong> <strong>Explanation:</strong> Given,](https://gmath.in/wp-content/ql-cache/quicklatex.com-16198ce15d472bf3a34d726342ea0e16_l3.png) y = \cos^{–1} (x^2 – 4 )\Rightarrow \cos y = x^2 – 4
y = \cos^{–1} (x^2 – 4 )\Rightarrow \cos y = x^2 – 4![]() x^2 – 4
x^2 – 4![]() x^2
x^2![Rendered by QuickLaTeX.com \le 5 ⇒ √3 \le x \le √5 ⇒ x∈ [-√5, -√3] ∪ [√3, √5] <strong>Question 12:</strong> If α \le](https://gmath.in/wp-content/ql-cache/quicklatex.com-3e95fd6472dcb572c00f1c6eb57b5e11_l3.png) 2 \sin^{–1}x + \cos^{–1}x
2 \sin^{–1}x + \cos^{–1}x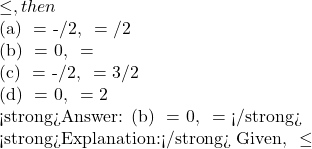 2 \sin^{–1}x + \cos^{–1}x
2 \sin^{–1}x + \cos^{–1}x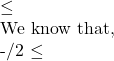 \sin^{–1}
\sin^{–1}![]() \sin^{–1}x
\sin^{–1}x![]() \sin^{–1}x + (\sin^{–1}x + \cos^{–1}x)
\sin^{–1}x + (\sin^{–1}x + \cos^{–1}x)![]() 2 \sin^{–1}x + \cos{–1}x
2 \sin^{–1}x + \cos{–1}x![]() 2 \sin^{–1}x + \cos{–1}x
2 \sin^{–1}x + \cos{–1}x![]() \sin (2 \tan^{–1} (.75))
\sin (2 \tan^{–1} (.75))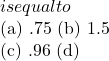 \sin 1.5
\sin 1.5![]() \sin (2\tan^{–1} (.75))
\sin (2\tan^{–1} (.75))![]() \tan^{–1} (.75)
\tan^{–1} (.75)![]() \Rightarrow \tan \theta = 0.75\Rightarrow \tan \theta = 3/4
\Rightarrow \tan \theta = 0.75\Rightarrow \tan \theta = 3/4![]() \sin (2\tan^{–1} (.75)) = \sin 2θ\theta
\sin (2\tan^{–1} (.75)) = \sin 2θ\theta![]() tan^{-1}(.75) = \theta
tan^{-1}(.75) = \theta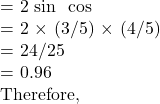 \sin (2\tan^{–1} (.75)) = .96
\sin (2\tan^{–1} (.75)) = .96![]() \sin(\tan^{-1} x)
\sin(\tan^{-1} x)![]() x/√(1 – x^2)
x/√(1 – x^2)![]() 1/√(1 – x^2)
1/√(1 – x^2)![]() 1/√(1 + x^2)
1/√(1 + x^2)![]() x/√(1 + x^2)
x/√(1 + x^2)![]() x/√(1 + x^2)
x/√(1 + x^2)![]() \tan^{-1}x =
\tan^{-1}x =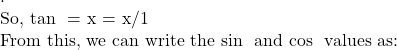 \sin \theta = x/√(1 + x^2)\cos \theta = 1/√(1 + x^2)
\sin \theta = x/√(1 + x^2)\cos \theta = 1/√(1 + x^2)![]() \sin(\tan^{-1} x) = \sin \theta = x/√(1 + x^2)
\sin(\tan^{-1} x) = \sin \theta = x/√(1 + x^2)![]() 2\sec^{-1}2+\sin^{-1}(\frac{1}{2})
2\sec^{-1}2+\sin^{-1}(\frac{1}{2}) 2\sec^{-1}2+\sin^{-1}(\frac{1}{2})= \frac{2\pi}{3} + \frac{\pi}{6}=\frac{5\pi}{6}
2\sec^{-1}2+\sin^{-1}(\frac{1}{2})= \frac{2\pi}{3} + \frac{\pi}{6}=\frac{5\pi}{6}![]() \tan^2(\sec^{-1}2) +\cot^2(\opratorname{cosec}^{-1}3)
\tan^2(\sec^{-1}2) +\cot^2(\opratorname{cosec}^{-1}3) f(x) =\sin^{-1}\sqrt{1-x}
f(x) =\sin^{-1}\sqrt{1-x}![Rendered by QuickLaTeX.com is (a) [1, 2] (b) [-1, 1] (c) [0, 1] (d) None of these <strong>Answer (a)</strong> <strong>Question 18: The value of</strong>](https://gmath.in/wp-content/ql-cache/quicklatex.com-a4d238429c117e6df1edacd1182f74ec_l3.png) \cot[\cos^{-1}(\frac{7}{25})]
\cot[\cos^{-1}(\frac{7}{25})]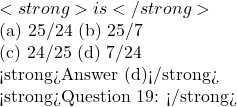 \sin(\tan^{-1}x), |x|<1
\sin(\tan^{-1}x), |x|<1![]() \frac{x}{\sqrt{1-x^2}}
\frac{x}{\sqrt{1-x^2}}![]() \frac{1}{\sqrt{1-x^2}}
\frac{1}{\sqrt{1-x^2}}![]() \frac{1}{\sqrt{1+x^2}}
\frac{1}{\sqrt{1+x^2}}![]() \frac{x}{\sqrt{1+x^2}}
\frac{x}{\sqrt{1+x^2}}![]() \cos^{-1}\alpha+\cos^{-1}\beta+\cos^{-1}\gamma = 3\pi
\cos^{-1}\alpha+\cos^{-1}\beta+\cos^{-1}\gamma = 3\pi![]() \alpha(\beta +\gamma)+\beta(\gamma+\alpha)+\gamma(\alpha+\beta)
\alpha(\beta +\gamma)+\beta(\gamma+\alpha)+\gamma(\alpha+\beta) \cos^{-1}x
\cos^{-1}x![Rendered by QuickLaTeX.com ? (a) [-π/2, π/2] (b) (0, π) (c) [0, π] (d) (o, π) - {π/2} <strong>Answer (c)</strong> <strong>Question 22: The value of </strong>](https://gmath.in/wp-content/ql-cache/quicklatex.com-16abe44370bfeb437289aee88bc0c212_l3.png) \sin^{-1}[\cos(33π/5)]
\sin^{-1}[\cos(33π/5)] \cos^{-1}(2x-1)
\cos^{-1}(2x-1)![Rendered by QuickLaTeX.com is (a) [0, 1] (b) [-1, 1] (c) (-1, 1) (c) [0, π] <strong>Answer (a)</strong> <strong>Question 24:Which of the following is the principal value branch of</strong>](https://gmath.in/wp-content/ql-cache/quicklatex.com-728ca7bf748d33ecac1defc21b97af71_l3.png) \operatorname{cosec}^{-1}x
\operatorname{cosec}^{-1}x![Rendered by QuickLaTeX.com ? (a) ( -π/2, π/2) (b) (0, π) - { π/2} (c) {- π/2, π/2} (d) [- π/2, π/2] - {0} <strong>Answer (d)</strong> <strong>Question 25: If</strong>](https://gmath.in/wp-content/ql-cache/quicklatex.com-d82622104e4e3ed94ed74eeaa536cfca_l3.png) \cos(\sin^{-1}\frac{3}{5}+\cos^{-1})= 0
\cos(\sin^{-1}\frac{3}{5}+\cos^{-1})= 0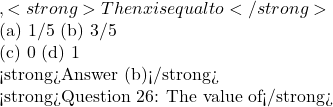 \cos^{-1}(2x^2-1),0 \leq x\lea 1
\cos^{-1}(2x^2-1),0 \leq x\lea 1![]() 2\cos^{-1}x
2\cos^{-1}x![]() \sin^{-1}x
\sin^{-1}x![]() \pi – 2\cos^{-1}x
\pi – 2\cos^{-1}x![]() \pi + 2\cos^{-1}x
\pi + 2\cos^{-1}x![]() \sqrt{1+\cos 2x} = \sqrt{2}\cos^{-1}(\cos x)
\sqrt{1+\cos 2x} = \sqrt{2}\cos^{-1}(\cos x)![Rendered by QuickLaTeX.com in [ π/2, π] is (a) 0 (b) 1 (c) 2 (d) ∞ <strong>Answer (a)</strong> <strong>Question 28: The value of</strong>](https://gmath.in/wp-content/ql-cache/quicklatex.com-dfa4961546eb0b447cab8c92349ee8eb_l3.png) 2\cos^{-1}(\frac{-1}{2})+2\sin^{-1}(\frac{-1}{2})-\cos^{-1}(-1)
2\cos^{-1}(\frac{-1}{2})+2\sin^{-1}(\frac{-1}{2})-\cos^{-1}(-1)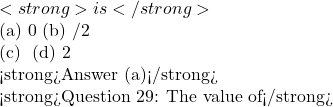 \cot[\frac{1}{2}\sin^{-1}\frac{\sqrt{3}}{2}]
\cot[\frac{1}{2}\sin^{-1}\frac{\sqrt{3}}{2}]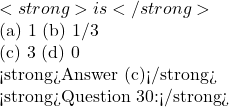 \sin(\cot^{-1}x)
\sin(\cot^{-1}x)![]() \sqrt{1+x^2}
\sqrt{1+x^2}![]() (1+x^2)^{-3/2}
(1+x^2)^{-3/2}![]() (1+x^2)^{-1/2}$
(1+x^2)^{-1/2}$
Answer (d)

