Class 10 Case based problem of Chapter 6 Triangles 1

Class 10 Case based problem of Chapter 6 Triangles 2

Case study:1

While browsing through the catalogue of wooden shelves. Ravi came across this beautiful triangular shaped shelf. A shelf DE parallel to the base BC could be used for displaying small plants and showpieces

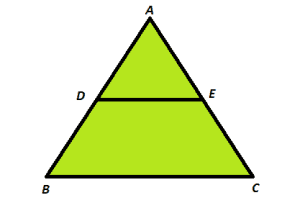
(A) Find the relation between the sides AD, DB, AE and EC. Also, mention the theorem used .

(B) Find the volue of x if AD = (x + 3) cm, BD = (3x + 19) cm, AE = x cm and EC = (3x + 4) cm.

Solution:

(A) Since DE is parallel to BC. So by Basic Proportionality theorem

$\dfrac{AD}{BD} = \dfrac{AE}{CE}$

(B) Since, AD = (x + 3) cm, BD = (3x + 19) cm, AE = x cm and EC = (3x + 4) cm

From (A)

$\dfrac{AD}{BD} = \dfrac{AE}{CE}$

$\Rightarrow \dfrac{x + 3}{3x + 19} = \dfrac{x}{3x + 4}$

$\Rightarrow (x + 3)(3x + 4) = x (3x + 19)$

$\Rightarrow 3x^2 + 4x + 9x + 12 = 3x^2 + 19x$

$\Rightarrow 13x - 19x + 12 = 0$

$\Rightarrow -6x + 12 =0$

$\Rightarrow x = 2$

Case study : 2

The Louvre Pyramid(Pyramide du Louvre) is a large glass and metal pyramid designed by Chinese- American architect I.M. pei, surrounded by three smaller pyramids, in the main courtyard(Cour Napoleon) of the Louvre Palace (Palace du Louvre) in Paris. The large pyramid serves as the main entrance to the Louvre Museum. Completed in 1989, it has become a landmark of the city of Paris. As can be seen, two triangles ΔABC and ΔDEF have been marked in the image. Where DE||AB and EF||BC.

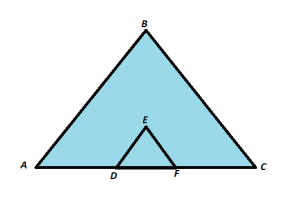
(A) Which axiom is used in proving similarity of triangles ΔABC and ΔDEF ? Further, if the measures of sides AB, BC and DE are 15 m, 21 m and 10 m respectively, then find measure of side EF.

(B) In relation to the part(A), find the ratio of sides DF : AC

Solution:

(A) Given that DE||AB and EF||BC

And DF||AE

So, ΔDEF ∼ ΔABC (by SSS)

Hence,

$\dfrac{DE}{AB} = \dfrac{EF}{BC}$

AB = 15 m, BC = 21 m and DE = 10 m

$\Rightarrow \dfrac{10}{15} =\dfrac{EF}{21}$

$\Rightarrow \dfrac{2}{5}=\dfrac{EF}{21}$

$\Rightarrow EF = \dfrac{21 \times 2}{5}=8.4$ m

(B) From Part (A)

$\dfrac{DF}{AC} = \dfrac{DE}{AB}$

$\Rightarrow \dfrac{DF}{AC} = \dfrac{10}{15}$

$\Rightarrow DF : AC = 2 : 5$

Case Study :3

Rahul is studying in Xth Standard . He is making a kite to fly it on sunday. Few questions came to his mind while making the kite . Give answers to his questions by looking at the figure.

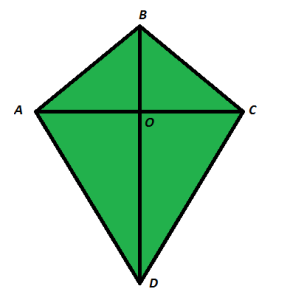
(A) Rahul tied the sticks at what angles to each other ?

(a) 30° (b) 60°

(B) Which is the correct similarity criteria applicate for smaller triangles at the upper part of the kite ?

(a) RHS (b) SAS

(C) Sides of two similar trianglres are in the ratio 4 : 9. Corresponding medians of thes triangles are in the ratio:

(a) 2 : 3 (b) 4 : 9

(D) What is the area of the kite , formed by two perpendicular stick of length 6 cm and 8 cm ?

(a) 48 square cm (b) 14 square cm

(E) In a triangle, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points the other two sides are divided in the same ratio. This theorem is called as:

(a) Pythagoras theorem

(b) Thales theorem

(d) Converse of pythagoras theorem