Prove that the volume of the largest cone that can be inscribed in a sphere

Prove that the volume of the largest cone that can be

by

Question: Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 8/27 of the volume of the sphere.

Solution: Consider O be the centre and R be the radius of the given sphere, O M=x

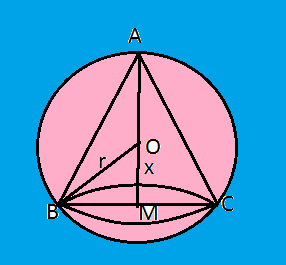
Prove that the volume of the largest cone that can be inscribed in a sphere

In ΔOBM, using pythagoras theorem

OB^2=OM^2+BM^2

\Rightarrow R^2 = x^2 + BM^2

\Rightarrow BM^2 = R^2-x^2

AM= h = R+x

BM is the radius of cone

Volume of cone V = \frac{1}{3}\pi r^2 h

\Rightarrow V = \frac{1}{3}\pi(R^2-x^2)(R+x)--(i)

\Rightarrow V = \frac{1}{3}\pi(R-x)(R+x)(R+x)

\Rightarrow V = \frac{1}{3}\pi (R-x)(R+x)^2

Differentiating with respect to x

\frac{dV}{dx} = \frac{1}{3}\pi [(R-x)2(R+x)+(R+x)^2(-1)]

= \frac{1}{3}\pi (R+x)[2(R-x)-(R+x)]

= \frac{1}{3}\pi(R+x)[2R-2x-R-x]

=\frac{1}{3}\pi (R+x)[R-3x]—(ii)

For max and minima \frac{dV}{dx}=0

\frac{1}{3}\pi (R+x)[R-3x]=0

Hence R+x=0 or R-3x = 0

x = -R or x = R/3

x =-R Not possible

Agian differentiate with respect to x of eq (ii)

\frac{d^2V}{dx^2} = \frac{1}{3}\pi[(R+x)(-2)+(R-2x).1]

= \frac{1}{3}\pi[-2R-2x+R-2x]

= \frac{1}{3}\pi[-R-4x]

At x = R/3

\frac{d^V}{dx^2}=\frac{1}{3}\pi[-R-4\times \frac{R}{3}]

= \frac{1}{3}[-7R/3]<0

Hence volume of cone is max when x=R/3

Now From eq (i)

V = \frac{1}{3}\pi(R^2-\frac{R^2}{9})(R+\frac{R}{3})

= \frac{1}{3}\pi \frac{8R^2}{9}.\frac{4R}{3}

= \frac{8}{27}.\frac{4}{3}\pi R^3

Volume of cone = \frac{8}{27}\times volume of sphere

A wire of length 28 m is to be cut into two pieces

Leave a Comment