EXERCISE 4.4 (Determinants)
Write Minors and Cofactors of the elements of following determinants:(Class 12 ncert solution math exercise 4.4)
Question 1: (i) ![]()
(ii) ![]()
Solution: (i) The given determinant is ![]()
Minor of element ![]() is
is ![]()
![]() minor of element
minor of element ![]()
![]() minor of element
minor of element ![]()
![]() minor of element
minor of element ![]()
![]() minor of element
minor of element ![]()
Cofactor of ![]() is
is ![]()
![]()
![]()
![]()
![]()
(ii) The given determinant is ![]()
Minor of element ![]() is
is ![]() .
.
![]() minor of element
minor of element ![]()
![]() minor of element
minor of element ![]()
![]() minor of element
minor of element ![]()
![]() minor of element
minor of element ![]()
Cofactor of ![]() is
is ![]()
![]()
![]()
![]()
![]()
Question 2: (i) 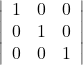
(ii) 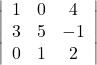
Solution: (i) The given determinant is 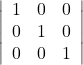
Minor of element ![]() is
is ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cofactor of ![]() is
is ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(ii) The given determinant is 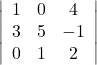
Minor of element ![]() is
is ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cofactor of ![]() is
is ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 3: Using Cofactors of elements of second row, evaluate
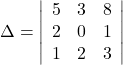
Solution: The given determinant is 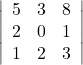
![]() minor of element
minor of element ![]()
![]()
![]()
![]()
![]()
![]()
We know that ![]() is equal to the sum of the product of the elements of the second row with their corresponding cofactors.
is equal to the sum of the product of the elements of the second row with their corresponding cofactors.
Therefore,
![]()
![]()
![]()
![]()
Question 4: Using Cofactors of elements of second row, evaluate
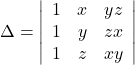
Solution: The given determinant is 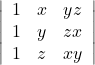
Therefore,
![]()
![]()
![]()
![]()
![]()
![]()
We know that ![]() is equal to the sum of the product of the elements of the third column with their corresponding cofactors.
is equal to the sum of the product of the elements of the third column with their corresponding cofactors.
Therefore,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence,
![]()
Question 5: If  and
and ![]() is Cofactors of
is Cofactors of ![]() , then value of Δ is given by
, then value of Δ is given by
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Solution: We know that ![]() is equal to the sum of the product of the elements of a column or row with their corresponding cofactors.
is equal to the sum of the product of the elements of a column or row with their corresponding cofactors.
![]()
Thus, the correct option is D.