Exercise 7.4(Integration)
Integrate the functions in Exercises 1 to 23.(Ex 7.4 integration ncert maths solution class 12)
Question 1: ![]()
Solution: Let ![]()
![]()
Let ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 2: ![]()
Solution: Let ![]()
![]()
Let ![]()
![]()
![]()
![]()
Using formula :
![]()
Hence, ![]()
![]()
Question 3: ![]()
Solution: Let ![]()
Let ![]()
![]()
![]()
![]()
Using formula :
![]()
Hence,
![]()
![]()
![]()
![]()
![]()
Question 4: ![]()
Solution: Let ![]()
Let ![]() ,
,
![]()
![]()
Now,
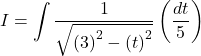
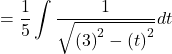
![]()
![]()
Question 5:- ![]()
Solution: let ![]()
Let ![]() ,
,
![]()
![]()
Now,
![]()
![]()
![]()
![]()
![]()
Question 6: ![]()
Solution: Let ![]()
Let ![]()
![]()
![]()
Now,
![]()
![]()
![]()
![]()
Question 7: ![]()
Solution: Let ![]()
![]()
Let ![]() ,
,
Now differentiate both sides,
![]()
![]()
![]()
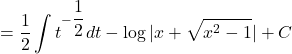
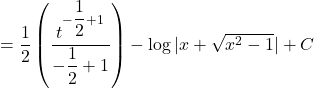
![]()
![]()
![]()
Question 8: ![]()
Solution: Let ![]()
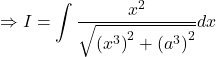
Let ![]() ,
,
![]()
![]()
Now,
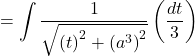
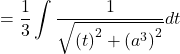
![]()
![]()
Question 9: ![]() .
.
Solution: Let ![]() .
.
Let ![]() ,
,
![]()
![]()
Now,
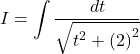
![]()
![]()
Question 10: ![]() .
.
Solution : Let ![]()
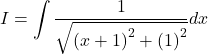
Let x + 1 = t,
Now, differentiate both sides,
dx = dt
Now,
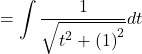
![]()
![]()
![]()
Question 11: ![]() .
.
Solution : Let ![]()
![]()
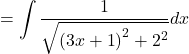
Let ![]()
![]()
![]()
Now,
![]()
![]()
![]()
![]()
![]()
Question 12: ![]() .
.
Solution: Let ![]()
![]()
![]()
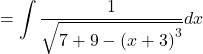
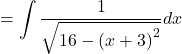
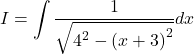
Let, ![]()
![]()
Now,
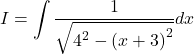
![]()
![]()
![]()
Question 13: ![]() .
.
Solution: Let ![]() .
.
![]()
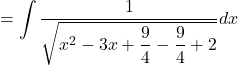
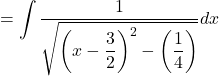
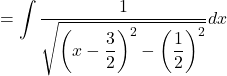
Now, let
![]()
![]()
Now,
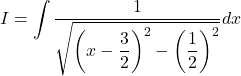
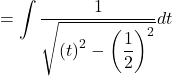
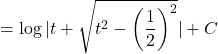
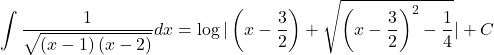
![]()
Question 14: ![]() .
.
Solution: Let ![]() .
.
![]()
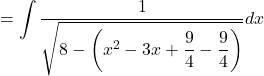
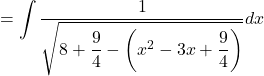
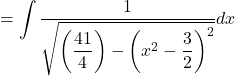
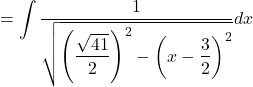
Let ![]()
![]()
Now,
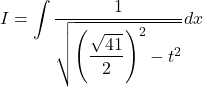
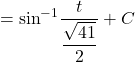
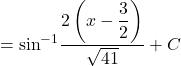
![]()
Question 15: ![]() .
.
Solution: Let ![]()
![]()
![]()
![]()
hence,
![Rendered by QuickLaTeX.com \displaystyle \int {\dfrac{1}{{\sqrt {\left( {x - a} \right)\left( {x - b} \right)} }}dx} = \displaystyle \int {\dfrac{1}{{\sqrt {{{\left[ {x - \left( {\dfrac{{a + b}}{2}} \right)} \right]}^2} - {{\left( {\dfrac{{a - b}}{2}} \right)}^2}} }}dx}](https://gmath.in/wp-content/ql-cache/quicklatex.com-fe80c7fba9d5a482b5fdfdfb0b753f75_l3.png)
Now, let
![]()
![]()
Now,
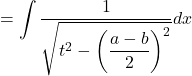
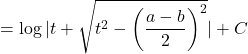
![]()
Question 16: ![]() .
.
Solution: Let ![]()
Let ![]()
![]()
Now,
![]()
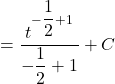
![]()
![]()
Question 17: ![]() .
.
Solution: Let ![]()
![]()
![]()
let ![]()
![]()
![]()
![]()
![]()
![]()
Question 18:![]() .
.
Solution: Let ![]() .
.
![]()
![]()
![]()
![]()
![]()
Let ![]() ,
,
![]()
![]()
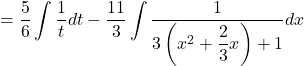
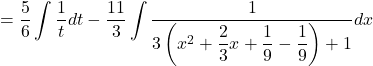
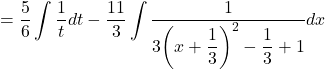
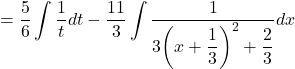
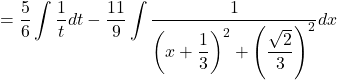
![]()
![]()
Question 19: ![]() .
.
Solution: Let ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Let ![]() ,
,
![]()
![]()
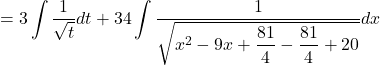
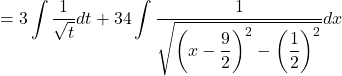
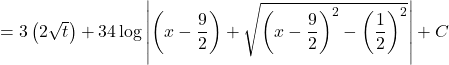
![]()
Question 20: ![]() .
.
Solution: Let ![]() .
.
![]()
![]()
![]()
![]()
![]()
Let ![]() ,
,
![]()
![]()
![]()
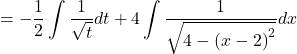
![]()
![]()
Question 21:![]() .
.
Solution: Let ![]()
![]()
![]()
![]()
![]()
![]()
Let ![]() ,
,
![]()
![]()
![]()
![]()
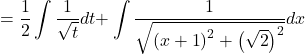
![]()
![]()
Question 22: ![]() .
.
Solution: Let ![]()
![]()
![]()
![]()
![]()
Let ![]() ,
,
![]()
![]()
![]()
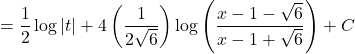
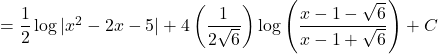
Question 23:![]() .
.
Solution: Let ![]()
![]()
![]()
![]()
![]()
Let ![]() ,
,
![]()
![]()
![]()
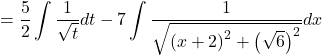
![]()
![]()
Choose the correct answer in Exercises 24 and 25.
Question 24: ![]() is equals to:
is equals to:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Solution: the correct answer is B.
Let ![]()
![]()
![]()
![]()
![]()
Thus, the correct answer is B.
Question 25: ![]() is equals to:
is equals to:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Solution: the correct answer is B.
Let ![]()
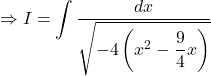
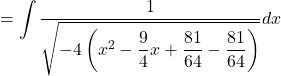
![Rendered by QuickLaTeX.com = \displaystyle \int {\dfrac{1}{{\sqrt { - 4\left[ {{{\left( {x - \dfrac{9}{8}} \right)}^2} - {{\left( {\dfrac{9}{8}} \right)}^2}} \right]} }}dx}](https://gmath.in/wp-content/ql-cache/quicklatex.com-1fc6d3ecbba82f96d2bfa87de943d0ff_l3.png)
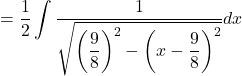
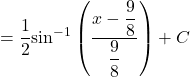
![]()
Thus, the correct answer is B.
