EXERCISE 5.6
If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find![]() .(Class 12 ncert solution math exercise 5.6)
.(Class 12 ncert solution math exercise 5.6)
Question 1: ![]() ,
,
Solution: Given, ![]()
Then,
![]()
![]()
![]()
![]()
![]()
![]()
Question 2: ![]()
Solution: Given, ![]()
Then,
![]()
![]()
![]()
![]()
![]()
![]()
Question 3: ![]()
Solution: Given, ![]()
Then, ![]()
![]()
![]()
![]()
![]()
![]()
Question 4: ![]()
Solution: Given, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 5: ![]()
Solution: Given, ![]()
Then,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 6: ![]()
Solution: Given, ![]()
Then,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 7: ![]()
Solution: Given, ![]()
Then,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 8: ![]()
Solution: ![]()
Then,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore,
![]()
![]()
![]()
Question 9: ![]()
Solution: Given, ![]()
Then,
![]()
![]()
Therefore,
![]()
![]()
![]()
![]()
![]()
![]()
Question 10: ![]()
Solution: Given, ![]()
Then,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore,
![]()
![]()
![]()
Question 11: If ![]() , show that
, show that ![]()
Solution: Given, ![]() and
and ![]()
Hence,
![]()
![]()
![]()
![]()
![]()
![]()
Consider ![]()
Taking log on both sides, we get
![]()
Therefore,
![]()
![]()
![]()
Now, ![]()
Taking log on both sides, we get
![]()
Therefore,
![]()
![]()
![]()
Hence,
![]()
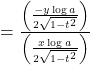
![]()

