EXERCISE 4.6 ( Determinants )
Question 1: Examine the consistency of the system of equations:(Class 12 ncert solution math exercise 4.6)
![]()
Solution: ![]()
The given system of equations is: ![]()
The given system of equations can be written in the form of ![]() , where
, where
![]()
Hence,
![]()
=3-4
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
Thus, the given system of equations is consistent.
Question 2: Examine the consistency of the system of equations:
![]()
![]()
Solution: ![]()
The given system of equations is: ![]()
The given system of equations can be written in the form of ![]() , where
, where
![]()
Hence,
![]()
=2+1
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
Hence, the given system of equations is consistent.
Question 3: Examine the consistency of the system of equations:
![]()
![]()
Solution: ![]()
The given system of equations is: ![]()
The given system of equations can be written in the form of ![]() , where
, where
![]()
Hence,
![]()
=6-6
=0
So, ![]() is a singular matrix.
is a singular matrix.
Now,
![]()
Therefore,
![]()
![]()
![]()
Thus, the solution of the given system of equations does not exist.
Hence, the system of equations is inconsistent.
Question 4: Examine the consistency of the system of equations:
![]()
![]()
![]()
Solution: ![]()
![]()
The given system of equations is: ![]()
The given system of equations can be written in the form of ![]() , where
, where
![Rendered by QuickLaTeX.com A=\begin{bmatrix} 1 & 1 & 1 \\ 2 & 3 & 2 \\ a & a & 2 a \end{bmatrix}, X=\left[\begin{array}{l} x \\ y \\ z \end{array}\right] \text { and } \quad B=\left[\begin{array}{l} 1 \\ 2 \\ 4 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-678a55660a492c94eeb4c2f24d7687c5_l3.png)
Hence,
![]()
![]()
![]()
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
Thus, the given system of equations is consistent.
Question 5:Examine the consistency of the system of equations:
![]()
![]()
![]()
Solution:The given system of equations is:
![]()
![]()
![]()
The given system of equations can be written in the form of ![]() , where
, where
![Rendered by QuickLaTeX.com A=\begin{bmatrix} 3 & -1 & -2 \\ 0 & 2 & -1 \\ 3 & -5 & 0 \end{bmatrix}, X=\left[\begin{array}{l} x \\ y \\ z \end{array}\right] \text { and } B=\left[\begin{array}{c} 2 \\ -1 \\ 3 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-d2599aae8f630ce072651c4751a53f36_l3.png)
Hence,
![]()
![]()
![]()
So, ![]() is a singular matrix.
is a singular matrix.
Now,
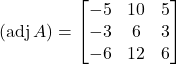
Therefore,
![Rendered by QuickLaTeX.com (\text { adji }) B =\begin{bmatrix} -5 & 10 & 5 \\ -3 & 6 & 3 \\ -6 & 12 & 6 \end{bmatrix}\left[\begin{array}{c} 2 \\ -1 \\ 3 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-f20ac5c72a174acaf22afe4550d919d5_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow \left[\begin{array}{c} -10-10+15 \\ -6-6+9 \\ -12-12+18 \end{array}\right] \\ =\left[\begin{array}{l} -5 \\ -3 \\ -6 \end{array}\right] \\ \neq 0](https://gmath.in/wp-content/ql-cache/quicklatex.com-f00d5aa99875bd68c385f4178e2153c6_l3.png)
Thus, the solution of the given system of equations does not exist.
Hence, the system of equations is inconsistent.
Question 6:Examine the consistency of the system of equations:
![]()
![]()
![]()
Solution:The given system of equations is:
![]()
![]()
![]()
The given system of equations can be written in the form of ![]() , where
, where
![Rendered by QuickLaTeX.com A=\begin{bmatrix} 5 & -1 & 4 \\ 2 & 3 & 5 \\ 5 & -2 & 6 \end{bmatrix}, X=\left[\begin{array}{l} x \\ y \\ z \end{array}\right] \text { and } B=\left[\begin{array}{c} 5 \\ 2 \\ -1 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-69ef08f34ee3fbb85d40cc024c9f7c6c_l3.png)
Hence,
![]()
![]()
![]()
![]()
So, ![]() is nonsingular. Therefore,
is nonsingular. Therefore, ![]() exists.
exists.
Hence, the given system of equations is consistent.
Question 7: Solve system of linear equations, using matrix method.
![]()
![]()
Solution: ![]()
The given system of equations is: ![]()
The given system of equations can be written in the form of ![]() , where
, where
![]()
Hence,
![]()
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
Now,
![]()
![]()
Then,
![]()
![Rendered by QuickLaTeX.com \Rightarrow\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{cc} 3 & -2 \\ -7 & 5 \end{array}\right]\left[\begin{array}{l} 4 \\ 5 \end{array}\right] \\ \Rightarrow\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{c} 12-10 \\ -28+25 \end{array}\right] \\ \Rightarrow\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{c} 2 \\ -3 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-8afa5e106caea0d143d56b71e1c1c739_l3.png)
Hence, ![]() and
and ![]()
Question 8: Solve system of linear equations, using matrix method.
![]()
![]()
Solution: ![]()
The given system of equations is: ![]()
The given system of equations can be written in the form of
![]() ,
,
where ![]() and
and ![]()
Hence,
![]()
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
Now,
![]()
![]()
Therefore,
![]()
![]()
![]()
![]()
![]()
Hence, ![]() and
and ![]()
Question 9: Solve system of linear equations, using matrix method.
![]()
![]()
Solution:![]()
The given system of equations is: ![]()
The given system of equations can be written in the form of ![]() , where
, where
![]()
Hence,
![]()
![]()
So, ![]() is nonsingular. Therefore,
is nonsingular. Therefore, ![]() exists.
exists.
Now,
![]()
![]()
Therefore,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence, ![]() and
and ![]()
Question 10: Solve system of linear equations, using matrix method.
![]()
![]()
Solution: ![]()
The given system of equations is: ![]()
The given system of equations can be written in the form of ![]() , where
, where
![]()
Hence,
![]()
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
Now,
![]()
![]()
Therefore,
![]()
![]()
![]()
![]()
![]()
![]()
Hence, ![]() and
and ![]()
Question 11: Solve system of linear equations, using matrix method.
![]()
![]()
![]()
Solution:The given system of equations is:
![]()
![]()
![]()
The given system of equations can be written in the form of ![]() , where
, where
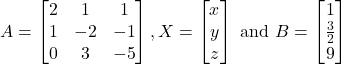
Hence,
![]()
![]()
![]()
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
![]()
![]()
![]()
Hence,
Therefore,
![]()
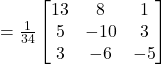
![]()
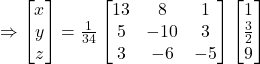
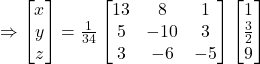
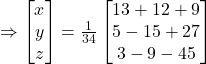

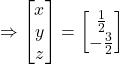
Hence, ![]() and
and ![]()
Question 12: Solve system of linear equations, using matrix method.
![]()
![]()
![]()
Solution:The given system of equations is:
![]()
![]()
![]()
The given system of equations can be written in the form of ![]() , where
, where
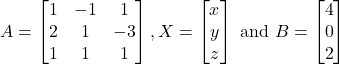
Hence,
![]()
![]()
![]()
So, ![]() is nonsingular.
is nonsingular.
Therefore, ![]() exists.
exists.
Now,
![]()
![]()
![]()
Hence,
![]()
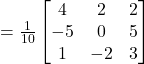
Therefore,
![]()
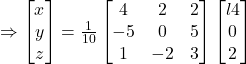
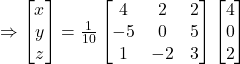

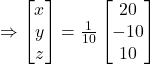
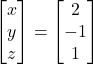
Hence, ![]() and
and ![]()
Question 13: Solve system of linear equations, using matrix method.
![]()
![]()
![]()
Solution:The given system of equations is:
![]()
![]()
![]()
The given system of equations can be written in the form of ![]() , where
, where
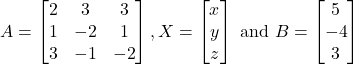
Hence,
![]()
![]()
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
Now,
![]()
![]()
![]()
Hence,
![]()

Therefore,
![]()
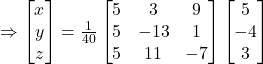
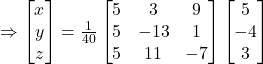
 .
.
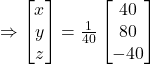
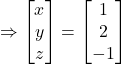
Hence, ![]() and
and ![]()
Question 14:Solve system of linear equations, using matrix method.
![]()
![]()
![]()
Solution:The given system of equations is:
![]()
![]()
![]()
The given system of equations can be written in the form of ![]() , where
, where
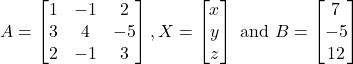
Hence,
![]()
![]()
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists
exists
![]()
![]()
![]()
Hence,
![]()
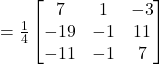
Therefore,
![]()
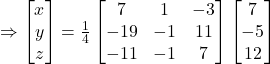
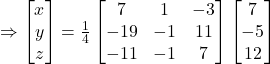


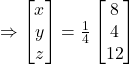
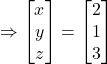
Hence, ![]() and
and ![]()
Question 15: 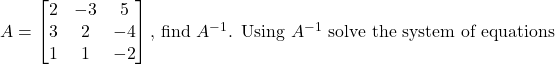
![]()
![]()
![]()
Solution: It is given that 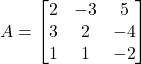
Therefore,
![]()
![]()
![]()
Now,
![]()
![]()
![]()
Hence,
![]()
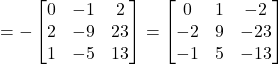
The given system of equations can be written in the form of ![]() , where
, where

The solution of the system of equations is given by ![]() .
.
Therefore,
![]()
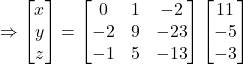
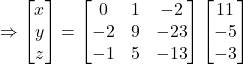
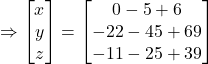
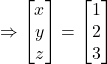
Hence, ![]() and
and ![]()
Question 16: The cost of 4 kg onion, 3 kg wheat and 2 kg rice is ₹ 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is ₹ 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is ₹ 70 . Find cost of each item per kg by matrix method.
Solution: Let the cost of onions, wheat, and rice per ![]() in
in ![]() be
be ![]() and
and ![]() respectively.
respectively.
Then, the given situation can be represented by a system of equations as:
![]()
![]()
![]()
The given system of equations can be written in the form of ![]() , where
, where
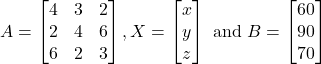
Therefore,
![]()
![]()
![]()
So, ![]() is non-singular.
is non-singular.
Therefore, ![]() exists.
exists.
Now,
![]()
![]()
![]()
Therefore,
![]()
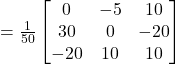
Hence,
![]()
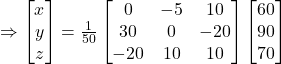
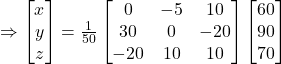
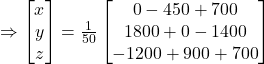
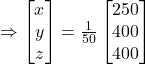
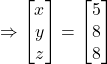
Thus, ![]() and
and ![]()
Hence, the cost of onions is ₹ 5 per kg the cost of wheat is ₹ 8 per kg, and the cost of rice is ₹ 8 per kg.