Class 10 Case based problem of Chapter 3 Pair of Linear eq 2

by

Chapter 3:Pair of Linear equation in two variables

Class 10 Case based problem of Chapter 3 Pair of Linear eq 1

Class 10 Case based problem of Chapter 3 Pair of Linear eq 2

Case Based :3

  Mr. Jose decided to go to an amusement park along with his family. The cost of a entry ticket is ₹ 2500 for Children and ₹ 5000 for adults. On that particular day. attendence at the circus is 2,000 and the total gate revenue is ₹ 70,00,000.(Class 10 Case based problem of Chapter 3 Pair of Linear eq 2)

Class 10 Case based problem of Chapter 3 Pair of Linear eq 2

(A) If we let the number of children and adults who bought ticket on that day as x and y respectively, form the pair of linear equations describing the above situation. Hence, find the number of children and adults who bought tickets on that particular day.

(B) Find the points where the lines represented by the equations 2x – 3y + 4 = 0 and x + 2y – 5 = 0 respectively intersect the x-axis.

Solution:

(A) the number of children who bought ticket = x

the number of adults who bought ticket = y

First condition:

 x + y = 2,000 ……..(i)

Second condition

2,500 x + 5,000 y = 70,00,000

Divide by 2,500

x + 2y = 2800 ….(ii)

Subtracting (i) to (ii)

(x + y) – (x + 2y) = 2000 -2800

⇒ x + y – x – 2y = – 800

⇒ – y = -800

⇒ y = 800

Replacing on equation (i)

x + y = 2000

⇒ x + 800 = 2000

⇒ x = 2000 – 800

⇒ x = 1200

the number of children who bought ticket = 1200

the number of adults who bought ticket = 800

(B) On x-axis y = 0

So, substituting y = 0 in the equations 2x – 3y + 4 = 0 and x + 2y -5 = 0, we get

2x – 3×0 + 4 =0

⇒ 2x = -4

⇒ x = -2

(-2, 0)

And,  x + 2×0 – 5 = 0

⇒ x = 5

(5, 0)

Hence, the equations will intersect the x- axis at points (-2, 0) and (5, 0) Respectively

Case Based :4

A test consists of ‘True’ or ‘False’ questions. One marks is awarded for every correct answer while 1/4 mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing. He answered 120 questions and got 90 marks.

(A) If answer to all questions he attempted by guessing were wrong, then how many questions did he answer correctly ?

(B) If answer to all questions be attempted by guessing were wrong then how many questions he answered correctly to score 95 marks ?

Solution:

(A) Let the number of questions he answered correctly = x

Let the number of questions he answered by guessing = y

First condition

x + y = 120 ……..(i)

Second condition

x + y\times (-\frac{1}{4}) = 90

⇒ 4x – y = 360 ……(ii)

Adding (i) and (ii)

(x + y) + (4x -y) = 120 + 360

⇒ x + y + 4x – y = 480

⇒  5x = 480

⇒ x = 96

Replacing in eq (i)

x + y = 120

⇒ 96 + y = 120

⇒ y = 120 – 96

⇒ y = 24

Hence, he answered 96 question correctly.

(B) Let number of question he answered correctly = x

Number of question he answered by guessing = 120 – x

So, x×1 + (120 – x)×(-1/4) = 95

\Rightarrow 4x - (120 - x) = 380

\Rightarrow 5x = 380 + 120

\Rightarrow 5x = 500

\Rightarrow x = 100

Hence, he answered  100 questions correctly 

Case Based : 5

Amrita was very fond of reading books. So, she went to the national book fair at Pragati Maidan in New Delhi to get some story books and text books.

When her friends asked her how many of each she had bought, she answered, four times the number of text books is six more than thrice the number of story books. Also, seven times the number of text books added to thrice the number of story books gives 27.

Class 10 Case based problem of Chapter 3 Pair of Linear eq 2

(A) Taking the number of text books and story books bought by Amrita as x and y respectivly, the pair of linea equations formed in this case is:

(a) 4x + 3y = 6; 7x + 3y = 27

(b) 4x – 3y = -6; 7x + 3y = 27

(c) 4x – 3y = 6; 7x + 3y = 27

(d) 4x – 3y = -6; 7x – 3y = 27

(B) The number of text books and story books bought by Amrita from the fair are :

(a) Text books = 4, Story books = 3

(b) Text books = 4, Story books = 6

(c) Text books = 6, Story books = 4

(d) Text books = 3, Story books = 2

(C) The area of the triangle form by the graphs of the two equations obtained and the y-axis is:

(a) 9 sq. units             (b) 11 sq. units

(c) 16.5 sq.units         (d) 18 sq. units

(D) The value of k for which the system of equations kx + 3y = k -3; 12x + ky = k has no solution is:

(a) k = 6                       (b) k = -6

(c) k = 6 and k = -6    (d) k = 1

(E) The linear equation 2x – y = 4 intersects the y-axis at the point:

(a) (0, -4)                      (b) (2, -8)

(c) (0, 4)                         (d) (4, 0)

Solution:

(A) Answer (c) 4x – 3y = 6; 7x + 3y = 27

Explanation:

Let Amrita bought text books = x

And Story books = y

First condition

4x = 3y + 6

⇒ 4x – 3y = 6 ………(i)

Second condition

7x + 3y = 27 ………(ii)

(B) Answer (d) Text books = 3, Story books = 2

Explanation:

Adding eq (i) and (ii)

(4x – 3y) + (7x + 3y) = 6 + 27

⇒ 4x – 3y + 7x + 3y = 33

⇒ 11x  = 33

⇒ x = 3

Replacing in eq (i)

4x – 3y = 6

⇒ 4×3 – 3y = 6

⇒ -3y = 6 – 12

⇒ -3y = -6

⇒ y = 2

Therefore, number of text books = 3,

Number of Story books = 2

(C) Answer (c) 16.5 sq. units

From graph

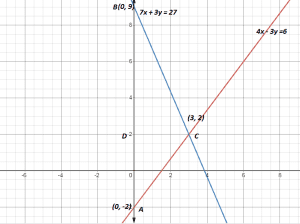
7x + 3y = 27;4x - 3y = 6

Area of triangle = \frac{1}{2} \times AB \times DC

= \frac{1}{2} \times 11 \times 3

= 16.5 sq. units

(D) Answer (b) k = -6

Explanation: For no solution,

\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}\neq\dfrac{c_1}{c_2}

\dfrac{k}{12}=\dfrac{3}{k}\neq \dfrac{k-3}{k}

Simplifying the equation, \dfrac{k}{12}=\dfrac{3}{k}

\Rightarrow k^2 = 36

\Rightarrow k = \pm 6

Again taking

\dfrac{3}{k}\neq\dfrac{k-3}{k}

\Rightarrow k - 3 = 3

\Rightarrow k = 6 it does not satisfy the given equation.

Therefore, k = -6 is the correct answer.

(E) Answer (a) (0, -4)

Explanation: For point on y-axis x = 0 putting in 2x – y = 4

\Rightarrow 2\times 0- y = 4

\Rightarrow y = -4

Hence, point on y-axis = (0, -4)

 

Class 10 Case based problem of Chapter 3 Pair of Linear eq 1
Raman went to a local mela during dussehra.

Class 10 Case based problem of Chapter 2 Polynomials 1

Class 10 Case based problem of Chapter 2 Polynomials 2

Class 10 Case based problem of Chapter 2 Polynomials 3

Gmath.in

Leave a Comment