“Boost your class 12 revision of cbse math part-I 2022-2023 Math preparation with our comprehensive Revision Part-I guide. Get clear concepts, key formulas, and expert tips to ace your exams. Visit gmath.in now!”
Fast revision(Math)
class 12 revision of cbse math part-I 2022-2023
Class 12 revision of cbse math part-II 2022-2023

Chapter 1: Relation and function
EXERCISE 1.1(Relation)
1. Relation: If A and B are two non empty sets, then any subset R of ![]() is called relation from set A to set B.
is called relation from set A to set B.
i.e. ![]()
For example: Let A = {1,2},B={3,4}
Then A×B = {(1,3),(1,4),(2,3),(2,4)}
A subset ![]() is called relation from A to B.
is called relation from A to B.
Similarly, other subsets of ![]() are also relation from A to B.
are also relation from A to B.
Domain:- Domain of R is the set of all first coordinates of elements of R and it is denoted by Dom(R)
Range:- Range of R is the set of all second coordinates of R and it is denoted by range (R).
NOTE:- A relation R on set A mens, the relation from A to A i.e., $R\subseteq A\times A$
Some standard relation:-
Let A be a non empty set. then, a relation R on set A ,Then
(a) Reflexive : If ![]() for each element
for each element ![]()
(b)Symmetric: If ![]() for all
for all ![]()
(c) Transitive: If ![]() and
and ![]() for all
for all ![]()
Equivalence Relation :- Any relation R on a set A is said to be an equivalence relation if R is reflexive,symmetric and transitive.
Equivalence class: Let R be an equivalence relation on a non-empty set A. For all ![]() , the equivalence class of “a” is defined as the set of all such elements of A which are related to “a” under R. It is denoted by [a].
, the equivalence class of “a” is defined as the set of all such elements of A which are related to “a” under R. It is denoted by [a].
i.e. [a] = equivalence class of ‘a’ ![]()
For example, Let A = {1, 2, 3} and R be the equivalence relation on A given by
R = {(1,1),(2,2),(3,3),(1,2),(2,1)}
The equivalence class are
[1]=equivalence class of 1 = {1,2}
[2] = {1,2} ,[3] ={3}
Hence [1]=[2]
Exercise 1.2
Function:- A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.
In other words, a function f is a relation from a non-empty set A to a non-empty
set B such that the domain of f is A and no two distinct ordered pairs in f have the
same first element.
If f is a function from A to B and ![]() , then f (a) = b, where b is called the image of a under f and a is called the preimage of b under f.
, then f (a) = b, where b is called the image of a under f and a is called the preimage of b under f.
Types of functions:
One-one(Injective):- A function ![]() is defined to be one-one (or injective), if the images
is defined to be one-one (or injective), if the images
of distinct elements of X under f are distinct,
Let ![]()
![]()
![]() .
.
Many-one: – A function ![]() is defined to be many-one , if the images of distinct elements of X under f are Same,
is defined to be many-one , if the images of distinct elements of X under f are Same,
Let ![]()
![]()
![]() .
.
Onto(Surjective):-A function ![]() is said to be onto (or surjective), if every element of Y is the image of some element of X under f, i.e., for every
is said to be onto (or surjective), if every element of Y is the image of some element of X under f, i.e., for every ![]() , there exists an element x in X such that f (x) = y.
, there exists an element x in X such that f (x) = y.
One-one and Onto(Bijective):- A function ![]() is said to be bijective,if f is both one-one and onto.
is said to be bijective,if f is both one-one and onto.
Number of function:
(i) If X and Y two finite sets having m and n elements respectively then the number of functions from X to Y is
![]()
(ii) If ![]() ,
, ![]() then number of one-one functions from A to B =
then number of one-one functions from A to B = 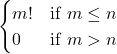
(iii) If ![]() then number of onto functions from A to B
then number of onto functions from A to B 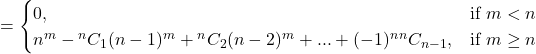
Chapter 2: Inverse trigonometric function
EXERCISE 2.1
1. ![]() should not be confused with
should not be confused with ![]() . In fact
. In fact ![]() and similarly for other trigonometric functions.
and similarly for other trigonometric functions.
2. Whenever no branch of an inverse trigonometric functions is mentioned, we mean the principal value branch of that function.
3. The value of an inverse trigonometric functions which lies in the range of principal branch is called the principal value of that inverse trigonometric functions.
The following table gives the inverse trigonometric function (principal value branches) along with their domains and ranges
![Rendered by QuickLaTeX.com \begin{array}{|c|c|c|} \hline \text { Function } & \text { Domain } & \text { Range } \\ \hline \sin ^{-1}x & {[-1,1]} & {[-\pi / 2, \pi / 2]} \\ \hline \cos ^{-1} x& {[-1,1]} & {[0, \pi]} \\ \hline \tan ^{-1}x & R & {[-\pi / 2, \pi / 2)} \\ \hline \cot ^{-1} x& R & {[0, \pi]} \\ \hline \sec ^{-1}x & \mathbb{R}-(-1,1] & {[0, \pi]-\{\pi / 2\}} \\ \hline \operatorname{cosec}^{-1} x& R-[-1,1) & {[-\pi / 2, \pi / 2]-\{0\}} \\ \hline \end{array}](https://gmath.in/wp-content/ql-cache/quicklatex.com-d31168525177e37e23f7e7a90ca94697_l3.png)
EXERCISE 2.2
Inverse trigonometric formulae
(1) (a) ![]() or
or ![]()
(b) ![]() or
or ![]()
(c) ![]()
(2) (a) ![]()
(b) ![]()
(c) ![]() i
i ![]()
(3) (a) ![]()
(b) ![]() ;
; ![]()
(c) ![]()
(4) (a) ![]()
(b) ![]()
(c) ![]() i
i ![]()
(5) (a) ![]()
(b) ![]()
(6) (a) ![]() i
i ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(d) ![]()
(e) ![]()
(7) (a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
8. Important substitution to simply trigonometrical expression involving inverse trigonometrical functions.
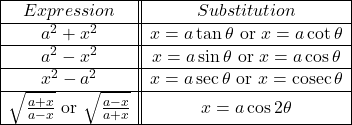
Chapter 3:
Exercise 3.1
Matrix:- A matrix is a recangular arrangement of numbers or functionsarranged into a fixed number of row and column.
Each entry in a amtrix is called an element of the matrix
Order of matrix:- Row × column
Name of elements in 3× 3 matrix
Let 
Row matrix: A matrix having one row is called row matrix.
EX:- ![]()
Column matrix:- A matrix having only one column is called column matrix.
EX:- ![]()
Square matrix: A matrix in which the number of rows is equal to the the no of column, called a square matrix.
Diagonal matrix:- A square matrix ![]() is said to be a diagonal matrix
is said to be a diagonal matrix ![]() for
for ![]() .
.
Ex: 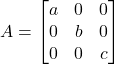
We can write this matrix as ![]()
Scalar matrix:- A square matrix is said to be scalar matrix and entries on its principal diagonal are equal.
(i) ![]() (ii)
(ii) ![]() where
where ![]() .
.
Ex:- 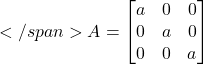
Identity matrix: A sqare matrix in which all non diagonal elements are zero and all diagonal elements are equal to 1 is called identity matrix.
(i) ![]() (ii)
(ii) ![]()
EX:- 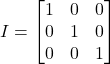
Null matrix or Zero matrix:- A matrix whose elements are zero is called a null matrix or a zero matrix
Ex:- 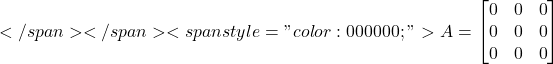
Equality of matrices
Definition : Two matrices ![]() and
and ![]() are said to be equal if
are said to be equal if
(i) they are of the same order
(ii) each element of A is equal to the corresponding element of B, that is ![]() for all i and j..
for all i and j..
For example, ![]() and
and ![]() are equal matrices
are equal matrices
Exercise 3.2
NOTE:- (i)matrix addition follow commutative law
![]()
(ii) Matrix multiplication does not follow commutative law
![]()
(ii) We know that, for real numbers a, b if ab = 0, then either a = 0 or b = 0. This need not be true for matrices,
Matrix multiplication:
![]()
![]()
![]()
Possibility of multiplication of two matrix
Let A and B are two matrices whose orders rae $m\times n$ and $p\times q$
multiplication of two matrices ![]() is possible if
is possible if ![]() . its mean post multiplier of A should be equal to pre multiplier of B.
. its mean post multiplier of A should be equal to pre multiplier of B.
Exercise 3.3
Transpose of a Matrix
Definition :- If ![]() be an m × n matrix, then the matrix obtained by interchanging the rows and columns of A is called the transpose of A. Transpose of the matrix A is
be an m × n matrix, then the matrix obtained by interchanging the rows and columns of A is called the transpose of A. Transpose of the matrix A is
denoted by ![]() or
or ![]() . In other words, if
. In other words, if ![]() , then
, then ![]() .
.
For example: ![]()
Then 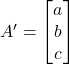
Properties of transpose of the matrices
For any matrices A and B of suitable orders, we have
(i) ![]() , (ii)
, (ii) ![]() (where k is any constant)
(where k is any constant)
(iii) ![]() (iv)
(iv) ![]()
(iv) ![]()
Symmetric and Skew Symmetric Matrices
Symmetric Matrices:- A square matrix ![]() is said to be symmetric if
is said to be symmetric if ![]() , that is,
, that is, ![]() for all possible values of i and j.
for all possible values of i and j.
Skew Symmetric Matrices:- A square matrix ![]() is said to be skew symmetric matrix if
is said to be skew symmetric matrix if ![]() , that is
, that is ![]() for all possible values of i and j.
for all possible values of i and j.
Some special points:-
(i) All main diagonal elements of a skew- symmetric matrix are zero.
(ii) Every square matrix can be uniquely expressed as the sum of a symmetric and skew symmetric matrix.
(iii) All positive integral powers of a symmetric matrix are symmetric matrix.
(iv) All odd positive integral powers of a skew-symmetric matrix are skew symmetric matrix.
(v) Any square matrix can be expressed as the sum of a symmetric and a skew symmetric matrix.
![]()
![]() is symmetric matrix
is symmetric matrix
![]() is skew symmetric matrix
is skew symmetric matrix
(vi) If A and B are two square matrices such that ![]() , then B is the inverse matrix of A and is denoted by
, then B is the inverse matrix of A and is denoted by ![]() and A is the inverse of B.
and A is the inverse of B.
(vii) Inverse of a square matrix, if it exists, is unique.
Chapter 4: Determinants
Exercise 4.1
Determinant: Every square matrix can be associated to an expression or a number which is known as its determinant.
If ![]() , then determinant of A is written as
, then determinant of A is written as ![]()
Remarks: (i) For matrix A, |A| is read as determinant of A and not modulus of A.
(ii) Only square matrices have determinants.
Determinants of order two:- ![]()
![]()
Determinants of order three:- 
![]()
(i) There are six ways of expanding a determinant of order
3 corresponding to each of three rows ![]() and three columns
and three columns ![]() giving the same value.
giving the same value.
(ii) In general, if ![]() where A and B are square matrices of order n, then
where A and B are square matrices of order n, then ![]() , where
, where ![]()
Some property of determinants:
(i) The value of the determinant remains unchanged if its rows and columns are interchanged.
(ii) If any two rows (or columns) of a determinant are identical (all corresponding elements are same), then value of determinant is zero.
(iii) If all the elements of any row or any coloumn are zero then the value of determinant of the will be zero.
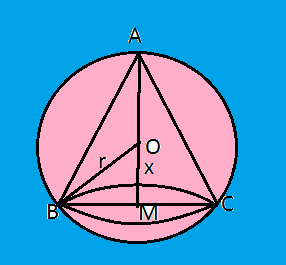
Area of a Triangle: – In earlier classes, we have studied that the area of a triangle whose vertices are ![]() , is given by the expression
, is given by the expression ![]()
Now this expression can be written in the form of a determinant as
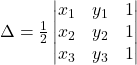
Remarks
(i) Since area is a positive quantity, we always take the absolute value of the determinant
(ii) If area is given, use both positive and negative values of the determinant for calculation.
(iii) The area of the triangle formed by three collinear points is zero.
(iv) If A is a skew symmetric matrix of odd order, then ![]()
(v) The determinant of a skew symmetric matrix of even order is a perfect square.
Minors factor:- Minor of an element ![]() of a determinant is the determinant obtained by deleting its
of a determinant is the determinant obtained by deleting its ![]() row and
row and ![]() column in which element
column in which element ![]() lies. Minor of an element
lies. Minor of an element ![]() is denoted by Mij.
is denoted by Mij.
Remark: Minor of an element of a determinant of order ![]() is a determinant of order
is a determinant of order ![]()
Cofactor:- Cofactor of an element ![]() , denoted by
, denoted by ![]() is defined by
is defined by ![]() , where
, where ![]() is minor of
is minor of ![]() .
.
Let ![]()
![]()
![]()
![]()
![]()
Let 
Then ![]()
Hence ![]() = sum of the product of elements of any row (or column) with their corresponding cofactors.
= sum of the product of elements of any row (or column) with their corresponding cofactors.
![]() If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero. For example,
If elements of a row (or column) are multiplied with cofactors of any other row (or column), then their sum is zero. For example,
![]()
Adjoint of a matrix : The adjoint of a square matrix ![]() is defined as the transpose of the matrix
is defined as the transpose of the matrix ![]() , where Aij is the cofactor of the element
, where Aij is the cofactor of the element ![]() . Adjoint of the matrix A is denoted by
. Adjoint of the matrix A is denoted by ![]() .
.
Let 

Remarks:- If A be any given square matrix of order n, then
![]() , where I is the identity matrix of order n
, where I is the identity matrix of order n
Singular matrix: A square matrix A is said to be singular if ![]() .
.
Some property:
1:- If A and B are nonsingular matrices of the same order, then AB and BA are also nonsingular matrices of the same order.
2:- The determinant of the product of matrices is equal to product of their respective determinants, that is, ![]() , where A and B are square matrices of the same order
, where A and B are square matrices of the same order
3:- If A is a square matrix of order n, then ![]() .
.
4:- A square matrix A is invertible if and only if A is nonsingular matrix.
5:- A is invertible matrix ![]()
6:- ![]()
7:- ![]()
8:- ![]()
9:- ![]()
10:- ![]()
11:- ![]()
12:- ![]()
13:- ![]()
14:- ![]()
15:- Every invertible matrix possesses a unique inverse.
16:- A square matrix is invertble, if it is non singular.
17:- The inverse of an invertible symmetric matrix is a symmetric matrix.
EXERCISE 4.6
Consistent system:- A system of equations is said to be consistent if its solution (one or more) exists.
Inconsistent system:- A system of equations is said to be inconsistent if its solution does not exist.
System of linear equation:-
![]()
![]()
——————–
![]()
![]()
![]()
Case II:– If A is a singular matrix, then ![]() .
.
In this case, we calculate (adj A) B.
If ![]() , (O being zero matrix), then solution does not exist and the
, (O being zero matrix), then solution does not exist and the
system of equations is called inconsistent.
If ![]() , then system may be either consistent or inconsistent according as the system have either infinitely many solutions or no solution.
, then system may be either consistent or inconsistent according as the system have either infinitely many solutions or no solution.
Chapter 5: Differentiation:-
Exercis 5.1
Condition for Continuity:- A function is said to be continuaous at a point a of its domain if
![]()
![]()
![]() Every constant function is continuaous function.
Every constant function is continuaous function.
![]() Every polynomial function is continuous function.
Every polynomial function is continuous function.
![]() Identity function is continuous function.
Identity function is continuous function.
![]() Every logrithmic and exponential function is a continuous function.
Every logrithmic and exponential function is a continuous function.
Some formulae for continuity:-
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
(vi) ![]()
(v) ![]()
Formulae for differentiation
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
(9) ![]()
(10) ![]()
(11) ![]()
(12) ![]()
(13) ![]()
(14) ![]()
(15) ![]()
Product rule
(16) ![]()
Divide rule
(17) 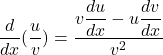
Formulae for Differentiability
![]()
![]()
If ![]() then the function will be differentiable
then the function will be differentiable
Exercise 5.3
Explicit function:When a relationship between x and y is expressed in a way that it is easy to solve for y and write y = f(x), we say that y is given as an explicit function of x.
Example: ![]()
Implicit function: When a relationship between x and y is expressed in a way that it can not solve for y and write y = f(x), we say that y is given as an implicit function of x.
Example: ![]()
Some differentiation formulae for inverse trigonometry function:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
Exercise 5.4 & 5.5
Differentiation of logrithmic function:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
Exercise 5.6
Derivatives of Functions in Parametric Forms
![]()
![]()
Exercise 5.7
Second order derivative
![]()
Chapter 6: Application of derivative
Exercise 6.1
Rate of Change of Quantities:
Rate change with respect to time ![]()
Rate change with respect to x ![]()
![]() is positive if y increases as x increases and
is positive if y increases as x increases and
is negative if y decreases as x increases.
Exercise 6.2:
Increasing and Decreasing Functions
Definition 1:- Let I be an interval contained in the domain of a real valued function f.
Then f is said to be
(i) increasing on I if ![]() in
in ![]()
(ii) decreasing on I, if ![]() in
in ![]() for all
for all ![]()
(iii) constant on I, if $![]() for all x in I, where c is a constant.
for all x in I, where c is a constant.
Theorem 1:- Let f be continuous on $[a, b]$ and differentiable on the open interval ![]() Then
Then
(a) f is increasing in ![]() if
if ![]() for each
for each ![]()
(b) f is decreasing in ![]() if
if ![]() for each
for each ![]()
(c) f is a constant function in ![]() if
if ![]() for each
for each ![]()
Exercise 6.5: Maxima and Minima
First Derivative Test: Let f be a function defined on an open interval I.
Let f be continuous at a critical point c in I. Then
(i) If f’ (x) changes sign from positive to negative as x increases through c, i.e., if f ‘(x) > 0 at every point sufficiently close to and to the left of c, and f ‘(x) < 0 at every point sufficiently close to and to the right of c, then c is a point of local maxima.
(ii) If f ‘(x) changes sign from negative to positive as x increases through c, i.e., if f ‘(x) < 0 at every point sufficiently close to and to the left of c, and f ‘(x) > 0 at every point sufficiently close to and to the right of c, then c is a point of local minima.
(iii) If f ‘(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima. Infact, such a point is called point of inflection
Note:- If c is a point of local maxima of f , then f (c) is a local maximum value of f. Similarly, if c is a point of local minima of f , then f(c) is a local minimum value of f.
Second Derivative Test:- Let f be a function defined on an interval I and ![]() Let f be twice differentiable at c. Then
Let f be twice differentiable at c. Then
(i) x = c is a point of local maxima if ![]() and
and ![]() The value f (c) is local maximum value of f .
The value f (c) is local maximum value of f .
(ii) x = c is a point of local minima if ![]() and
and ![]() In this case, f (c) is local minimum value of f .
In this case, f (c) is local minimum value of f .
(iii) The test fails if ![]() and
and ![]() In this case, we go back to the first derivative test and find whether c is a point of local maxima, local minima or a point of inflexion.
In this case, we go back to the first derivative test and find whether c is a point of local maxima, local minima or a point of inflexion.
Note:- As f is twice differentiable at c, we mean second order derivative of f exists at c.