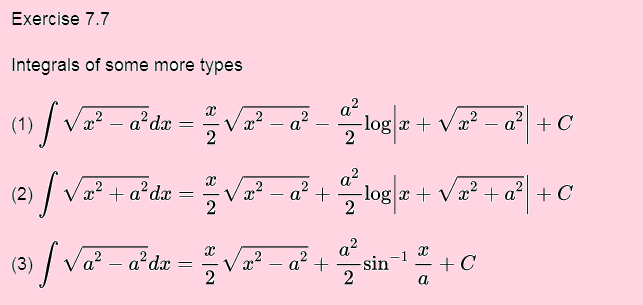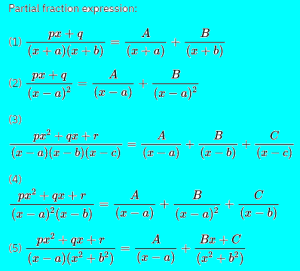Ex 7.7 integration ncert maths solution class 12

Ex 7.7 integration ncert maths solution class 12

by

EXERCISE 7.7(Integration)

Integrate the functions in Exercises 1 to 9.(Ex 7.7 integration ncert maths solution class 12)

Ex 7.7 integration ncert maths solution class 12

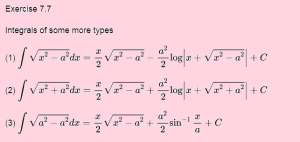
Question 1: \int\sqrt{4-x^2}dx

Solution: Let I=\int \sqrt{4-x^2} d x=\int \sqrt{(2)^2-(x)^2} d x

Since, [\sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+C]

\therefore I=\frac{x}{2} \sqrt{4-x^2}+\frac{4}{2} \sin ^{-1} \frac{x}{2}+C

=\frac{x}{2} \sqrt{4-x^2}+2 \sin ^{-1} \frac{x}{2}+C

Question 2: \int\sqrt{1-4 x^2}dx

Solution: Let, I=\int \sqrt{1-4 x^2} d x=\int \sqrt{(1)^2-(2 x)^2} d x

Put, 2 x=t \Rightarrow 2 d x=d t

\Rightarrow I=\frac{1}{2} \int \sqrt{(1)^2-(t)^2}dt

Since, [\sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+C]

\Rightarrow I=\frac{1}{2}\left[\frac{t}{2} \sqrt{1-t^2}+\frac{1}{2} \sin ^{-1} t\right]+C

=\frac{t}{4} \sqrt{1-t^2}+\frac{1}{4} \sin ^{-1} t+C

=\frac{2 x}{4} \sqrt{1-4 x^2}+\frac{1}{4} \sin ^{-1} 2 x+C

=\frac{x}{2} \sqrt{1-4 x^2}+\frac{1}{4} \sin ^{-1} 2 x+C

Question 3: \int\sqrt{x^2+4 x+6}dx

Solution: Let I=\int \sqrt{x^2+4 x+6} d x

=\int \sqrt{x^2+4 x+4+2} d x

=\int \sqrt{\left(x^2+4 x+4\right)+2} d x

=\int \sqrt{(x+2)^2+(\sqrt{2})^2} d x

Since, \sqrt{x^2+a^2} d x=\frac{x}{2} \sqrt{x^2+a^2}+\frac{a^2}{2} \log \left|x+\sqrt{x^2+a^2}\right|+C

I=\frac{(x+2)}{2} \sqrt{x^2+4 x+6}+\frac{2}{2} \log \left|(x+2)+\sqrt{x^2+4 x+6}\right|+C

=\frac{(x+2)}{2} \sqrt{x^2+4 x+6}+\log \left|(x+2)+\sqrt{x^2+4 x+6}\right|+C

Question 4: \int\sqrt{x^2+4 x+1}dx

Solution: Let, I=\int \sqrt{x^2+4 x+1} d x

=\int \sqrt{\left(x^2+4 x+4\right)-3} d x

=\int \sqrt{(x+2)^2-(\sqrt{3})^2} d x

Since, [\sqrt{x^2-a^2} d x=\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C]

I=\frac{(x+2)}{2} \sqrt{x^2+4 x+1}-\frac{3}{2} \log \left|(x-2)+\sqrt{x^2+4 x+1}\right|+C

Question 5: \int\sqrt{1-4 x-x^2}dx

Solution: Let, I=\int \sqrt{1-4 x-x^2} d x

=\int \sqrt{1-\left(x^2+4 x+4-4\right)} d x

=\int \sqrt{1+4-(x+2)^2} d x

=\int \sqrt{(\sqrt{5})^2-(x+2)^2} d x

Since, [\sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+C]

\Rightarrow I=\frac{(x+2)}{2} \sqrt{1-4 x-x^2}+\frac{5}{2} \sin ^{-1}\left(\frac{x+2}{\sqrt{5}}\right)+C

Question 6: \int\sqrt{x^2+4 x-5}dx

Solution: Let I=\int \sqrt{x^2+4 x-5} d x

=\int \sqrt{\left(x^2+4 x+4\right)-9} d x=\int \sqrt{(x+2)^2-(3)^2} d x

Since, [\int \sqrt{x^2-a^2} d x=\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C]

\Rightarrow I=\frac{(x+2)}{2} \sqrt{x^2+4 x-5}-\frac{9}{2} \log \left|(x+2)+\sqrt{x^2+4 x-5}\right|+C

Question 7: \int \sqrt{1+3 x-x^2}dx

Solution: Put, I=\int \sqrt{1+3 x-x^2} d x

=\int \sqrt{1-\left(x^2-3 x+\frac{9}{4}-\frac{9}{4}\right)} d x

=\int \sqrt{\left(1+\frac{9}{4}\right)-\left(x-\frac{3}{2}\right)^2} d x

=\int \sqrt{\left(\frac{\sqrt{13}}{2}\right)^2-\left(x-\frac{3}{2}\right)^2} d x

Since, [\int \sqrt{a^2-x^2} d x=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \sin ^{-1} \frac{x}{a}+C]

\therefore I=\frac{x-\frac{3}{2}}{2} \sqrt{1+3 x-x^2}+\frac{13}{4 \times 2} \sin ^{-1}\left(\frac{x-\frac{3}{2}}{\frac{\sqrt{13}}{2}}\right)+C

=\frac{2 x-3}{4} \sqrt{1+3 x-x^2}+\frac{13}{8} \sin ^{-1}\left(\frac{2 x-3}{\sqrt{13}}\right)+C

Question 8: \int\sqrt{x^2+3 x}dx

Solution: Let I=\int \sqrt{x^2+3 x} d x

=\int \sqrt{x^2+3 x+\frac{9}{4}-\frac{9}{4}} d x

=\int \sqrt{\left(x+\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2} d x

Since, [\sqrt{x^2-a^2} d x=\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C]

\Rightarrow I=\frac{\left(x+\frac{3}{2}\right)}{2} \sqrt{x^2+3 x}-\frac{\frac{9}{4}}{2} \log \left|\left(x+\frac{3}{2}\right)+\sqrt{x^2+3 x}\right|+C

=\frac{(2 x+3)}{4} \sqrt{x^2+3 x}-\frac{9}{8} \log \left|\left(x+\frac{3}{2}\right)+\sqrt{x^2+3 x}\right|+C

Question 9: \int\sqrt{1+\frac{x^2}{9}}dx

Solution: Let I=\int \sqrt{1+\frac{x^2}{9}} d x

=\frac{1}{3} \int \sqrt{9+x^2} d x

=\frac{1}{3} \int \sqrt{(3)^2+x^2 d x}

Since, [\sqrt{x^2+a^2} d x=\frac{x}{2} \sqrt{x^2+a^2}+\frac{a^2}{2} \log \left|x+\sqrt{x^2+a^2}\right|+C]

\therefore I=\frac{1}{3}\left[\frac{x}{2} \sqrt{x^2+9}+\frac{9}{2} \log \left|x+\sqrt{x^2+9}\right|\right]+C

=\frac{x}{6} \sqrt{x^2+9}+\frac{3}{2} \log \left|x+\sqrt{x^2+9}\right|+C

Question 10: \int \sqrt{1+x^2} is equal to

A. \frac{x}{2} \sqrt{1+x^2}+\frac{1}{2} \log \left|x+\sqrt{1+x^2}\right|+C

B. \frac{2}{3}\left(1+x^2\right)^{\frac{2}{3}}+C

C. \frac{2}{3} x\left(1+x^2\right)^{\frac{2}{3}}+C

D. \frac{x^3}{2} \sqrt{1+x^2}+\frac{1}{2} x^2 \log \left|x+\sqrt{1+x^2}\right|+C

Solution: The correct option is A

Since. [\sqrt{a^2+x^2} d x=\frac{x}{2} \sqrt{a^2+x^2}+\frac{a^2}{2} \log \left|x+\sqrt{x^2+a^2}\right|+C]

\therefore \int \sqrt{1+x^2} d x=\frac{x}{2} \sqrt{1+x^2}+\frac{1}{2} \log \left|x+\sqrt{1+x^2}\right|+C

Thus, the correct option is A.

Question 11: \int \sqrt{x^2-8 x+7} d x is equal to

A. \frac{1}{2}(x-4) \sqrt{x^2-8 x+7}+9 \log \left|x-4+\sqrt{x^2-8 x+7}\right|+C

B. \frac{1}{2}(x+4) \sqrt{x^2-8 x+7}+9 \log \left|x+4+\sqrt{x^2-8 x+7}\right|+C

C. \frac{1}{2}(x-4) \sqrt{x^2-8 x+7}-3 \sqrt{2} \log \left|x-4+\sqrt{x^2-8 x+7}\right|+C

D. \frac{1}{2}(x-4) \sqrt{x^2-8 x+7}-\frac{9}{2} \log \left|x-4+\sqrt{x^2-8 x+7}\right|+C

Solution: The correct option is D

Let I=\int \sqrt{x^2-8 x+7} d x

=\int \sqrt{\left(x^2-8 x+16\right)-9} dx

=\int \sqrt{(x-4)^2-(3)^2} d x

Since, \sqrt{x^2-a^2} d x=\frac{x}{2} \sqrt{x^2-a^2}-\frac{a^2}{2} \log \left|x+\sqrt{x^2-a^2}\right|+C

\therefore I=\frac{(x-4)}{2} \sqrt{x^2-8 x+7}-\frac{9}{2} \log \left|(x-4)+\int \sqrt{x^2-8 x+7}\right|+C

Thus, the correct option is D.

 

Ex 7.6 integration ncert maths solution class 12        Ex 7.5 integration ncert maths solution class 12

Leave a Comment