Case study problem vector 2 chapter 10 class 12

by

Case study Chapter 10( Vector )

Case study 1: A man is watching an aeroplane which is at the co-ordinate point A(4, -1, 3) assuming that the man is at O(0, 0, 0). At the same time he saw a bird at the coordinate point B(2, 0, 4).(Case study problem vector 2)
Based on the above information answer the following:

(a) Find the position vector \vec{AB}

(b) Find the distance between aeroplane and bird

(c) Find the unit vector along \vec{AB} .

(d) Find the direction cosine of \vec{AB} .

(e) Find the angles which \vec{AB} makes with x, y and z axes.

Solution: (a) A(4, -1, 3) and B(2, 0, 4)

Then, \overrightarrow{AB} = (2-4)\hat{i}+(0+1)\hat{j}+(4-3)\hat{k}

= -2\hat{i}+\hat{j}+\hat{k}

(b) Distance between A and B

|\overrightarrow{AB}| = \sqrt{(-2)^2+(1)^2+(1)^2}

=\sqrt{6} units

(c) Unit vector along AB =\frac{\vec{AB}}{|AB|}

= \frac{-2\hat{i}+\hat{j}+\hat{k}}{\sqrt{6}}

= \frac{-2\hat{i}}{\sqrt{6}}+\frac{\hat{j}}{\sqrt{6}}+\frac{k}{\sqrt{6}}

(d) Direction cosine of \vec{AB} are

<\frac{-2}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}}>

(e) Since,
\cos\alpha = \frac{-2}{\sqrt{6}}

\alpha =\cos^{-1}(\frac{-2}{\sqrt{6}})

Again, \cos\beta = \frac{1}{\sqrt{6}}

\beta = \cos^{-1}(\frac{1}{\sqrt{6}})

Again, \cos\gamma = \frac{1}{\sqrt{6}}

\gamma = \cos^{-1}(\frac{1}{\sqrt{6}})

Case study 2:  Ishan left from his village on weekend. First, he travelled up to temple. After this , he left for shoping

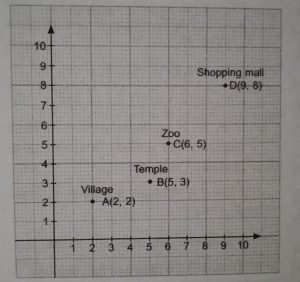
Case study problem vector 2
Ishan left from his village on weekend. First, he travelled up to temple

in a mall. The position of Ishan at different places is given in the following graph.

Based on the above information, answer the following question

(a) Find the position vector of B.

(b) Find the position vector of D.

(c) Represent the vector \vec{BC} in the form of i,j.

(d) Determine the length of vector \vec{AD}.

(e) If \vec{M}= 4\hat{j}+3\hat{k}, then find its unit vector.

Solution: Here (5, 3) are coordinate of B

(a) Since,position vector of B is =\vec{OB}

= 5\hat{i}+3\hat{j}

(b) Here (9, 8) are co-ordinates of D

Then position vector of D = \vec{OD}

= 9\hat{i}+8\hat{j}

(c) \vec{OC} = 6\hat{i}+5\hat{j}

and \vec{OB}= 5\hat{i}+3\hat{j}

vec{BC}=(6\hat{i}+5\hat{j})-(5\hat{i}+3\hat{j})

= 6\hat{i}+5\hat{j}-5\hat{i}-3\hat{j}

= \hat{i}+2\hat{j}

(d) \vec{OD}=9\hat{i}+8\hat{j}

\vec{OA}= 2\hat{i}+2\hat{j}

\vec{AD}= (9\hat{i}+8\hat{j})- (2\hat{i}+2\hat{j})

= 9\hat{i}+8\hat{j}- 2\hat{i}-2\hat{j}

= 7\hat{i}+6\hat{j}

|\vec{AD}|=\sqrt{(7)^2+(6)^2}

\Rightarrow |\vec{AD}|=\sqrt{85} units

(e) We have \vec{M}=4\hat{j}+3\hat{k}

M= \sqrt{(4)^2+(3)^2}

=\sqrt{16+9}=\sqrt{25}

= 5
\hat{M}=\frac{\vec{M}}{|\vec{M}|}

= \frac{4\hat{j}+3\hat{k}}{5}

= \frac{4\hat{j}}{5}+\frac{3\hat{k}}{5}

Case study 3: Employee in a office are following social distance and during lunch they are sitting at places marked by

points A, B and C. Each one is reoresenting position as A(\hat{i}-2\hat{j}+4\hat{k}), B(5\hat{i}+2\hat{k}) and

C(3\hat{i}+2\hat{j}+4\hat{k}).

Based on the above information answer the following:

(a) Find the distance between A and B.

(b) Find the distance between B and C.

(c) Find the position vector \vec{AB}.

(d) Find the unit vector along \vec{AB}.

(e) Find the area enclosed by A, B and C.

Solution: (a) Since, A(\hat{i}-2\hat{j}+4\hat{k}), B(5\hat{i}+2\hat{k})

\vec{AB} = \vec{OB}-\vec{OA}

= (5\hat{i}+2\hat{k})-(\hat{i}-2\hat{j}+4\hat{k})

= 5\hat{i}+2\hat{k}-\hat{i}+2\hat{j}-4\hat{k}

= 4\hat{i}+2\hat{j}-2\hat{k}

|\vec{AB}|= \sqrt{(4)^2+(2)^2+(-2)^2}

= \sqrt{24}=2\sqrt{6}

(b) B(5\hat{i}+2\hat{k}), C(3\hat{i}+2\hat{j}+4\hat{k}).

\vec{BC} = \vec{OC}-\vec{OB}

= (3\hat{i}+2\hat{j}+4\hat{k})-(5\hat{i}+2\hat{k})

= 3\hat{i}+2\hat{j}+4\hat{k}-5\hat{i}-2\hat{k}

= -2\hat{i}+2\hat{j}+2\hat{k}

|\vec{BC}|= \sqrt{(-2)^2+(2)^2+(2)^2}

= \sqrt{12}= 2\sqrt{2}

(c) \vec{AB} = 4\hat{i}+2\hat{j}-2\hat{k}

(d) |\vec{AB}|= 2\sqrt{6}

\hat{AB} = \frac{\vec{AB}}{|\vec{AB}|}

=\frac{4\hat{i}+2\hat{j}-2\hat{k}}{ 2\sqrt{6}}

= \frac{4\hat{i}}{2\sqrt{6}}+\frac{2\hat{j}}{2\sqrt{6}}-\frac{2\hat{k}}{2\sqrt{6}}

= \frac{2\hat{i}}{\sqrt{6}}+\frac{\hat{j}}{\sqrt{6}}-\frac{\hat{k}}{\sqrt{6}}

(e) Since,
\vec{AB} = 4\hat{i}+2\hat{j}-2\hat{k}, \vec{BC} =-2\hat{i}+2\hat{j}+2\hat{k}

Area of triangle ABC = \frac{1}{2}|\vec{AB}\times \vec{BC}|

\vec{AB}\times \vec{BC}=\begin{vmatrix} \hat{i} & \hat{j} &\hat{k} \\ 4 & 2 &-2 \\ -2 & 2 & 2\end{vmatrix}

= \hat{i}(4+4)-\hat{j}(8-4)+\hat{k}(8+4)

= 8\hat{i}-4\hat{j}+12\hat{k}

|\vec{AB}\times \vec{BC}| = \sqrt{(8)^2+(-4)^2+(12)^2}

= \sqrt{64 +16+ 144}

= \sqrt{224}=4\sqrt{14}

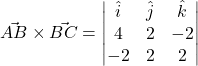
Area =\frac{4\sqrt{14}}{2}

= 2\sqrt{14} sq.units

Some other Case study question:

Solar panels have to be installed carefully so that the tilt of the roof, and the direction to the sun , produce the largest possible electrical power in the solar panals.(Case study problem vector 1)

A surveyor uses his instrument to determine the co-ordinates of the four corners of a roof where solar panels are to

be mounted. In the picture, suppose the points are labelled counter clockwise from the roof corner nearest to the

camera in units of meters P_1(6, 8, 4),P_2(21, 8, 4),P_3(21, 16, 10) and P_4(6, 16, 10).

Based on the above information answer the following question.

Solution: for solution click here

 

Case study three dimension geometry 1
The equation of motion of a missile are x = 3t, y = -4t, z = t where the time
Case study linear programming 1 chapter 12 class 12
Owner of a whole sale computer shop plans to sell two type of computers – a desktop

Leave a Comment