Exercise 8.1(Application of Integrals)
Chapter 8 Exercise 8.1 ncert math solution class 12
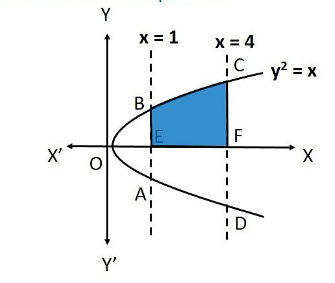
Question1: Find the area of the region bounded by the curve ![]() and the lines
and the lines ![]() and the x-axis.
and the x-axis.
Solution : The area of the region bounded by the curve, ![]() , the lines, x = 1 and x = 4, and the X-axis is the area E B C F.
, the lines, x = 1 and x = 4, and the X-axis is the area E B C F.
Area of ![]()
![]()
![]()
![]()
![]() units
units
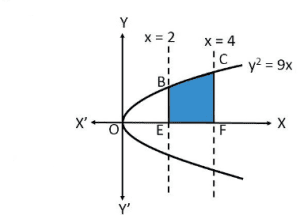
Question 2: Find the area of the region bounded by ![]() and the x – axis in the first quadrant.
and the x – axis in the first quadrant.
Solution : The area of the region bounded by the curve, ![]() , and x = 4, and the x-axis, is the area EBCF.
, and x = 4, and the x-axis, is the area EBCF.
Area of ![]()
![]()
![]()
![]()
![]()
![]() units
units
Question 3: Find the area of the region bounded by ![]() and the y-axis in the first quadrant.
and the y-axis in the first quadrant.
Solution : The area of the region bounded by the curve, ![]() , and y = 4, and the y-axis is the area
, and y = 4, and the y-axis is the area ![]() .
.

Area of ![]()
![]()
![]()
![]()
![]() units
units
Question 4: Find the area of the region bounded by the ellipse ![]()
Solution : The given equation of the ellipse ![]()

It can be observed that the ellipse is symmetrical about x-axis and y-axis.
Area bounded by ellipse ![]() Area of OAB
Area of OAB
Area of ![]()
![]()
![]()
![]()
![]()
![]()
Therefore, area bounded by the ellipse =4 × Area of ![]() units
units
Question 5: Find the area of the region bounded by the ellipse ![]()
Solution : The given equation of the ellipse can be represented as ![]() It can be observed that the ellipse is symmetrical about x-axis and y-axis.
It can be observed that the ellipse is symmetrical about x-axis and y-axis.
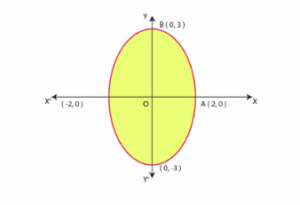
Area bounded by ellipse =4 × Area of OAB
![]()
![]()
![]()
![]()
Therefore, area bounded by the ellipse ![]() Area of
Area of ![]() units
units
Question 6: Find the area of the region in the first quadrant enclosed by x-axis, line ![]() and the
and the ![]()
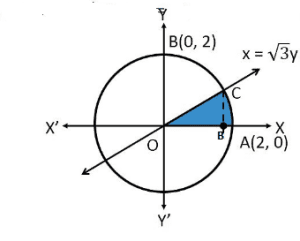
Solution : The area of the region bounded by the circle, ![]() ,line
,line ![]() and the x-axis is the area OAB.
and the x-axis is the area OAB.
Solving ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
and ![]()
The point of intersection of the line and the circle in the first quadrant is ![]() .
.
Area ![]() Area
Area ![]() Area
Area ![]()
Area of ![]()
![]()
![]()
![]()
![]()
![]()
![]() ….(i)
….(i)
![]()
![]()
![]()
![]() …..(ii)
…..(ii)
Adding the equation (1) and (2), we get
The total area of ![]() units
units
Therefore, area enclosed by x – axis, the line ![]() and the circle
and the circle ![]() in the first quadrant is
in the first quadrant is ![]() square units.
square units.
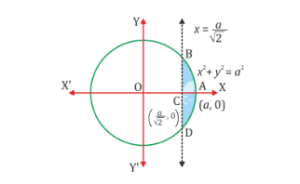
Question 7: Find the area of the smaller part of the circle ![]() cut off by the line
cut off by the line ![]() .
.
Solution : It can be observed that the area ![]() is symmetrical about x -axis.
is symmetrical about x -axis.
Given, ![]()
![]()
Area of ABC ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the area of smaller part of the circle, ![]() , cut off by the line
, cut off by the line ![]() is
is ![]() square units.
square units.
Question 8: The area between ![]() and
and ![]() is divided into two equal parts by the line
is divided into two equal parts by the line ![]() , find the value of a.
, find the value of a.
Solution : The line, x = a, divides the area bounded by the parabola and x = 4 into two equal parts.
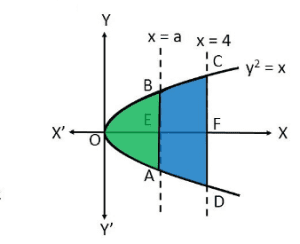
⇒ Area ![]() Area
Area ![]()
It can be observed that the given area is symmetrical about x-axis.
⇒ Area ![]() Area
Area ![]()
Area ![]()
![]()
![]() …..(i)
…..(i)
Area of ![]()
![]()
![]() …..(ii)
…..(ii)
From (1) and (2), we have
![]()
![]()
![]()
![]()
Therefore, the value of a is ![]() .
.
Question 9: Find the area of the region bounded by the parabola ![]() and
and ![]()
Solution: The area bounded by the parabola, ![]() , and the line,
, and the line, ![]() , can be represented as The given area is symmetrical about y-axis.
, can be represented as The given area is symmetrical about y-axis.
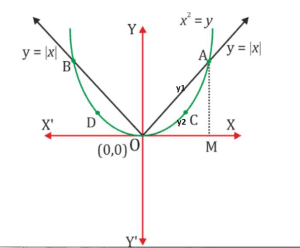
⇒ Area OACO = Area ODBO
Solving ![]() and y = x
and y = x
![]()
![]()
and y = 1 and y = 0
The point of intersection of parabola, ![]() , and line, y = x, is A(1, 1) and (0, 0).
, and line, y = x, is A(1, 1) and (0, 0).
Area of ![]() Area
Area ![]()
Area of ![]()
![]()
![]()
![]()
![]()
Area of ![]()
![]()
![]()
⇒ Area of ![]() Area of
Area of ![]()
![]()
Therefore, required area ![]() units
units
Question 10: Find the area bounded by the curve ![]() and the line
and the line ![]() .
.
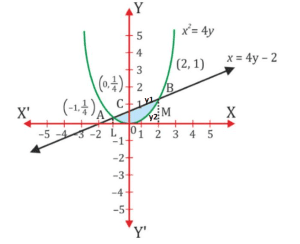
Solution : The area bounded by the curve ![]() and the line
and the line ![]() is represented by the shaded area OBAO.
is represented by the shaded area OBAO.
Solving ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and ![]()
aand y=1 and ![]()
Let A and B be the points of intersection of the line and parabola. Coordinates of point A are ![]() and point B are (2, 1).
and point B are (2, 1).

We draw AL and BM perpendicular to x-axis.
It can be observed that,
Area OBAO ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 11:Find the area of the region bounded by the curve ![]() and the line x=3.
and the line x=3.
Solution : The region bounded by the parabola, ![]() , and the line, x=3, is the area OABO.
, and the line, x=3, is the area OABO.
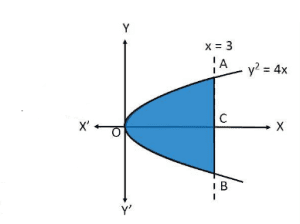
The area OABO is symmetrical about x-axis.
Area of ![]() (Area of
(Area of ![]()
Area ![]()
![]()
![]()
![]()
![]()
Therefore, the required area is ![]() units
units
Question 12: Area lying in the first quadrant and bounded by the circle ![]() and the lines x = 0 and x = 2 is
and the lines x = 0 and x = 2 is
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution : The correct answer is (A).
The area bounded by the circle and the lines, x = 0 and x = 2, in the first quadrant is represented as

Area of ![]()
![]()
![]()
![]() units
units
Thus, the correct answer is (A).
Question 13: Area of the region bounded by the curve ![]() -axis and the line y = 3 is
-axis and the line y = 3 is
(A) 2
(B) ![]()
(C) ![]()
(D) ![]()
Solution : The correct answer is (B)
The area bounded by the curve, ![]() -axis and y = 3 is represented as
-axis and y = 3 is represented as
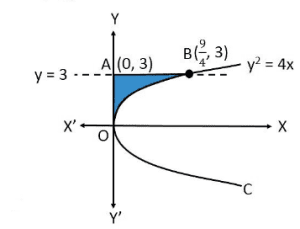
Area ![]()
![]() units
units
Thus, the correct answer is (B).
Chapter 8: Application of Integrals Class 12
Exercise 8.1 ncert math solution class 12