Miscellaneous(Exercise 6)
Question 1: Using differentials; find the approximate value of each of the following.
(a) ![]()
(b) ![]()
Answer : (a) Let ![]()
Let ![]() and
and ![]()
Then, ![]()
![]()
![]()
![]()
Now, dy is approximately equal to ![]() and given by,
and given by,
![]()
![]()
![]()
![]()
Hence, the approximate value of ![]() is
is ![]()
(b) Let ![]()
Let ![]() and
and ![]()
Then, ![]()
![]()
![]()
Now, dy is approximately equal to ![]() and is given by,
and is given by,
![]()
![]()
Hence, the approximate value of ![]() is
is ![]()
Question 2: Show that the function given by ![]() has maximum at
has maximum at ![]() .
.
Answer : The given function is ![]()
![]()
Now,![]()
![]()
![]()
Now, ![]()
![]()
Now, ![]()
![]()
Therefore, by second derivative test, ![]() is the maximum at
is the maximum at ![]() .
.
Question 3: The two equal sides of an isosceles triangle with fixed base ![]() are decreasing at the rate of
are decreasing at the rate of ![]() per second .how fast is the area decreasing when the two equal sides are equal to the base?
per second .how fast is the area decreasing when the two equal sides are equal to the base?
Answer : Let ![]() be isosceles where
be isosceles where ![]() is the base of fixed length b. Let the length of the two equal sides of
is the base of fixed length b. Let the length of the two equal sides of ![]() be ‘a’, draw
be ‘a’, draw ![]()
Now, in ![]() , by applying the Pythagoras theorem,
, by applying the Pythagoras theorem,
![]()
Area of triangle ![]()
The rate of change of the area with respect to time ![]() is given by,
is given by,
![]()
![]()
It is given that the two equal sides of the triangle are decreasing at the rate of ![]() per second.
per second.
![]()
![]()
Then, when ![]() we have:
we have:
![]()
Hence, if the two equal sides are equal to the base, then the area of the triangle is decreasing at the rate of ![]() .
.
Question 4: Find the equation of the normal to curve ![]() at the point
at the point ![]() .
.
Answer : The equation of the given curve is ![]() ,
,
Differentiating with respect to ![]() , we have
, we have
![]()
![]()
![]()
Now, the slope of the normal at point ![]() is
is ![]()
Equation of the normal at
![]() is
is ![]() i.e.
i.e. ![]() .
.
Question 5: Show that the normal at any point ![]() to the curve
to the curve
![]() is at a constant distance from the origin.
is at a constant distance from the origin.
Answer : We have ![]()
![]()
Since, ![]()
![]()
Now, ![]()
![]()
Slope of the normal= ![]()
The equation of the normal at a given point ![]() is given by,
is given by,
![]()
![]()
![]()
![]()
Now, the perpendicular distance of the normal from the origin is constant.
![]() , which is independent of
, which is independent of ![]() .
.
Hence, the perpendicular distance of the normal from the origin is constant.
Question 6: Find the intervals in which the function ![]() given by
given by ![]() is (i) Increasing (ii) Decreasing.
is (i) Increasing (ii) Decreasing.
Answer : ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now ![]() or
or ![]()
But ![]()
![]()
Now, ![]() and
and ![]() divides
divides ![]() into three disjoint intervals, i.e.
into three disjoint intervals, i.e.
![]()
In intervals ![]() and
and ![]() .
.
Thus, ![]() is increasing for
is increasing for ![]() and
and ![]() .
.
In the interval ![]() .
.
Thus, ![]() is decreasing for
is decreasing for ![]() .
.
Question 7: Find the intervals in which the function f given by ![]() is (i) increasing (ii) decreasing.
is (i) increasing (ii) decreasing.
Answer : ![]()
![]()
Then, ![]() i.e.
i.e. ![]()
![]()
Now, the points ![]() and
and ![]() divide the real line into three disjoint intervals i.e.,
divide the real line into three disjoint intervals i.e., ![]() and
and ![]()
In intervals ![]() and
and ![]() i.e., when
i.e., when ![]() and
and ![]()
Thus, when ![]() and
and ![]() is increasing.
is increasing.
In interval ![]() i.e., when
i.e., when ![]()
Thus, when ![]() is decreasing.
is decreasing.
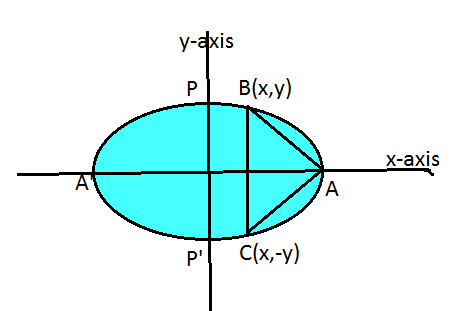
Question 8: Find the maximum area of an isosceles triangle inscribed in the ellipse ![]() with its vertex at one end of the major axis.
with its vertex at one end of the major axis.
Answer : The given ellipse is ![]() .
.
Let the major axis be along the ![]() -axis.
-axis.
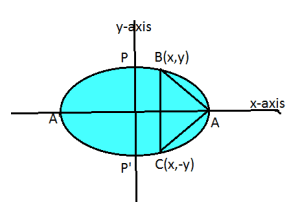
Let ![]() be the triangle inscribed in the ellipse where
be the triangle inscribed in the ellipse where
vertex ![]() is at
is at ![]() .
.
Let the point ![]()
![]()
![]() and
and ![]()
Area of ![]()
![]()
Squaring both side
![]()
Differntiate with respect to x
![]()
![]()
![]()
For max and minima ![]()
![]()
![]() or
or ![]()
![]() or
or ![]()
Since, ![]() is not possible
is not possible
Again differentiate of eq (ii)
![]()
![]()
At ![]()
![]()
![]()
Hence area of triangle is max when ![]()
Putting in eq (i)
Max area ![]()
![]()
![]()
Question 9: A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is ![]() and volume is
and volume is ![]() . If building of tank costs ₹70 per square meters for the base and ₹45 per square metre for sides. What is the cost of least expensive tank?
. If building of tank costs ₹70 per square meters for the base and ₹45 per square metre for sides. What is the cost of least expensive tank?
Answer : Let ![]() , and
, and ![]() represent the length, breadth, and height of the tank respectively.
represent the length, breadth, and height of the tank respectively.
Then, we have height ![]()
Volume of the ![]()
Volume of the tank ![]()
![]()
![]()
Now, area of the base ![]()
![]()
Total cost ![]()
![]()
![]()
Differentiate with respect to ‘l’
![]()
For max and minima ![]()
![]()
![]()
![]()
![]()
Again differentiate with respect to l
![]()
![]()
At ![]()
![]()
Therefore cost of tank is min when ![]()
Putting in (i)
minimum cost ![]()
![]()
![]()
Question 10: The sum of the perimeter of a circle and square is ![]() , where
, where ![]() is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
Answer : Let ![]() be the radius of the circle and
be the radius of the circle and ![]() be the side of the square. Then, we have:
be the side of the square. Then, we have:
![]() where
where ![]() is constant
is constant ![]()
![]()
The sum of the areas of the circle and the square ![]() is given by,
is given by,
![]()
![]()
Now ![]() .
.
![]()
![]()
![]()
![]()
Now, ![]() .
.
![]() When
When ![]()
![]() .
.
The sum of the area is least when ![]()
![]()
![]()
Hence, it has been proved that the sum of their areas is least when the side of the square is double the radius of the circle.
Question 11: A window is in the form of rectangle surmounted by a semicircular opening. The total perimeter of the window is ![]() . Find the dimensions of the window to admit maximum light through the whole opening
. Find the dimensions of the window to admit maximum light through the whole opening
Answer: Let ![]() and
and ![]() be the length and breadth of the rectangular window.
be the length and breadth of the rectangular window.
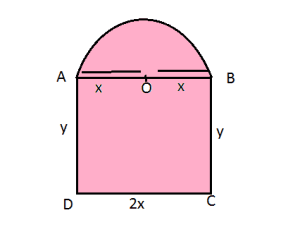
Radius of the semicircular opening ![]()
It is given that the perimeter of the window is ![]() .
.
![]()
![]()
![]()
Area of the window ![]() is given by,
is given by,
![]()
![]()
![]()
![]()
![]()
![]()
Now, ![]()
![]()
![]()
![]()
Thus, when ![]() then
then ![]() .
.
Therefore, by second derivative test, the area is the maximum when length ![]() .
.
Now, ![]()
![]()
Hence, the required dimensions of the window to admit maximum light is given by
Length ![]() and breath
and breath ![]() .
.
Question 12: A point on the hypotenuse of a triangle is at distance ![]() and
and ![]() from the sides of the triangle. Show that the minimum length of the hypotenuse is
from the sides of the triangle. Show that the minimum length of the hypotenuse is ![]()
Answer: Let ![]() be right-angled at
be right-angled at ![]() . Let
. Let ![]() and
and ![]() .
.
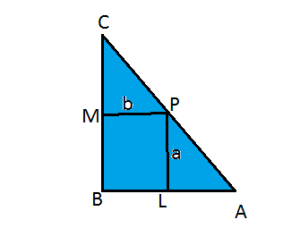
Let ![]() be a point on the hypotenuse of the triangle such that
be a point on the hypotenuse of the triangle such that ![]() is at a distance of
is at a distance of ![]() and
and ![]() from the sides
from the sides ![]() and
and ![]() respectively. Let
respectively. Let ![]()
We have, ![]()
Now, ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
It can be clearly shown that ![]() when
when ![]()
Therefore, by second derivative test, the length of the hypotenuse is minimum when ![]() .
.
Now, if ![]() , we have:
, we have:
![]()
![]()
Hence, the minimum length of the hypotenuses is ![]() .
.
Question 13: Find the points at which the function ![]() given by
given by ![]() has
has
(i) local maxima
(ii) local minima
(iii) point of inflexion.
Answer: The given function is ![]()
![]()
![]()
![]()
Now, ![]()
![]() and
and ![]() or
or ![]()
Now, for values of ![]() close to
close to ![]() and to the left of
and to the left of ![]() Also, for values of
Also, for values of ![]() close to
close to ![]() and to the right of
and to the right of ![]() .
.
Thus, ![]() is the point of local maxima.
is the point of local maxima.
Now, for values of ![]() close to 2 and to the left of
close to 2 and to the left of ![]() Also, for values of
Also, for values of ![]() close to 2 and to the right of
close to 2 and to the right of ![]() .
.
Thus, ![]() is the point of local minima.
is the point of local minima.
Now, as the value of ![]() varies through
varies through ![]() does not changes its sign.
does not changes its sign.
Thus, ![]() is the point of inflexion.
is the point of inflexion.
Question 14: Find the absolute maximum and minimum values of the function ![]() given by
given by
![]()
Answer: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now, evaluating the value of ![]() at critical points
at critical points ![]() and
and ![]() and at the end points of the interval
and at the end points of the interval ![]() (i.e., at
(i.e., at ![]() and
and ![]() ),
),
we have:
![]()
![]()
![]()
![]()
Hence, the absolute maximum value of ![]() is
is ![]() occurring at
occurring at ![]() and the absolute minimum value of
and the absolute minimum value of ![]() is 1 occurring at
is 1 occurring at ![]() and
and ![]() .
.
Question 15: Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius ![]() is
is ![]() .
.
Answer : Let ![]() be the centre and
be the centre and ![]() be the radius of the given sphere,
be the radius of the given sphere, ![]()
![]()
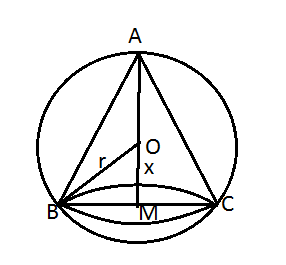
In ΔOBM, using pythagoras theorem
![]()
![]()
![]()
![]()
BM is the radius of cone
Volume of cone ![]()
![]()
![]()
![]()
Differentiating with respect to x
![]()
![]()
![]()
![]() —(ii)
—(ii)
For max and minima ![]()
![]()
Hence ![]() or
or ![]()
![]() or
or ![]()
![]() Not possible
Not possible
Agian differentiate with respect to x of eq (ii)
![]()
![]()
![]()
At ![]()
![]()
![]()
Hence volume of cone is max when ![]()
Height of cone ![]()
![]()
Question 16: Let ![]() be a function defined on
be a function defined on ![]() such that
such that ![]() , for all
, for all ![]() . Then prove that
. Then prove that ![]() is an increasing function on
is an increasing function on ![]() .
.
Answer : We have to prove that function is always increasing, i.e.
![]() for all
for all ![]() Where
Where ![]()
Let ![]() and
and ![]() be two numbers in the interval
be two numbers in the interval ![]() and
and ![]() .
.
Let the interval ![]() .
.
Function ![]() is continuous as well as differential in
is continuous as well as differential in ![]() as it is continuous and differential in
as it is continuous and differential in ![]() .
.
Using Mean value theorem, there exists ![]() , such that
, such that
![]()
Given that ![]() for all
for all ![]() .
.
Therefore, ![]() for all
for all ![]() .
.
![]()
![]()
Now, for the two point ![]() , where
, where ![]() , we have
, we have ![]() .
.
Hence, the functions ![]() is increasing in the interval
is increasing in the interval ![]() .
.
Question 17: Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius ![]() is
is ![]() . Also find the maximum volume.
. Also find the maximum volume.
Answer : Consider ![]() be the centre and
be the centre and ![]() be the radius of the given sphere,
be the radius of the given sphere, ![]()
![]()
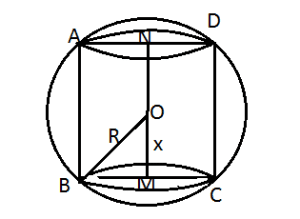
In ΔOBM, using pythagoras theorem
![]()
![]()
![]()
![]()
BM is the radius of cone
Volume of cone ![]()
![]()
Differentiating with respect to x
![]()
![]()
![]()
For max and minima ![]()
![]()
![]()
![]()
![]()
Again differentiate of eq (ii)
![]()
At ![]()
![]()
Therefore volume of cylinde is max when ![]()
Height of cylinder ![]()
Question 18: Show that the height of the cylinder of greatest volume which can be inscribed in a right circular cone of height ![]() and having semi vertical angle
and having semi vertical angle ![]() is one third that of the cone and the greatest volume of the cylinder is
is one third that of the cone and the greatest volume of the cylinder is ![]()
Solution: Let radius of cone = r and Radius of cylinder= x
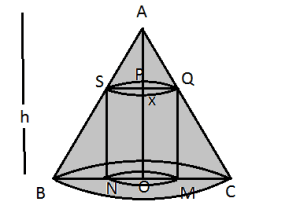
Semivertical angle of cone ![]() and height of cone
and height of cone ![]()
In ![]()
![]()
![]()
Therefore, Height of cylinder ![]()
![]()
Volume of cylinder ![]()
![]()
![]()
Differentiating with respect to ‘x’
![]()
![]()
For max and minima ![]()
![]()
![]()
![]()
![]()
Again differentiate with respect to x
![]()
At ![]()
![]()
![]()
Therefore the volume of cylinder is max when ![]()
Now from eq (i)
Height of cylinder ![]()
![]()
Volume of cylinder ![]()
![]()
![]()
Volume of cylinder ![]()
Question 19: A cylindrical tank of radius ![]() is being filled with wheat at the rate of 314 cubic meter per hour. Then the depth of wheat is increasing at the rate of:
is being filled with wheat at the rate of 314 cubic meter per hour. Then the depth of wheat is increasing at the rate of:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution: Option (A) is correct.
Consider ![]() be the depth of the wheat in the cylindrical tank whose radius is
be the depth of the wheat in the cylindrical tank whose radius is ![]() at time t.
at time t.
![]() Volume of wheat in cylindrical tank at time
Volume of wheat in cylindrical tank at time ![]() ,
,
So, ![]() cubic meter
cubic meter
We are given that ![]() cubic meter
cubic meter ![]()
So, ![]()
![]()
![]()
Therefore, ![]()
Question 20: The slope of the tangent to the curve ![]() at the point (2,
at the point (2, ![]() is:
is:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution: Option (B) is correct.
Solution: Equation of the curves are ![]() and
and ![]()
![]() and
and ![]() Slope of the tangent to the given curve at point
Slope of the tangent to the given curve at point ![]() is
is
![]()
At the given point ![]() and
and ![]()
At ![]() , from equation
, from equation ![]()
![]()
![]()
![]()
At ![]() , From eq(2)
, From eq(2) ![]()
![]()
![]()
![]()
![]()
Here, common value of ![]() in the two sets of values is 2 .
in the two sets of values is 2 .
Again, from equation (3),
Slope of the tangent to the given curve at point ![]()
Question 21: The line ![]() is a tangent to the curve
is a tangent to the curve ![]() if the value of
if the value of ![]() is:
is:
(A) 1
(B) 2
(C) 3
(D) ![]()
Solution: Option (A) is correct.
Equation of the curve is ![]()
![]()
![]()
Slope of the tangent to the given curve at point ![]()
![]()
![]()
![]()
Now ![]()
![]()
![]()
![]()
Putting the values of ![]() and
and ![]() in equation (1),
in equation (1), ![]()
![]()
Question 22: The normal at the point ![]() on the curve
on the curve ![]() is:
is:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution: Option (B) is correct.
Equation of the given curve is ![]()
![]()
![]()
Slope of the tangent to the given curve at point ![]() is
is
![]()
![]()
![]()
Equation of the normal at ![]() is
is ![]()
![]()
![]()
Question 23: The normal to the curve ![]() passing through
passing through ![]() is:
is:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution: Option ![]() is correct.
is correct.
Equation of the curve is ![]()
![]()
![]()
Slope of the normal at ![]() is
is
![]()
Again slope of normal at given point ![]()
From equation (2) and (3), we have ![]()
![]()
![]()
![]()
From equation (1),
![]()
![]()
![]()
![]()
Now, at point ![]() , slope of the normal from equation
, slope of the normal from equation ![]()
Equation of the normal is ![]()
![]()
or ![]()
Question 24: The points on the curve ![]() where the normal to the curve make equal intercepts with axes are:
where the normal to the curve make equal intercepts with axes are:
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
Solution: Option (A) is correct.
Equation of the curve is ![]()
![]()
![]()
Slope of the tangent to curve (1) at any point ![]() is
is
![]()
Slope of the normal ![]() .
.
Slopes of lines with equal intercepts on the axis are ![]()
So ![]()
if ![]()
![]()
From (i) and (ii) we have
![]() and
and ![]()
If ![]()
![]()
we have, ![]() and
and ![]()
Required points are ![]()