EXERCISE 7.4(Permutations and Combinations)

Exercise 7.4 ncert solutions maths class 11

Question 1: If ${ }^{\mathrm{n}} \mathrm{C}_8={ }^{\mathrm{n}} \mathrm{C}_2$ , find ${ }^{\mathrm{n}} \mathrm{C}_2$ .

Solution: Given that ${ }^n C_8={ }^n C_2$

We know that if ${ }^n C_r={ }^n C_p$ then either $r=p$ or $r=n-p$

If ${ }^n \mathrm{C}_8={ }^n \mathrm{C}_2$

$\Rightarrow 8=\mathrm{n}-2$

On rearranging we get

$\Rightarrow \mathrm{n}=10$

Now,

$\Rightarrow{ }^{10} \mathrm{C}_2=\frac{10 \times 9 \times 8 !}{2 \times 1 \times 8 !}$

$=\frac{90}{2}=45$

Question 2: Determine $n$ if

(i) ${ }^{2 n} C_{3:}{ }^n C_3=12: 1$

(ii) ${ }^{2 n} C_3:{ }^n C_3=11: 1$

Solution: (i) Given that: ${ }^{2 \mathrm{n}} \mathrm{C}_3:{ }^{\mathrm{n}} \mathrm{C}_3=12: 1$

$\Rightarrow \frac{2 \mathrm{n}_{\mathrm{C}_3}}{\mathrm{n}_{\mathrm{C}_3}}=\frac{12}{1}$

Substituting the formula we get

$\Rightarrow \dfrac{\frac{2 n !}{3 !(2 n-3) !}}{\frac{n !}{3 !(n-3) !}}=\frac{12}{1}$

$\Rightarrow \dfrac{\frac{2 n \times(2 n-1) \times(2 n-2) \times(2 n-3) !}{3 !(2 n-3) !}}{\frac{n \times(n-1) \times(n-2) \times(n-3) !}{3 !(n-3) !}}=\frac{12}{1}$

$\Rightarrow \dfrac{\frac{2 n \times(2 n-1) \times(2 n-2)}{3 !}}{\frac{n \times(n-1) \times(n-2)}{3 !}}=\frac{12}{1}$

$\Rightarrow \dfrac{2 \mathrm{n} \times(2 \mathrm{n}-1) \times(2 \mathrm{n}-2)}{\mathrm{n} \times(\mathrm{n}-1) \times(\mathrm{n}-2)}=\frac{12}{1}$

$\Rightarrow \dfrac{2 \mathrm{n} \times(2 \mathrm{n}-1) \times 2 \times(n-1)}{\mathrm{n} \times(\mathrm{n}-1) \times(n-2)}=\frac{12}{1}$

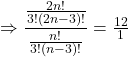
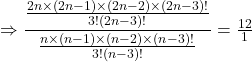
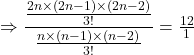
On multiplying we get

$\Rightarrow \frac{4 \times n \times(2 n-1)}{n \times(n-2)}=\frac{12}{1}$

$\Rightarrow \frac{4 \times(2 n-1)}{(n-2)}=\frac{12}{1}$

$\Rightarrow 4 \times(2 n-1)=12 \times(n-2)$

$\Rightarrow 8 n-4=12 n-24$

$\Rightarrow 12 n-8 n=24-4$

$\Rightarrow 4 n=20$

$\therefore n=5$

(ii) Given that: ${ }^{2 \mathrm{n}} \mathrm{C}_3:{ }^{\mathrm{n}} \mathrm{C}_3=11: 1$

$\Rightarrow \frac{2 n_{C_3}}{\mathrm{n}_{C_3}}=\frac{12}{1}$

$\Rightarrow \dfrac{\frac{2 n !}{3 !(2 n-3) !}}{\frac{n !}{3 !(n-3) !}}=\frac{12}{1}$

$\Rightarrow \dfrac{\frac{2 n \times(2 n-1) \times(2 n-2) \times(2 n-3) !}{3 !(2 n-3) !}}{\frac{n \times(n-1) \times(n-2) \times(n-3) !}{3 !(n-3) !}}=\frac{11}{1}$

$\Rightarrow \dfrac{\frac{2 n \times(2 n-1) \times(2 n-2)}{3 !}}{\frac{n \times(n-1) \times(n-2)}{3 !}}=\frac{11}{1}$

$\Rightarrow \frac{2 \mathrm{n} \times(2 n-1) \times(2 n-2)}{n \times(n-1) \times(n-2)}=\frac{11}{1}$

$\Rightarrow \frac{2 \mathrm{n} \times(2 n-1) \times 2 \times(n-1)}{n \times(n-1) \times(n-2)}=\frac{11}{1}$

$\Rightarrow \frac{4 \times \mathrm{n} \times(2 n-1)}{\mathrm{n} \times(n-2)}=\frac{11}{1}$

$\Rightarrow \frac{4 \times(2 n-1)}{(n-2)}=\frac{11}{1}$

$\Rightarrow 4 \times(2 n-1)=11 \times(n-2)$

$\Rightarrow 8 \mathrm{n}-4=11 \mathrm{n}-22$

$\Rightarrow 11 n-8 n=22-4$

$\Rightarrow 3 n=18$

$\therefore n=6$

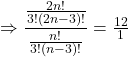
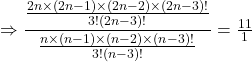
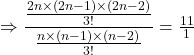
Question 3; How many chords can be drawn through 21 points on a circle?

Solution: Given 21 points on a circle and we require two points on the circle to draw a chord

$\therefore$ Number of chords is are

$\Rightarrow{ }^{21} \mathrm{C}_2=\frac{21 !}{2 !(21-2) !}$

$=\frac{21 \times 20 \times 19 !}{2 ! \times 19 !}$

$=\frac{21 \times 20}{2 \times 1}$

$=\frac{420}{2}=210$

$\therefore$ Total number of chords can be drawn are 210

Question 4: In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?

Solution: Given 5 boys and 4 girls are in total

We can select 3 boys from 5 boys in ${ }^5 C_3$ ways

Similarly, we can select 3 boys from 4 girls in ${ }^4 C_3$ ways

$\therefore$ Number of ways a team of 3 boys and 3 girls can be selected = ${ }^5 C_3 \times{ }^4 C_3$

$\Rightarrow{ }^5 C_3 \times{ }^4 C_3$

$=\frac{5 !}{3 !(5-3) !} \times \frac{4 !}{3 !(4-3) !}$

$=\frac{5 !}{3 ! \times 2 !} \times \frac{4 !}{3 ! \times 1 !}$

$\Rightarrow{ }^5 C_3 \times{ }^4 C_3$

$=10 \times 4=40$

$\therefore$ Number of ways a team of 3 boys and 3 girls can be selected is ${ }^5 C_3 \times{ }^4 C_3=40$ ways

Question 5: Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.

Solution: Given 6 red balls, 5 white balls and 5 blue balls

We can select 3 red balls from 6 red balls in ${ }^6 C_3$ ways

Similarly, we can select 3 white balls from 5 white balls in ${ }^5 C_3$ ways

Similarly, we can select 3 blue balls from 5 blue balls in ${ }^5 C_3$ ways

$\therefore$ Number of ways of selecting 9 balls is ${ }^6 \mathrm{C}_3 \times{ }^5 \mathrm{C}_3 \times{ }^5 \mathrm{C}_3$

$\Rightarrow{ }^6 C_3 \times{ }^5 C_3 \times{ }^5 C_3$

$=\frac{6 !}{3 !(6-3) !} \times \frac{5 !}{3 !(5-3) !} \times \frac{5 !}{3 !(5-3) !}$

$=\frac{6 !}{3 ! \times 3 !} \times \frac{5 !}{3 ! \times 2 !} \times \frac{5 !}{3 ! \times 2 !}$

$\Rightarrow{ }^6 C_3 \times{ }^5 C_3 \times{ }^5 C_3$

$=\frac{6 \times 5 \times 4 \times 3 !}{3 ! \times 3 !} \times \frac{5 \times 4 \times 3 !}{3 ! \times 2 !} \times \frac{5 \times 4 \times 3 !}{3 ! \times 2 !}$

$=\frac{120}{3 \times 2 \times 1} \times \frac{20}{2 \times 1} \times \frac{20}{2 \times 1}=20 \times 10 \times 10=2000$

$\therefore$ Number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour = ${ }^6 C_3 \times{ }^5 C_3 \times{ }^5 C_3=2000$

Question 6: Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.

Solution: Given a deck of 52 cards

There are 4 Ace cards in a deck of 52 cards. According to question, we need to select 1 Ace card out the 4 Ace cards

$\therefore$ Number of ways to select 1 Ace from 4 Ace cards is ${ }^4 \mathrm{C}_1$

$\Rightarrow$ More 4 cards are to be selected now from 48 cards (52 cards -4 Ace cards)

$\therefore$ Number of ways to select 4 cards from 48 cards is ${ }^{48} \mathrm{C}_4$

$\Rightarrow{ }^4 \mathrm{C}_1 \times{ }^{48} \mathrm{C}_4$

$=\frac{4 !}{1 !(4-1) !} \times \frac{48 !}{4 !(48-4) !}$

$=\frac{4 !}{1 ! \times 3 !} \times \frac{48 !}{4 ! \times 44 !}$
$\Rightarrow{ }^4 \mathrm{C}_1 \times{ }^{48} \mathrm{C}_4$

$=\frac{4 \times 3 !}{1 ! \times 3 !} \times \frac{48 \times 47 \times 46 \times 45 \times 44 !}{4 ! \times 44 !}$

$=\frac{4}{1} \times \frac{4669920}{24}$

$=4 \times 194580=778320$

$\therefore$ Number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination = 778320.

Question 7: In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?

Solution: Given 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers

There are 5 players who bowl, and we can require 4 bowlers in a team of 11

$\therefore$ Number of ways in which bowlers can be selected are: ${ }^5 \mathrm{C}_4$

Now other players left are $=17-5$ (bowlers) $=12$

Since we need 11 players in a team and already 4 bowlers are selected, we need to select 7 more players from 12 .

$\therefore$ Number of ways we can select these players are: ${ }^{12} C_7$

$\therefore$ Total number of combinations possible are: ${ }^5 \mathrm{C}_4 \times{ }^{12} \mathrm{C}_7$

$\Rightarrow{ }^5 \mathrm{C}_4 \times{ }^{12} \mathrm{C}_7$

$=\frac{5 !}{4 !(5-4) !} \times \frac{12 !}{7 !(12-7) !}=\frac{5 !}{4 ! \times 1 !} \times \frac{12 !}{7 ! \times 5 !}$

$\Rightarrow{ }^5 \mathrm{C}_4 \times{ }^{12} \mathrm{C}_7$

$=\frac{5 \times 4 !}{1 ! \times 4 !} \times \frac{12 \times 11 \times 10 \times 9 \times 8 \times 7 !}{5 ! \times 7 !}$

$=\frac{5}{1} \times \frac{95040}{120}$

$=5 \times 792=3960$

$\therefore$ Number of ways we can select a team of 11 players where 4 players are bowlers from 17 players = 3960

Question 8: A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.

Solution: Given a bag contains 5 black and 6 red balls
Number of ways we can select 2 black balls from 5 black balls are ${ }^5 \mathrm{C}_2$

Number of ways we can select 3 red balls from 6 red balls are ${ }^6 C_3$

Number of ways 2 black and 3 red balls can be selected = ${ }^5 \mathrm{C}_2 \times{ }^6 \mathrm{C}_3$

$\therefore{ }^5 \mathrm{C}_2 \times{ }^6 \mathrm{C}_3=\frac{5 !}{2 !(5-2) !} \times \frac{6 !}{3 !(6-3) !}$

$=\frac{5 !}{2 ! \times 3 !} \times \frac{6 !}{3 ! \times 3 !}$

$\Rightarrow{ }^5 \mathrm{C}_2 \times{ }^6 \mathrm{C}_3$

$=\frac{5 \times 4 \times 3 !}{2 ! \times 3 !} \times \frac{6 \times 5 \times 4 \times 3 !}{3 ! \times 3 !}$

$=\frac{20}{2} \times \frac{120}{6}$

$=10 \times 20=200$

$\therefore$ Number of ways in which 2 black and 3 red balls can be selected from 5 black and 6 red balls are 200

Question 9: In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?

Solution: Given 9 courses are available and 2 specific courses are compulsory for every student Here 2 courses are compulsory out of 9 courses, so a student need to select 5 – $2=3$ courses