Class 10 Chapter 2(Poloynomials)

Case based 2:

While passing over an iron bridge, Hema noticed that the shape resembles a curve about which she had studied in mathematics.(Class 10 Case based problem of Chapter 2 Polynomials 2)

(A) What type of ploynomial does the shape of the bridge represents ?

(B) Find the zeroes of the polynomial x² + 7x – 60

Solution: (A) The shape of the bridge represents quadratic polynomial

(B) To find the zeros of the polynomial x² + 7x – 60, we need to factorize the polynomial.

x² + 7x – 60 = x²  + 12x – 5x – 60

=  x(x + 12) -5(x + 12)

=  (x + 12)(x – 5)

Therefore zeros of the polynomial  = 5 , -12

Case based 3:

Due to heavy storm, an electric wire got bent as shown in the figure. It followed a mathematical shape. Answer the following question below:

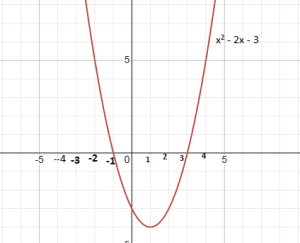
(A) Name the shape in which the wire is bent.

(a) Spiral                 (b) Ellipse

(c) Linear                 (d) Parabola

(B) How many zeros are there for the polynomaial(shape of the wire)

(a) 2                           (b) 3

(c) 1                             (d) 0

(C) The zeros of the polynomial are

(a) -1, 5                      (b) -1, 3

(c) 3, 5                        (d)  -4, 2

(D) What will be the expression of the polynomial?

(a) x² + 2x – 3             (b) x² – 2x + 3

(c) x² – 2x – 3               (d) x² + 2x + 3

(E) What is the value of the polynomial if x = -1?

(a) 6                              (b) -18

(c) 18                            (d) 0

Solution:

(A) Answer (d) Parabola

(B) Answer (a) 2

Explanation:

Graph of the polynomial intersect x-axis at two points

Hence, number of zeroes  of the polynomial  = 2

(C) Answer (b) -1, 3

Explanation:

We know, points at which graph of a polynomial intersect the x- axis,are the zeros of the polynomial. Here, The graph intersects x-axis at points -1 and 3

Its zeros are = -1 and 3

(D) Answer (c) x² – 2x – 3

Explanation:

We have the zeros of the polynomial are -1 and 3

Then quadratic equation is

= x² – (Sum of zeroes) x + Product of zeroes

= x² – (-1 + 3)x + (-1)(3)

= x² – 2x – 3

Some other question

Question 1:Prove that 2-√3 is irrational, given that root 3 is irrational

Question 2:Prove that √5 is an irrational number

Question 3: Prove that  √p + √q is irrational

Question 4:Prove that root 2 + root 5 is irrational

gmath.in