Fast revision(Math)
class 12 revision of cbse math part-I 2022-2023
Class 12 revision of cbse math part-II 2022-2023

Integration: Chapter 7
Exercise 7.1
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
(9) ![]()
(10) ![]()
(11) ![]()
(12) ![]()
(13) ![]()
(14) ![]()
(15) ![]()
(16) ![]()
(17) ![]()
(18) ![]()
Methods of Integration:-
1. Integration by Substitution
2. Integration using Partial Fractions
3. Integration by Parts
Exercise 7.2
Integration by substitution
⇒ Some other formulae:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
Exercise 7.3
Integration using trigonometric identities
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
(9) ![]()
(10)(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(11) (a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
Exercise 7.4
Integrals of Some Particular Functions
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
(8) ![]()
(9) ![]()
![]()
![]()
(10) ![]()
From (7) to (10) types form using completing the square
![]() for completing the square add and subtract by
for completing the square add and subtract by ![]()
Exercise 7.5
Integration by Partial Fractions:
⇒ Partial fraction expression:
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
Exercise 7.6
Integration by Parts
Formula
(1) ![]()
ILATE
I= inverse tigonometry(![]() )
)
L= logrithmic function(![]() )
)
A= Algebraic function
T = trigonometric function
E= Exponential function
(2) ![]()
Exercise 7.7
Integrals of some more types
(1) ![]()
(2) ![]()
(3) ![]()
Exercise 7.9 & 7.10
![]()
Evaluation of Definite Integrals by Substitution
Exercise 7.11
Some Properties of Definite Integrals
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
(7) ![]()
![]()
(8) ![]()
![]()
Chapter 8
Area under Simple Curves
Area of region when strip is perpendicular to x-axis ![]()
Area of region when strip is perpendicular to x-axis ![]()
Exercise 8.2
Area between Two Curves ![]() when
when ![]()
Chapter 9(Differential equation): Exercise 9.1:
Order of a differential equation:-Order of a differential equation is defined as the order of the highest order derivative of the dependent variable with respect to the independent variable involved in the given differential equation.
Ex:-![]()
Order of d.e. = 2
Degree of a differential equation:-By the degree of a differential equation, when it is a polynomial equation in
derivatives, we mean the highest power (positive integral index) of the highest order derivative involved in the given differential equation.
EX:- ![]()
Degree of d.e. = 3
NOTE:- Order and degree (if defined) of a differential equation are always positive integers.
Exercise 9.2
General solution:The solution which contains arbitrary constants is called the general solution(primitive) of the differential equation.
particular solution:-The solution free from arbitrary constants i.e., the solution obtained from the general solution by giving particular values to the arbitrary constants is called a particular solution of the differential equation.
Methods of Solving First Order, First Degree Differential Equations
Exercise 9.4
Differential equations with variables separable
Exercise: 9.5
Homogeneous differential equations:- In homogeneous differential equation substitute ![]() or
or ![]()
Exercise 9.6
Linear differential equations:-
(1) (i) Write the given differential equation in the form ![]() where P, Q are constants or functions of x only.
where P, Q are constants or functions of x only.
(ii) Find the Integrating Factor ![]()
(iii) Solution of differential equation of this form is
![]()
(2) (i) Write the given differential equation in the form ![]() where P, Q are constants or functions of x only.
where P, Q are constants or functions of x only.
(ii) Find the Integrating Factor ![]()
(iii) Solution of differential equation of this form is
![]()
Vector algebra:
Exercise 10.1
Let The point P(x, y, z)
Position vector of P
![]()
dr’s of line OP = (x, y, z)
dc’s of the line OP
![]()
Relation between dc’s
![]()
Types of Vectors:
(1) Zero Vector: A vector whose initial and terminal points coincide, is called a zero vector (or null vector)
Ex:- ![]()
(2) Unit Vector: A vector whose magnitude is unity (i.e., 1 unit) is called a unit vector. The unit vector in the direction of ![]() given vector is denoted by
given vector is denoted by ![]() .
.
(3) Coinitial Vectors: Two or more vectors having the same initial point are called coinitial vectors.
(4) Collinear Vectors :Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.
(5) Equal Vectors: Two vectors ![]() and
and ![]() are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points, and written
are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points, and written
as ![]() .
.
(6) Negative of a Vector :-A vector whose magnitude is the same as that of a given vector (say, ![]() ), but direction is opposite to that of it, is called negative of the given vector.
), but direction is opposite to that of it, is called negative of the given vector.
For example, ![]() vector is negative of the vector
vector is negative of the vector ![]() , and written as
, and written as ![]() .
.
Exercise 10.2
Let ![]()
(i) Modulus of ![]()
![]()
(ii) Unit vector:- ![]()
![]()
Components of a vector:
Let ![]()
Scalar component of ![]()
Vector component of ![]()
Remarks:
![]() and
and ![]()
(i) Let two vectors ![]() and
and ![]() are collinear vector
are collinear vector
![]()
(ii) If ![]() , then
, then ![]() are also called direction ratios of .
are also called direction ratios of .
(iii) In case if it is given that l, m, n are direction cosines of a vector, then ![]() is the unit vector in the direction of that vector, where
is the unit vector in the direction of that vector, where ![]() and
and ![]() are the angles which the vector makes with x, y and z axes respectively.
are the angles which the vector makes with x, y and z axes respectively.
Vector joining two points:
If ![]() and
and ![]() are any two points, then the vector joining
are any two points, then the vector joining ![]() and
and ![]() is the
is the
vector ![]()
![]()
![]()
Then, ![]()
![]()
![]()
Magnitude of ![]() is
is ![]()
Section formula: P and q are two points on line and point R divide PQ in m:n Then
![]()
And the mid point
![]()
Product of Two Vectors
Scalar (or dot) product of two vectors: The scalar product of two nonzero vectors ![]() and
and ![]() , denoted by
, denoted by ![]()
![]()
Observation: (1) Let ![]() and
and ![]() be two nonzero vectors, then
be two nonzero vectors, then ![]() if and only if
if and only if ![]() and
and ![]() are perpendicular to each other. i.e.
are perpendicular to each other. i.e.
![]()
(2) If ![]() then,
then, ![]()
In particular, ![]() in this case
in this case ![]()
(3) If ![]() then,
then, ![]()
(4) ![]()
![]()
(5) 
(6) The scalar product is commutative, i.e.
![]()
(7) If ![]() and
and ![]()
Then ![]()
Projection of a vector on a line
Projection of a vector ![]() on other vector
on other vector ![]() , is given by
, is given by
![]() or
or  or
or ![]()
Remarks: ![]()
![]()
Vector (or cross) product of two vectors
(1) ![]() is vector.
is vector.
(2) Let ![]() and
and ![]() be two non zero vectors, then
be two non zero vectors, then ![]() if and only if
if and only if ![]() and
and ![]() are parallel(or collinear)to each other i.e.
are parallel(or collinear)to each other i.e.
![]()
In Particular ![]()
(3). If ![]() and
and ![]() .
.
(4) ![]()
(5) ![]()
(6) 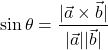
(7) ![]()
(8) ![]()
(9) If ![]() and
and ![]() are the adjacent sides of a triangle then its area is given as
are the adjacent sides of a triangle then its area is given as ![]()
(10) If ![]() and
and ![]() are the adjacent sides of a parallelogram then its area is given as
are the adjacent sides of a parallelogram then its area is given as ![]()
(11) If ![]() and
and ![]()
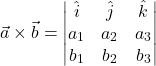
Three dimension geometry
Direction cosine: If ![]() makes angles
makes angles ![]() with x, y, and z-axis respectively
with x, y, and z-axis respectively
![]()
![]()
Relation between direction cosine of a line
![]()
Direction cosines of a line passing through two points:
Let ![]() and
and ![]()
Then ![]()
![]()
![]()
Equation of a Line in Space:
(i) it passes through a given point and has given direction,
(ii) it passes through two given points.
Equation of a line through a given point and parallel to a given vector $\vec{b}$
vector form:
![]()
Cartesian form:
If point ![]() and direction ratio =
and direction ratio = ![]()
![]()
Note: –If l, m, n are the direction cosines of the line, the equation of the line is
![]()
Equation of a line passing through two given points:
Two points are ![]() and
and ![]() then equation of line
then equation of line
![]()
In cartesian form:
Two points ![]() and
and ![]()
Equation of line
![]()
Angle between Two Lines:
![]() and
and ![]() angle between them is
angle between them is ![]()
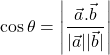
Or
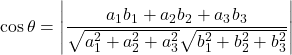
(i) If the lines are perpendicular, ![]()
![]() or
or ![]()
(ii) If two lines are parallel ![]() or
or ![]()
![]()
Shortest Distance between Two Lines
(i) Distance between two skew lines
![]()
![]()
Shortest distance=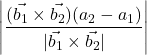
In cartesian form:
![]()
![]()

(ii) Distance between parallel lines
![]()
![]()
Distance 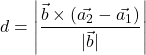
Linear Programming Problems
Constraints
![]()
![]()
Objective function;
![]()
![]() are called decision variables
are called decision variables
Max or min value of Z is called optimal value
Probability:-
(i)![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
(vi) ![]()
Exercise 13.1
Conditional Probability:
![]()
Properties of conditional probability:- Let E and F be events of a sample space S of an experiment, then we have
(a) ![]()
(b) ![]()
(c) ![]()
Exercise 13.2
Multiplication Theorem on Probability:-
(i) ![]()
(ii) ![]()
![]()
Independent Events: ![]()
Bayes’ Theorem:- ![]() and
and ![]() are three events and A be a non zero events
are three events and A be a non zero events
![]()
Theorem of total probability:-
![]()
Mean ![]()

