Exercise 5.1 (Continuity and Differentiability)
Question 1: Prove that the function ![]() is continuous at
is continuous at ![]() and at
and at ![]() . (Class 12 ncert solution math exercise 5.1)
. (Class 12 ncert solution math exercise 5.1)
Solution: The given function is ![]()
At ![]()
![]()
![]()
Therefore, ![]() is continous at
is continous at ![]() .
.
![]()
![]()
![]()
Therefore, ![]() is continous at
is continous at ![]() .
.
![]()
![]()
![]()
Therefore, ![]() is continous at
is continous at ![]() .
.
Question 2: Examine the continuity of the function ![]() at
at ![]() .
.
Solution:The given function is ![]()
At ![]()
![]()
![]()
Therefore, ![]() is continous at
is continous at ![]() .
.
Question 3: Examine the following functions for continuity.
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
Solution:(i) The given function is ![]()
It is evident that ![]() is defined at every real number
is defined at every real number ![]() and its value at
and its value at ![]() is
is ![]() .
.
It is also observed that
![]()
![]()
Hence, ![]() is continuous at every real number and therefore, it is a continuous function.
is continuous at every real number and therefore, it is a continuous function.
(ii) The given function is ![]() For any real number
For any real number ![]() , we obtain
, we obtain
![]()
Also,
![]()
![]()
Hence, ![]() is continuous at every point in the domain of
is continuous at every point in the domain of ![]() and therefore, it is a continuous function.
and therefore, it is a continuous function.
(iii) The given function is ![]()
For any real number ![]() , we obtain
, we obtain
![]()
![]()
Also,
![]()
![]()
Hence, ![]() is continuous at every point in the domain of
is continuous at every point in the domain of ![]() and therefore, it is a continuous function.
and therefore, it is a continuous function.
(iv) The given function is 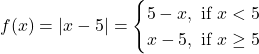
This function ![]() is defined at all points of the real line. Let
is defined at all points of the real line. Let ![]() be a point on a real line. Then,
be a point on a real line. Then, ![]() or
or ![]()
Case I: ![]()
Then, ![]()
![]()
![]()
Therefore, ![]() is continuous at all real numbers less than 5 .
is continuous at all real numbers less than 5 .
Case II: ![]()
Then, ![]()
![]()
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]()
Case III: ![]()
Then, ![]()
![]()
![]()
Therefore, ![]() is continuous at all real numbers greater than 5 .
is continuous at all real numbers greater than 5 .
Hence, ![]() is continuous at every real number and therefore, it is a continuous function.
is continuous at every real number and therefore, it is a continuous function.
Question 4: Prove that the function ![]() is continuous at
is continuous at ![]() , where
, where ![]() is a positive integer.
is a positive integer.
Solution: The given function is ![]()
It is observed that ![]() is defined at all positive integers,
is defined at all positive integers, ![]() , and its value at
, and its value at ![]() is
is ![]() .
.
Then,
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() , where
, where ![]() is a positive integer.
is a positive integer.
Question 5: Is the function ![]() defined by
defined by 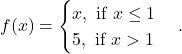 continuous at
continuous at ![]() At
At ![]() At
At ![]()
Solution: The given function is ![]()
At ![]() ,
,
It is evident that ![]() is defined at 0 and its value at 0 is 0 .
is defined at 0 and its value at 0 is 0 .
Then,
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
At ![]() ,
,
It is evident that ![]() is defined at 1 and its value at 1 is 1 .
is defined at 1 and its value at 1 is 1 .
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
![]()
Therefore, ![]() is not continuous at
is not continuous at ![]() .
.
At ![]() ,
,
It is evident that ![]() is defined at 2 and its value at 2 is 5 .
is defined at 2 and its value at 2 is 5 .
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
Question 6: Find all points of discontinuity of ![]() , where
, where ![]() is defined by
is defined by ![]()
Solution: The given function is 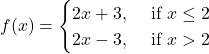
It is evident that the given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line. Then three case arise
be a point on the real line. Then three case arise
Case I: ![]()
Case II: ![]()
Case III: ![]()
Case I: ![]()
![]()
Then,
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: ![]()
Then,
![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]()
Case III: ![]()
Then, the left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at ![]() do not coincide.
do not coincide.
Therefore, ![]() is not continuous at
is not continuous at ![]() .
.
Hence, ![]() is the only point of discontinuity of
is the only point of discontinuity of ![]() .
.
Question 7:Find all points of discontinuity of ![]() , where
, where ![]() is defined by
is defined by
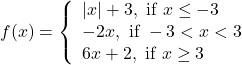
Solution:The given function is
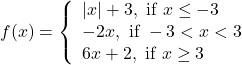
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line.
be a point on the real line.
Case I:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II:
If ![]() , then
, then ![]()
![]()
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
Case III:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous in
is continuous in ![]() .
.
Case IV:If ![]() , then the left hand limit of
, then the left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at ![]() do not coincide. Therefore,
do not coincide. Therefore, ![]() is not continuous at
is not continuous at
![]() .
.
Case V:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Hence, ![]() is the only point of discontinuity of
is the only point of discontinuity of ![]() .
.
Question 8:Find all points of discontinuity of ![]() , where
, where ![]() is defined by
is defined by
![]()
Solution: The given function is
![]()
It is known that, ![]() and
and ![]()
Therefore, the given function can be rewritten a
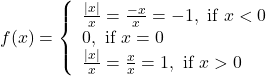
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line.
be a point on the real line.
Case I:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() .
.
Case II:If ![]() , then the left hand limit of
, then the left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at ![]() do not coincide.
do not coincide.
Therefore, ![]() is not continuous at
is not continuous at ![]() .
.
Case III:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Hence, ![]() is the only point of discontinuity of
is the only point of discontinuity of ![]() .
.
Question 9:Find all points of discontinuity of ![]() , where
, where ![]() is defined by
is defined by
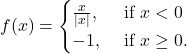
Solution: ![]()
The given function is
It is known that ![]()
Therefore, the given function can be rewritten as
![]()
![]()
Let ![]() be any real number.
be any real number.
Then, ![]()
Also, ![]()
Therefore, the given function is a continuous function.
Hence, the given function has no point of discontinuity.
Question 10:Find all points of discontinuity of ![]() , where
, where ![]() is defined by
is defined by ![]()
Solution: The given function is ![]()
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line.
be a point on the real line.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Hence, the given function ![]() has no point of discontinuity.
has no point of discontinuity.
Question 11: Find all points of discontinuity of ![]() , where
, where ![]() is defined by
is defined by ![]()
Solution: The given function is ![]()
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line.
be a point on the real line.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then
, then ![]()
![]()
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Thus, the given function ![]() is continuous at every point on the real line.
is continuous at every point on the real line.
Hence, ![]() has no point of discontinuity.
has no point of discontinuity.
Question 12: Find all points of discontinuity of ![]() , where
, where ![]() is defined by
is defined by
![]()
Solution: The given function is
![]()
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line.
be a point on the real line.
Case I:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then the left hand limit of
, then the left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at ![]() do not coincide.
do not coincide.
Therefore, ![]() is not continuous at
is not continuous at ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Thus from the above observation, it can be concluded that ![]() is the only point of discontinuity of
is the only point of discontinuity of ![]() .
.
Question 13: Is the function defined by ![]() a continous function?
a continous function?
Solution: The given function is 
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line.
be a point on the real line.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is, ![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at ![]() do not coincide.
do not coincide.
Therefore, ![]() is not continuous at
is not continuous at ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
From the above observation it can be concluded that, ![]() is the only point of discontinuity of
is the only point of discontinuity of ![]() .
.
Question 14: 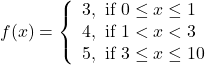
Discuss the continuity of the function ![]() , where
, where ![]() is defined by
is defined by
Solution: The given function is 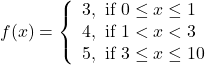
The given function ![]() is defined at all the points of the interval
is defined at all the points of the interval ![]() .
.
Let ![]() be a point in the interval
be a point in the interval ![]() .
.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous in the interval
is continuous in the interval ![]() .
.
Case II: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at ![]() do not coincide.
do not coincide.
Therefore, ![]() is not continuous at
is not continuous at ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at in the interval
is continuous at in the interval ![]() .
.
Case IV: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at ![]() do not coincide. Therefore,
do not coincide. Therefore, ![]() is discontinuous at
is discontinuous at ![]() .
.
Case V:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points of the interval
is continuous at all points of the interval ![]() .
.
Hence, ![]() is discontinuous at
is discontinuous at ![]() and
and ![]() .
.
Question 15: 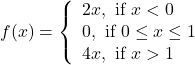
Solution: The given function is 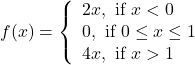
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Case I: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]()
Case II: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at
![]() do not coincide.
do not coincide.
Therefore, ![]() is not continuous at
is not continuous at ![]() .
.
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , except
, except ![]() .
.
Question 16: Discuss the continuity of the function ![]() , where
, where ![]() is defined by
is defined by
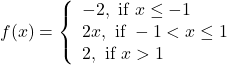
Solution: The given function is
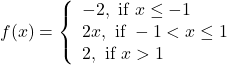
The given function ![]() is defined at all the points.
is defined at all the points.
Case I: If ![]() , then
, then ![]()
herefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]()
Case III: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Thus, from the above observations, it can be concluded that ![]() is continuous at all points of the real line.
is continuous at all points of the real line.
Question 17: Find the relationship between ![]() and
and ![]() so that the function
so that the function ![]() defined by
defined by ![]() is continous at
is continous at ![]() .
.
Solution: The given function is 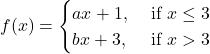
For ![]() to be continuous at
to be continuous at ![]() , then
, then
![]()
Also,
![]()
![]()
![]()
Therefore, from (1), we obtain
![]()
![]()
![]()
![]()
Therefore, the required relationship is given by, ![]() .
.
Question 18: For what value of ![]() is the function defined by
is the function defined by ![]() is continous at
is continous at ![]() What about continuity at
What about continuity at ![]()
Solution: The given function is
![]()
If ![]() is continuous at
is continuous at ![]() , then
, then
![]()
![]()
![]()
![]()
Therefore, there is no value of ![]() for which
for which ![]() is
is
continuous at ![]() .
.
At x=1
f(1)=4 x+1=4(1)+1=5
![]()
![]()
Therefore, for any values of ![]() is continuous at
is continuous at ![]() .
.
Question 19: Show that the function defined by ![]() is discontinuous at all integral point. Here
is discontinuous at all integral point. Here ![]() denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to ![]() .
.
Solution: The given function is ![]()
It is evident that ![]() is defined at all integral points.
is defined at all integral points.
Let ![]() be an integer.cuemath
be an integer.cuemath
Then,
![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
It is observed that the left and right hand limit of ![]() at
at ![]() do not coincide.
do not coincide.
Therefore, ![]() is not continuous at
is not continuous at ![]() .
.
Hence, ![]() is discontinuous at all integral points.
is discontinuous at all integral points.
Question 20: Is the function defined by ![]() continuous at
continuous at ![]() ?
?
Solution: The given function is ![]()
It is evident that ![]() is defined at
is defined at ![]() .
.
At ![]()
Consider ![]()
Put ![]() , it is evident that if
, it is evident that if ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the given function ![]() is continuous at
is continuous at ![]() .
.
Question 21: Discuss the continuity of the following functions.
(i) ![]()
(ii) ![]()
(iii) ![]()
Solution: It is known that if ![]() and
and ![]() are two continuous functions, then
are two continuous functions, then ![]() and
and ![]() are also continuous.
are also continuous.
Let ![]() and
and ![]() are continuous functions.
are continuous functions.
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number. Put
be a real number. Put ![]()
If ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, ![]() is a continuous function.
is a continuous function.
Let ![]()
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number. Put
be a real number. Put ![]()
If ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, ![]() is a continuous function.
is a continuous function.
Therefore, it can be concluded that,
(i) ![]() is a continuous function.
is a continuous function.
(ii) ![]() is a continuous function.
is a continuous function.
(iii) ![]() is a
is a
continuous function.
Question 22: Discuss the continuity of the cosine, cosecant, secant, and cotangent functions.
Solution: It is known that if ![]() and
and ![]() are two continuous functions, then
are two continuous functions, then
![]()
is continuous.
![]()
is continuous.
![]()
is continuous.
Let ![]() and
and ![]() are continuous functions.
are continuous functions.
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number. Put
be a real number. Put ![]()
If ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, ![]() is a continuous function.
is a continuous function.
Let ![]()
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number. Put
be a real number. Put ![]()
If ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, ![]() is a continuous function.
is a continuous function.
Therefore, it can be concluded that, ![]() is continuous.
is continuous.
![]() is continuous.
is continuous.
Therefore, cosecant is continuous except at ![]()
![]() is continuous.
is continuous.
![]() is continuous.
is continuous.
Therefore, secant is continuous except at ![]()
![]() is continuous.
is continuous. ![]() is continuous.
is continuous.
Therefore, cotangent is continuous except at ![]() .
.
Question 23: ![]()
Find the points of discontinuity of ![]() , where
, where
Solution: The given function is 
The given function ![]() is defined at all the points of the real line. Let
is defined at all the points of the real line. Let ![]() be a point on the real line.
be a point on the real line.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case III: If ![]() , then
, then ![]()
The left hand limit of ![]() at
at ![]() is,
is,
![]()
The right hand limit of ![]() at
at ![]() is,
is,
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]()
From the above observations, it can be concluded that ![]() is
is
continuous at all points of the real line.
Thus, ![]() has no point of discontinuity.
has no point of discontinuity.
Question 24: Determine if ![]() defined by
defined by ![]() , if
, if ![]() is a continuous function?
is a continuous function?
Solution: ![]()
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line.
be a point on the real line.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then
, then ![]()
![]()
It is known that, ![]()
![]()
![]()
![]()
![]()
![]()
Similarly,
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
From the above observations, it can be concluded that ![]() is continuous at every point of the real line.
is continuous at every point of the real line.
Thus, ![]() is a continuous function.
is a continuous function.
Question 25: Examine the continuity of ![]() , where
, where ![]() is defined by
is defined by ![]()
Solution: The given function is
![]()
The given function ![]() is defined at all the points of the real line.
is defined at all the points of the real line.
Let ![]() be a point on the real line.
be a point on the real line.
Case I:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II:If ![]() , then
, then ![]()
![]()
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
From the above observations, it can be concluded that ![]() is continuous at every point of the real line.
is continuous at every point of the real line.
Thus, ![]() is a continuous function.
is a continuous function.
Question 26: Find the values of ![]() so that the function
so that the function ![]() is continuous at the indicated point
is continuous at the indicated point ![]() at
at ![]()
Solution: The given function is
![]()
The given function ![]() is continuous at
is continuous at ![]() , if
, if ![]() is defined at
is defined at ![]() and if the value of the
and if the value of the ![]() at
at ![]() equals the limit of
equals the limit of ![]() at
at ![]() .
.
It is evident that ![]() is defined at
is defined at ![]() and
and ![]()
![]()
Put ![]()
Then ![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the value of ![]() .
.
Question 27: Find the values of ![]() so that the function
so that the function ![]() is continuous at the indicated point.
is continuous at the indicated point. ![]() at
at ![]()
Solution: The given function is ![]()
The given function ![]() is continuous at
is continuous at ![]() , if
, if ![]() is defined at
is defined at ![]() and if the value of the
and if the value of the ![]() at
at ![]() equals the limit of
equals the limit of ![]() at
at ![]() .
.
It is evident that ![]() is defined at
is defined at ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the value of ![]() .
.
Question 28: Find the values of ![]() so that the function
so that the function ![]() is continuous at the indicated point
is continuous at the indicated point ![]() at
at ![]()
Solution: The given function is ![]()
The given function ![]() is continuous at
is continuous at ![]() , if
, if ![]() is defined at
is defined at ![]() and if the value of the
and if the value of the ![]() at
at ![]() equals the limit of
equals the limit of ![]() at
at ![]() .
.
It is evident that ![]() is defined at
is defined at ![]() and
and ![]()
![]()
![]() .
.
![]()
![]()
![]()
Therefore, the value of ![]() .
.
Question 29: Find the values of ![]() so that the function
so that the function ![]() is continuous at the indicated point
is continuous at the indicated point ![]() at
at ![]() .
.
Solution: The given function is 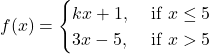
The given function ![]() is continuous at
is continuous at ![]() , if
, if ![]() is defined at
is defined at ![]() and if the value of the
and if the value of the ![]() at
at ![]() equals the limit of
equals the limit of ![]() at
at ![]() .
.
It is evident that ![]() is defined at
is defined at ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the value of ![]() .
.
Question 30:Find the values of ![]() such that the function defined by
such that the function defined by

is a continuous function.
Solution: 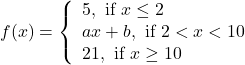
The given function is It is evident that ![]() is defined at all points of the real line.
is defined at all points of the real line.
If ![]() is a continuous function, then
is a continuous function, then ![]() is continuous at all real numbers.
is continuous at all real numbers.
In particular, ![]() is continuous at
is continuous at ![]() and
and ![]()
Since ![]() is continuous at
is continuous at ![]() , we obtain
, we obtain
![]()
![]()
![]()
![]()
Since ![]() is continuous at
is continuous at ![]() , we obtain
, we obtain
![]()
![]()
![]()
![]()
On subtracting equation (1) from equation ![]() , we obtain
, we obtain
![]()
![]()
By putting ![]() in equation (1), we obtain
in equation (1), we obtain
![]()
![]()
![]()
Therefore, the values of ![]() and
and ![]() for which
for which ![]() is a continuous function are 2 and 1 respectively.
is a continuous function are 2 and 1 respectively.
Question 31: Show that the function defined by ![]() is a continuous function.
is a continuous function.
Solution: The given function is ![]() .
.
This function ![]() is defined for every real number and
is defined for every real number and ![]() can be written as the composition of two functions as,
can be written as the composition of two functions as,
![]() , where
, where ![]() and
and ![]()
![]()
It has to be proved first that ![]() and
and ![]() are continuous functions.
are continuous functions.
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number.
be a real number.
Let ![]() . Put
. Put ![]()
If ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, ![]() is a continuous function.
is a continuous function.
Let ![]()
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number, then
be a real number, then ![]()
![]()
![]()
Therefore, ![]() is a continuous function.
is a continuous function.
It is known that for real valued functions ![]() and
and ![]() , such that
, such that ![]() is defined at
is defined at ![]() , if
, if ![]() is continuous at
is continuous at ![]() and if
and if ![]() is continuous at
is continuous at ![]() , then
, then ![]() is continuous at
is continuous at ![]() .
.
Therefore, ![]() is a continuous function.
is a continuous function.
Question 32: Show that the function defined by ![]() is a continuous function.
is a continuous function.
Solution: The given function is ![]() .
.
This function ![]() is defined for every real number and
is defined for every real number and ![]() can be written as the composition of two functions as,
can be written as the composition of two functions as,
![]() , where
, where ![]() and
and ![]()
![]()
It has to be proved first that ![]() and
and ![]() are continuous functions.
are continuous functions.
![]()
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number.
be a real number.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
![]() .
.
Therefore, ![]() is continuous at all
is continuous at all ![]() .
.
From the above three observations, it can be concluded that ![]() is continuous at all points.
is continuous at all points.
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number. Put
be a real number. Put ![]()
If ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, ![]() is a continuous function.
is a continuous function.
It is known that for real valued functions ![]() and
and ![]() , such that
, such that ![]() is defined at
is defined at ![]() , if
, if ![]() is continuous at
is continuous at
![]() and if
and if ![]() is continuous at
is continuous at ![]() , then
, then ![]() is continuous at
is continuous at ![]() .
.
Therefore, ![]() is a continuous function.
is a continuous function.
Question 33: Show that the function defined by ![]() is a continuous function.
is a continuous function.
Solution: The given function is ![]() .
.
This function ![]() is defined for every real number and
is defined for every real number and ![]() can be written as the composition of two functions as,
can be written as the composition of two functions as,
![]() , where
, where ![]() and
and ![]()
![]()
It has to be proved first that ![]() and
and ![]() are continuous functions.
are continuous functions.
![]() can be written as
can be written as ![]()
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number.
be a real number.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
![]()
Therefore, ![]() is continuous at all
is continuous at all ![]() .
.
From the above three observations, it can be concluded that ![]() is continuous at all points.
is continuous at all points.
Let ![]()
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number. Put
be a real number. Put ![]()
If ![]() , then
, then ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, ![]() is a continuous function.
is a continuous function.
It is known that for real valued functions ![]() and
and ![]() , such that
, such that ![]() is defined at
is defined at ![]() , if
, if ![]() is continuous at
is continuous at ![]() and if
and if ![]() is continuous at
is continuous at ![]() , then
, then ![]() is continuous at
is continuous at ![]() .
.
Therefore, ![]() is a continuous function.
is a continuous function.
Question 34: Find all the points of discontinuity of ![]() defined by
defined by ![]() .
.
Solution: The given function is ![]() .
.
The two functions, ![]() and
and ![]() are defined as
are defined as ![]() and
and ![]() .
.
Then, ![]()
The continuity of ![]() and
and ![]() are examined first.
are examined first.
![]() can be written as
can be written as ![]()
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number.
be a real number.
Case I: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II: If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
![]()
Therefore, ![]() is continuous at all
is continuous at all ![]() .
.
From the above three observations, it can be concluded that ![]() is continuous at all points.
is continuous at all points.
![]()
It is evident that ![]() is defined for every real number.
is defined for every real number.
Let ![]() be a real number.
be a real number.
Case I:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case II:If ![]() , then
, then ![]()
![]()
![]()
Therefore, ![]() is continuous at all points
is continuous at all points ![]() , such that
, such that ![]() .
.
Case III: If ![]() , then
, then ![]()
![]()
![]()
![]()
Therefore, ![]() is continuous at
is continuous at ![]() .
.
From the above three observations, it can be concluded that ![]() is continuous at all points. It concludes that
is continuous at all points. It concludes that ![]()
and ![]() are continuous functions. Therefore,
are continuous functions. Therefore, ![]() is also a continuous function.
is also a continuous function.
Therefore, ![]() has no point of discontinuity.
has no point of discontinuity.