Case study application of derivative 4 chapter 6 class 12

Case study Chapter 6 (Application of derivative)

Case study 4:- Read the following and answer the question:(Case study application of derivative 4 )

These days chinese and Indian troops are engaged in aggressive melee,face-off skirmishes at location near the disputed Pangong Lake in Ladakh.

One day a helicopterof enemy is flying along the curve represented by y = x² + 7. A soldier placed at (3, 7) wants to shoot down the helicopter when it is nearest to him.

(i) If $(x_1, y_1)$ represents the position of helicopter on the curve y = x² +7, when the distance D from soldier placed at S(3, 7) is minimum, then the relation between $x_1,y_1$ is

(a) $x_1 = y_1^2 + 7$ (b) $y_1 = x_1^2 + 7$

(ii) The distance ‘D’ expressed as a function of $x_1$ is

(a) $D=x_1^2-6x_1 + x_1^4$ (b) $D = x_1^2-6x_1+9+x_1^4$

(iii) The soldier at S wants to know when the enemy helicopter is nesrest to soldier, then the value $y_1$ should be

(a) 4 (b) 3

(iv) When the enemy helicopter is nearest to soldier, then the value of D should be

(a) 4 units (b) 5 units

(v) The narest position of helicopter from soldier is

(a) (1, √3) (b) (1, 8)

Solution:(i) Answer (a)

Since, $(x_1, y_1)$ lie on the curve y = x² + 7

⇒ $(x_1, y_1)$ satisfy the equation of curve

⇒ $y_1 = x_1^2 + 7$

(ii) Answer (c)

Here, since soldier is at (3, 7).

$D = \sqrt{(x_1-3)^2+(y_1-7)^2}$

$\Rightarrow D^2 = (x_1-3)^2+(y_1-7)^2$

Since, $(x_1, y_1)$ lie on the curve y =x² + 7

⇒ $y_1 = x_1^2+7$

$\therefore D^2 = (x_1-3)^2+(y_1+7-7)^2$

$D^2 = x_1^2-6x_1+9+x_1^4$

(iii) Answer (c)

We have ,

$D^2 = x_1^2-6x_1+9+x_1^4$

∴ $\frac{dD^2}{dx_1} = 2x_1-6+4x_1^3$

For minimum value of D i.e. D²

$\frac{dD^2}{dx_1} = 0 \Rightarrow 2x_1+4x_1^3-6=0$

$4x_1^2(x_1-1)+4x_1(x_1-1)+6(x_1-1)=0$

$\Rightarrow (x_1-1)(4x_1^2+4x_1+6)=0$

$\Rightarrow x_1-1=0$

[Since $4x_1^2+4x_1+6=0$ have no real roots i.e.real value of $x_1$ is not possible.]

$\Rightarrow x_1 = 1$

⇒ For minimum points,(distance) or nearest distance $x_1 = 1$

Also

$\frac{d^2D^2}{dx_1^2}= 2+12x_1^2$

$\Rightarrow \frac{d^2D^2}{dx_1^2} = +(ve)$

Since, $(x_1, y_1)$ lie on the curve y = x² + 7

⇒ $y_1 = x_1^2 + 7$

$\Rightarrow y_1 = 1^2 + 7= 1+7 = 8$

(iv)Answer (c)

For nearest distance D i.e. minimum value of D, $x_1 = 1$

Since, $D^2 = x_1^2-6x_1+9+x_1^4$

$\Rightarrow = 1^2- 6(1)+9+(1)^4$

$\Rightarrow D^2 =1-6+9+1$

$\Rightarrow D^2 =5$

$\Rightarrow D = \sqrt{5}$

(v) Answer (b)

For minimum value of D

$x_1 = 1$ and $y_1 = 8$

∴ Nearest position of helicopter is (1, 8).

Some other Case study problem

Case study 1: Read the following and answer the question(Case study application of derivative 1 )
A recangular hall is to be developed for a meeting of farmers in an agriculture college to aware them for new technique in cultivation. It is given that the floor has a fixed perimeter P as shown below.

Solution: For solution click here

Case study 2:- Read the following and answer the question.(Case study application of derivative 2)

Dr. Ritam residing to Delhi went to see an apartment of 3 BHK in Noida. The window of the house was in the form of a rectangle surmounted by a semicircular opening having a perimeter of the window 10 m as shown in figure.

Solution: For solution click here

Case study 3:- Read the following and answer the question:(Case study application of derivative 3)

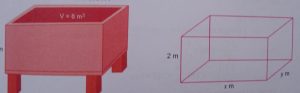
On the request of villagers, a construction agency designs a tank with the help of an architect. Tank consist of rectangular base with recangular sides, open at the top so that its depth is 2 m and volume is 8 cubic meter as shown below:

Solution: For solution click here

Case study 5:– Indian Railways is the largest rail network in Asia and world’s second largest. No doubt huge amount of money of Indian government paid as fuel cost. Decreasing fuel cost can increase railway profit and hence will improve Indian economy.(Case study application of derivative 5 )

Case study application of derivative 5 — Indian Railways is the largest rail network in Asia and world’s second largest. No doubt

This is the fact that the fuel cost for running a train is proportional to the square of the speed generated in km per hour. The fuel cost is ₹ 48 per hour at speed 16 km per hour and fixed charges amount to ₹ 1200 per hour.

Solution: For solution click here

Case study application of integral 4 — A boy design a pizza by cutting it with a knife on a card board.

Case study linear programming 4 — A share is refferred to as a unit of owner ship which represents an equal proportion of a

Case study problem probability 6 chapter 13 class 12 — A coach is training 3 players. He observes that the player A can hit a target 4

Some other Case study problem

Leave a Comment Cancel reply