EXERCISE 3.1 (MATRIX)
Class 12 ncert solution math exercise 3.1 matrix
Question 1: (i) The order of the matrix
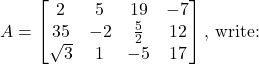
(ii) The number of elements
(iii) Write the elements ![]()
Solution: (i) Since, in the given matrix, the number of rows is 3 and the number of columns is 4 , the order of the matrix is ![]() .
.
(ii) Since the order of the matrix is ![]() , there are
, there are ![]() elements.
elements.
(iii) Here,
![]()
![]()
![]()
![]()
![]()
Question 2: If a matrix has 24 elements, what are the possible order it can have? What, if it has 13 elements?
Solution: We know that if a matrix is of the order ![]() , it has
, it has ![]() elements. Thus, to find all the possible orders of a matrix having 24 elements, we have to find all the ordered pairs of natural numbers whose product is 24 .
elements. Thus, to find all the possible orders of a matrix having 24 elements, we have to find all the ordered pairs of natural numbers whose product is 24 .
The ordered pairs are: ![]() and
and ![]() .
.
Hence, the possible orders of a matrix having 24 elements are:
![]()
![]() and
and ![]() are the ordered pairs of natural numbers whose product is 13 . Hence, the possible orders of a matrix having 13 elements are
are the ordered pairs of natural numbers whose product is 13 . Hence, the possible orders of a matrix having 13 elements are ![]() and
and ![]() .
.
Question 3: If a matrix has 18 elements, what are the possible order it can have? What, if it has 5 elements?
Solution: We know that if a matrix is of the order ![]() , it has
, it has ![]() elements. Thus, to find all the possible orders of a matrix having 18 elements, we have to find all the ordered pairs of natural numbers whose product is 18 .
elements. Thus, to find all the possible orders of a matrix having 18 elements, we have to find all the ordered pairs of natural numbers whose product is 18 .
The ordered pairs are: ![]() and
and ![]() .
.
Hence, the possible orders of a matrix having 18 elements are:
![]()
![]() and
and ![]() are the ordered pairs of natural numbers whose product is 5 .
are the ordered pairs of natural numbers whose product is 5 .
Hence, the possible orders of a matrix having 5 elements are ![]() and
and ![]() .
.
Question 4: Construct a ![]() matrix,
matrix, ![]() , whose elements are given by:
, whose elements are given by:
(i) ![]()
(ii) ![]()
(iii) ![]()
Solution: In general, a ![]() matrix is given by
matrix is given by ![]()
(i) ![]()
Therefore,
![]()
![]()
![]()
![]()
![]()
(ii) ![]()
Therefore,
![]()
![]()
![]()
![]()
Thus, the required matrix is ![]()
(iii) ![]()
Therefore,
![]()
![]()
![]()
![]()
Thus, the required matrix is ![]()
Question 5: In general, a ![]() matrix whose elements are given by
matrix whose elements are given by
(i) ![]()
(ii) ![]()
Solution: 
(i) Given ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thus, the required matrix is
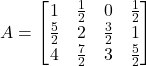
(ii) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thus, the required matrix is 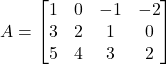
Question 6: Find the value of ![]() and
and ![]() from the following equation:
from the following equation:
(i) ![]()
(ii) ![]()
(iii) 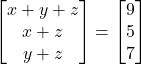
Solution: (i) ![]()
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
![]()
(ii) ![]()
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
![]()
![]()
![]()
Hence,
![]()
![]()
We know that ![]()
![]()
![]()
![]()
![]()
Equating ![]() and
and ![]() , we get
, we get ![]()
Similarly, Equating ![]() and
and ![]() , we get
, we get ![]()
Thus, ![]() or
or ![]()
(iii) 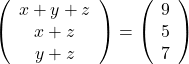
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
![]()
![]()
![]()
From (1) and (2), we have
![]()
![]()
From (3), we have
![]()
![]()
Therefore,
![]()
![]()
![]()
Thus, ![]()
Question 7: Find the value of ![]() and
and ![]() from the equation:
from the equation:
![]()
Solution: ![]()
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get:
![]()
![]()
![]()
![]()
From (2),
![]()
Putting this value in (1),
Hence,
![]()
![]()
![]()
Putting
![]() in (3),
in (3),
![]()
![]()
Putting ![]() in
in ![]() ,
,
![]()
![]()
Thus, ![]() and
and ![]() .
.
Question 8: ![]() is a square matrix, if
is a square matrix, if
(A) ![]()
(B) ![]()
(C) ![]()
(D) None of these
Solution: It is known that a given matrix is said to be a square matrix if the number of rows is equal to the number of columns.
Therefore, ![]() is a square matrix, if
is a square matrix, if ![]() .
.
Thus, the correct option is {C}.
Question 9: Which of the given values of ![]() and
and ![]() make the following pair of matrices equal
make the following pair of matrices equal
![]()
(A) ![]()
(B) Not possible to find
(C) ![]()
(D) ![]()
Solution: The given matrices are ![]() and
and ![]()
Equating the corresponding elements, we get:
![]()
![]()
![]()
![]()
We find that on comparing the corresponding elements of the two matrices, we get two different values of ![]() , which is not possible.
, which is not possible.
Hence, it is not possible to find the values of ![]() and
and ![]() for which the given matrices are equal.
for which the given matrices are equal.
Thus, the correct option is ![]() .
.
Question 10: The number of all possible matrices of order ![]() with each entry 0 or 1 is:
with each entry 0 or 1 is:
(A) 27
(B) 18
(C) 81
(D) 512
Solution: The given matrix of the order ![]() has 9 elements and each of these elements can be either 0 or 1 .
has 9 elements and each of these elements can be either 0 or 1 .
Now, each of the 9 elements can be filled in two possible ways.
Hence, by the multiplication principle, the required number of possible matrices is ![]() .
.
Thus, the correct option is D.