EXERCISE 6.5( Application of derivative)

Question 1: Find the maximum and minimum values, if any, of the following functions given by:(class 12 maths ex 6.5 ncert solution)

(i) $f(x)=(2 x-1)^2+3$

(ii) $f(x)=9 x^2+12 x+2$

(iii) $f(x)=-(x-1)^2+10$

(iv) $g(x)=x^3+1$

Solution: (i) Given function is:

$f(x)=(2 x-1)^2+3$

We know that

$(2 x-1)^2 \geq 0$ for all $x \in \mathbf{R}$

Adding 3 both sides, we get

$(2 x-1)^2+3 \geq 0+3$

$f(x) \geq 3$

The minimum value of $f(x)$ is 3

when $2 x-1=0$ ,

$x=\frac{1}{2}$

this function does not have a maximum value.

(ii) Given function is:

$f(x)=9 x^2+12 x+2$

$f(x)=9\left(x^2+\frac{4 x}{3}+\frac{2}{9}\right)$

$f(x)=9\left[x^2+\frac{4 x}{3}+\left(\frac{2}{3}\right)^2-\left(\frac{2}{3}\right)^2+\frac{2}{9}\right]$

$=9\left[\left(x+\frac{2}{3}\right)^2-\frac{4}{9}+\frac{2}{9}\right]$

$f(x)=9\left(x+\frac{2}{3}\right)^2-2$

As $9\left(x+\frac{2}{3}\right)^2 \geq 0 \text { for all } \mathrm{x} \in \mathrm{R}$

Subtracting 2 from both sides,

$9\left(x+\frac{2}{3}\right)^2-2 \geq 0-2$

$f(x) \geq-2$

Therefore, minimum value of $f(x)$ is $-2$ and is obtained when

$x+\frac{2}{3}=0 \text {, that is, } x=\frac{-2}{3}$

And this function does not have a maximum value.

(iii) Given function is:

$f(x)=-(x-1)^2+10$

As $(x-1)^2 \geq 0$ for all $x \in \mathbf{R}$

Multiplying both sides by $-1$ and adding 10 both sides,

$-(x-1)^2+10 \leq 10$

$f(x) \leq 10 \text { [Using equation (1)] }$

Maximum value of $f(x)$ is 10 which is obtained when

$x-1=0\Rightarrow x=1$ .

And minimum value of $f(x)$ does not exist.

(iv) Given function is: $g(x)=x^3+1$

At $x \rightarrow \infty \quad g(x) \rightarrow \infty$

At $x \rightarrow-\infty \quad g(x) \rightarrow-\infty$

Hence, maximum value and minimum value of $g(x)$ do not exist.

Question :2) Find the maximum and minimum values, if any, of the following functions given by:

(i) $f(x)=|x+2|-1$

(ii) $g(x)=|x+1|+3$

(iii) $h(x)=\sin (2 x)+5$

(iv) $f(x)=|\sin 4 x+3|$

(v) $h(x)=x+1, x \in(-1,1)$

Solution: (i) Given function is: $f(x)=|x+2|-1$

We know that

$|x+2| \geq 0$ for all $x \in \mathrm{R}$

Subtracting 1 from both sides,

$|x+2|-1 \geq-1$

$f(x) \geq-1$

Therefore, minimum value of $f(x)$ is $-1$

when $x+2=0\Rightarrow x=-2$ .
.
From equation (1), maximum value of $f(x) \rightarrow \infty$ hence it does not exist.

(ii) Given function is: $g(x)=-|x+1|+3$

We know that

$|x+1| \geq 0$ for all $x \in \mathbf{R}$

Multiplying by $-1$ both sides and adding 3 both sides,

$-|x+1|+3 \leq 3$

$g(x) \leq 3$

Maximum value of $g(x)$ is 3

when $x+1=0 \Rightarrow x=-1$ .

From equation (1), minimum value of $g(x) \rightarrow-\infty$ , does not exist.

(iii) Given function is: $h(x)=\sin (2 x)+5$

We know that

$-1 \leq \sin 2 x \leq 1$ for all $x \in \mathbf{R}$

Adding 5 to all sides,

$-1+5 \leq \sin 2 x+5 \leq 1+5$

$4 \leq h(x) \leq 6$

Therefore, minimum value of $h(x)$ is 4 and maximum value is 6 .

(iv) Given function is: $f(x)=|\sin 4 x+3|$

We know that

$-1 \leq \sin 4 x \leq 1$ for all $x \in \mathbf{R}$

Adding 3 to all sides,

$-1+3 \leq \sin 2 x+5 \leq 1+3$

$2 \leq f(x) \leq 4$

Therefore, minimum value of $f(x)$ is 2 and maximum value is 4 .

(v) Given function is:

$h(x)=x+1, x \in(-1,1)$

As $-1<x<1$

Adding 1 to both sides,

$-1+1<x+1<1+1$

$0<h(x)<2$

Therefore, neither minimum value not maximum value of $h(x)$ exists.

Question: 3) Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:

(i) $f(x)=x^2$

(ii) $g(x)=x^3-3 x$

(iii) $h(x)=\sin x+\cos x, 0<x<\frac{\pi}{2}$

(iv) $h(x)=\sin x-\cos x, 0<x<2\pi$

(v) $f(x)=x^3-6 x^2+9 x+15$

(vi) $g(x) \frac{x}{2}+\frac{2}{x}, x>0$

(vii) $g(x)=\frac{1}{x^2+2}$

(viii) $f(x)=x \sqrt{1-x}, x>0$

Solution: (i) Given function is:

$f(x)=x^2$

$f'(x)=2 x$ and $f''(x)=2$

Now $f'(x)=0$

$x=0$ [Turning point]

Again, when $\mathrm{x}=0, f''(x)=2$ [Positive]

Therefore, $\mathrm{x}=0$ , is a point of local minima and
local minimum value $=f(0)=(0)^2=0$

(ii) Given function is:

$g(x)=x^3-3 x$

$g^{\prime}(x)=3 x^2-3$ and $g^{\prime \prime}(x)=6 x$

Now $g'(x)=0$

$3 x^2-3=0$

$3\left(x^2-1\right)=0$

$3(x+1)(x-1)=0$

$x=-1$ or $x=1$ [Turning points]

Again, when $x=-1$ ,

$g^{\prime \prime}(x)=6 x=6(-1)=-6$ [Negative]

$x=-1$ is a point of local maxima and local maximum value

$g(-1)=(-1)^3-3(-1)=2$

And

when $\mathrm{x}=1 ; g''(x)=6 x$

$g(1)=6(1)=6$ [Positive]

$x=1$ , is a point of local minima and local minimum value

$g(1)=(1)^3-3(1)=-2$

(iii) Given function is:

$h(x)=\sin x+\cos x\left(0<x<\frac{\pi}{2}\right)$

$h^{\prime}(x)=\cos x-\sin x \text { and } h^{\prime \prime}(x)=-\sin x-\cos x$

Now $h'(x)=0$

$\cos x-\sin x=0$

$-\sin x=-\cos x$

$\frac{\sin x}{\cos x}=1$

$\tan x=1 \text { [Positive] }$

$x$ can have values in both 1st and 3rd quadrant.

But, $\left(0<x<\frac{\pi}{2}\right)$

therefore, $x$ is only in I quadrant.

As, $\tan x=1=\frac{\pi}{4}$

$\text { At }{x=\frac{\pi}{4}}$

$h''(x)=-\sin x-\cos x$

$\Rightarrow h''(x)=-\sin \frac{\pi}{4}-\cos \frac{\pi}{4}$

$=\frac{-1}{\sqrt{2}}-\frac{1}{\sqrt{2}}$

$=\frac{-2}{\sqrt{2}}=-\sqrt{2} \text { [Negative] }$

$x=\frac{\pi}{4}$ is a point of local maxima and local maxima value

$= h\left(\frac{\pi}{4}\right)=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}$

$= \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$

(iv) Given function is: $f(x)=\sin x-\cos x(0<x<2 \pi)$

$f^{\prime}(x)=\cos x+\sin x$

and $f'(x)=-\sin x+\cos x$

Now $f^{\prime}(x)=0$

$\cos x+\sin x=0$

$\sin x=-\cos x$

$\frac{\sin x}{\cos x}=-1$

$\tan x=-1 \text { [Negative] }$

$x$ can have values in both 2 nd and 4 th quadrant.

$\tan x=-1=-\tan \frac{\pi}{4}$

$\Rightarrow x = \frac{3\pi}{4}$ , $\frac{7\pi}{4}$

$f''(x)=-\sin x+\cos x$

$\text { At } x=\frac{3 \pi}{4}$

$=-\sin \frac{3 \pi}{4}+\cos \frac{3 \pi}{4}$

$\Rightarrow f''(x)={-\sin \left(\pi-\frac{\pi}{4}\right)+\cos \left(\pi-\frac{\pi}{4}\right)}$

$=-\sin \frac{\pi}{4}-\cos \frac{\pi}{4}$

$=\frac{-1}{\sqrt{2}}-\frac{1}{\sqrt{2}}$

$=\frac{-2}{\sqrt{2}}=-\sqrt{2} \text { [Negative] }$

So, $x=\frac{3 \pi}{4}$ is a point of local maxima and local maximum value

$=\sin \left(\pi-\frac{\pi}{4}\right)-\cos \left(\pi-\frac{\pi}{4}\right)$

$=\sin ^{\frac{\pi}{4}}+\cos \frac{\pi}{4}$

$=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$

$\text { At }{x=\frac{7 \pi}{4}} ,f^{\prime \prime}(x)=-\sin x+\cos x$

$=-\sin \frac{7 \pi}{4}+\cos \frac{7 \pi}{4}$

$\text { Which implies; } h^{\prime \prime}(x)=-\sin \left(2 \pi-\frac{\pi}{4}\right)+\cos \left(2 \pi-\frac{\pi}{4}\right)$

$=\sin ^{\frac{\pi}{4}}+\cos \frac{\pi}{4}$

$=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}$

$=\frac{2}{\sqrt{2}}=\sqrt{2} \text { [Positive] }$

$x=\frac{7 \pi}{4}$

is a point of local maxima and local maximum value

$f\left(\frac{7 \pi}{4}\right)=\sin \frac{7 \pi}{4}-\cos \frac{7 \pi}{4}$

$\sin \left(2 \pi-\frac{\pi}{4}\right)-\cos \left(2 \pi-\frac{\pi}{4}\right)$

$=-\sin \frac{\pi}{4}-\cos \frac{\pi}{4}$

$=\frac{-1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}$

(v) Given function is:

$f(x)=x^3-6 x^2+9 x+15$

$f'(x)=3 x^2-12 x+9$ and $f''(x)=6 x-12$

Now $f'(x)=0$ .

$3 x^2-12 x+9=0$

$\Rightarrow x^2-4 x+3=0$

$\Rightarrow (x-1)(x-3)=0$

$x=1 \text { or } x=3 \text { [Turning points] }$

$\text { At } x=1, f^{\prime \prime}(x)=6 x-12=6-12=-6 \text { [Negative] }$

$x=1$ is a point of local maxima and local maximum value is
$f(1)=(1)^3-6(1)^2+9(1)+15=19$

At $x=3, f^{\prime \prime}(x)=6 x-12=6 \times 3-12=6$ [Positive]

$x=3$ is a point of local minima and local minimum value is

$f(3)=(3)^3-6(3)^2+9(3)+15=15$

(vi) Given function is:

$g'(x)=\frac{1}{2}-\frac{2}{x^2}$

$=\frac{x^2-4}{2 x^2}$

$=\frac{(x+2)(x-2)}{2 x^2}$

and $g''(x)=\frac{4}{x^3}$

$\text { Now } g'(x)=0$

$\Rightarrow \frac{(x+2)(x-2)}{2 x^2}=0$

$(x+2)(x-2)=0$

$x=-2 \text { or } x=2$

But $x>0$ , therefore $x=2$ is only the turning point.

$x=2$ is a point of local minima and local minimum value is

$g(2)=\frac{2}{2}+\frac{2}{2}=2$

(vii) Given function is:

$h(x)=\frac{1}{x^2+2}=\left(x^2+2\right)^{-1}$

$h'(x)=(-1)\left(x^2+2\right)^{-2}(2 x)$

$=\frac{-2 x}{\left(x^2+2\right)^2}$

and

$h^{\prime \prime}(x)=\left[\frac{\left(x^2+2\right)^2 \cdot 2-2 x \cdot 2\left(x^2+2\right) 2 x}{\left(x^2+2\right)^4}\right]$

$=\frac{-2\left(2-3 x^2\right)}{\left(x^2+2\right)^3}$

Now $h'(x)=0$

$\frac{-2 x}{\left(x^2+2\right)^2}=0$

$\Rightarrow x=0$

$\text { At } x=0, h''(x)=\frac{-2\left(2-3 x^2\right)}{\left(x^2+2\right)^3}$

$=\frac{-2(2-0)}{(0+2)^3}=\frac{-4}{8}=\frac{-1}{2}$ [Negative]

$\mathrm{x}=0$ is a point of local maxima and local maximum value is

$h(0)=\frac{1}{0+2}=\frac{1}{2}$

(viii) Given function is: $f(x)=x \sqrt{1-x}, x \leq 1$

$f^{\prime}(x)=x \cdot \frac{1}{2}(1-x)^{\frac{-1}{2}} \frac{d}{d x}(1-x)+\sqrt{1-x} \cdot 1$

$= \frac{-x}{2 \sqrt{1-x}}+\sqrt{1-x}$

$= \frac{-x+2(1-x)}{2 \sqrt{1-x}}=\frac{2-3 x}{2 \sqrt{1-x}}$

And

$f^{\prime \prime}(x)=\frac{1}{2} \cdot \frac{\sqrt{1-x} \cdot(-3)-(2-3 x) \cdot \frac{1}{2 \sqrt{1-x}}(-1)}{1-x}$

$\frac{-6(1-x)+2-3 x}{4(1-x)^{\frac{3}{2}}}$

$= \frac{3 x-4}{4(1-x)^{\frac{3}{2}}}$

$= \frac{(1-2)}{4}$

Now $f^{\prime}(x)=0$

$\frac{2-3 x}{2 \sqrt{1-x}}=0$

$2-3 x=0$

$x=\frac{2}{3}$

$x=\frac{2}{3}$ is a point of local maxima and local maximum value is

$f\left(\frac{2}{3}\right)=x \sqrt{1-x}$

$=\frac{2}{3} \sqrt{1-\frac{2}{3}}=\frac{2 \sqrt{3}}{9}$

$f''\left(\frac{2}{3}\right)=\frac{3\left(\frac{2}{3}\right)-4}{4\left(1-\frac{2}{3}\right)^{\frac{3}{2}}}$

Again

$\frac{2-4}{4\left(\frac{1}{3}\right)^{\frac{3}{2}}}=\frac{-1}{2\left(\frac{1}{3}\right)^{\frac{3}{2}}}<0$

Therefore, $\mathrm{f}(\mathrm{x})$ has local maximum value at $x=\frac{2}{3}$ .

Question:4) Prove that the following functions do not have maxima or minima:

(i) $f(x)=e^x$

(ii) $g(x)=\log x$

(iii) $h(x)=x^3+x^2+x+1$

Solution: (i) Given function is: $f(x)=e^x$

$f'(x)=e^x$

Now $f'(x)=0$

$e^x=0$

But this gives no real value of $x$ . Therefore, there is no turning point. $f(x)$ does not have maxima or minima.

(ii) Given function is: $g(x)=\log x$

$g'(x)=\frac{1}{x}$

$\text { Now } g'(x)=0$

$\frac{1}{x}=0$

$1=0 \text { (which is not possible) }$

$f(x) \text { does not have maxima or minima. }$

(iii) Given function is: $h(x)=x^3+x^2+x+1$

$h^{\prime}(x)=3 x^2+2 x+1$

$\text { Now }h'(x)=0$

$3 x^2+2 x+1=0$

$\Rightarrow x=\frac{-2 \pm \sqrt{4-12}}{6}$

$=\frac{-2 \pm \sqrt{-8}}{6}$

$=\frac{-1 \pm \sqrt{2} i}{3}$

Here, values of $x$ are imaginary.

$h(x)$ does not have maxima or minima.

Question:5) Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:

(i) $f(x)=x^3, x \in[-2,2]$

(ii) $f(x)=\sin x+\cos x, x \in[0, \pi]$

(iii) $f(x)=4 x-\frac{1}{2} x^2, x \in\left[-2, \frac{9}{2}\right]$

(iv) $f(x)=(x-1)^2+3, x \in[-3,1]$

Solution: (i) Given function is: $f(x)=x^3, x \in[-2,2]$

$f^{\prime}(x)=3 x^2$

Now $f'(x)=0$

$3 x^2=0$

$x=0 \in[-2,2]$

$\text { At } x=0, f(0)=0$

$\text { At }x=-2$ ,

$f(-2)=(-2)^3=-8$

$\text { At }x =2, f(2)=(2)^3=8$

Therefore, absolute minimum value of $f(x)$ is $-8$ and absolute maximum value is 8 .

(ii) Given function is: $f(x)=\sin x+\cos x, x \in[0, \pi]$

$f'(x)=\cos x-\sin x$

Now $f'(x)=0$

$\cos x-\sin x=0$

$\Rightarrow -\sin x=-\cos x$

$\tan x=1 \text { [Positive] }$

$\mathrm{x}$ lies in I quadrant.

$\tan x=1=\tan \frac{\pi}{4}$

$x=\frac{\pi}{4}$

$f\left(\frac{\pi}{4}\right)=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}$

$=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$

$f(0)=\sin 0+\cos 0=0+1=1$

$f(\pi)=\sin \pi+\cos \pi=0-1=-1$

Therefore, absolute minimum value is $-1$ and absolute maximum value is 1 .

(iii) Given function is:

$f(x)=4 x-\frac{1}{2} x^2, x \in\left(-2, \frac{9}{2}\right)$

$f'(x)=4-\frac{1}{2}(2 x)=4-x$

Now $f'(x)=0$

$4-x=0$

$x=4 \in\left(-2, \frac{9}{2}\right)$

$\text { At } x=4, \quad f(4)=16-\frac{1}{2}(16)=16-8=8$

$\text { At } x=-2, \quad f(-2)=4(-2)-\frac{1}{2}(4)=-8-2=-10$

$\text { At } x=\frac{9}{2}, f\left(\frac{9}{2}\right)=4\left(\frac{9}{2}\right)-\frac{1}{2}\left(\frac{9}{2}\right)^2$

$=18-\frac{81}{8}=\frac{63}{8}$

Therefore, absolute minimum value is $-10$ and absolute maximum value is 8 .

(iv) Given function is:

$f'(x)=2(x-1)$

Now $f'(x)=0$

$2(x-1)=0$

$x=1 \in(-3,1)$

$\text { At } x=1, f(1)=(1-1)^2+3=3$

$\text { At } x=-3, f(-3)=(-3-1)^2+3$

$=16+3=19$

Therefore, absolute minimum value is 3 and absolute maximum value is 19 .

Question:6) Find the maximum profit that a company can make, if the profit function is given by $p(x)=41+24 x-18 x^2$ .

Solution: Profit function $p(x)=41+24 x-18 x^2$

$p'(x)=24-36 x \text { and } p''(x)=-36$

Now $p^{\prime}(x)=0$

$24-36 x=0$

$x=\frac{24}{36}=\frac{2}{3}$

$\text { At } x=\frac{2}{3}, p^{\prime \prime}(x)=-36 \text { [Negative] }$

$p(x)$ has a local maximum value at $x=\frac{2}{3}$ .

$\text { At }{x=\frac{2}{3}} \text {, Maximum profit }$

$=41+24\left(\frac{2}{3}\right)-18\left(\frac{4}{9}\right)$

$=41+16-8=49$

Question:7) Find both the maximum value and minimum value of $3 x^4-8 x^3+12 x^2-48 x+25$ on the interval $[\mathbf{0}, \mathbf{3}]$ .

Solution: $f(x)=3 x^4-8 x^3+12 x^2-48 x+25$ on [0, 3]

$f'(x)=12 x^3-24 x^2+24 x-48$

Now $f^{\prime}(x)=0$

$12 x^3-24 x^2+24 x-48=0$

$\Rightarrow x^3-2 x^2+2 x-4=0$

$(x-2)\left(x^2+2\right)=0$

$x=2 \text { or } x=\pm \sqrt{2}$

As $x=\pm \sqrt{2}$ is imaginary, therefore it is rejected.

here $x=2$ is turning point.

$\text { At } x=2, f(2)=3(16)-8(8)+12(4)-48(2)+25=-39$

$\text { At } x=0 \quad f(0)=25$

$\text { At } x=3, f(3)=3(81)-8(27)+12(9)-48(3)+25=16$

Therefore, absolute minimum value is $-39$ and absolute maximum value is 25 .

Question:8) At what points on the interval ${[0,2 \pi]}$ does the function $\sin 2 x$ attain its maximum value?

Solution: Consider $f(x)=\sin 2 x$

$f^{\prime}(x)=2 \cos 2 x$

Now $f^{\prime}(x)=0$

$2 \cos 2 x=0$

$2 x=(2 n+1) \frac{\pi}{2}$

$x=(2 n+1) \frac{\pi}{4}$

$\text { Put }{n=0,1,2,3 ;}$

$x=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4} \in[0,2 \pi]$

$\text { Now } f(x)=\sin 2 x$

$f\left[(2 n+1) \frac{\pi}{4}\right]=\sin (2 n+1) \frac{\pi}{2}$

$=(-1)^n\sin{\frac{\pi}{2}}$

$=(-1)^n$

$\text { Putting } n=0,1,2,3 ;$

$f\left(\frac{\pi}{4}\right)=(-1)^0=1$

$f\left(\frac{7 \pi}{4}\right)=(-1)^3=-1$

$f\left(\frac{3 \pi}{4}\right)=(-1)^1=-1$

$f\left(\frac{5 \pi}{4}\right)=(-1)^2=1$

$\text { Also } f(0)=\sin 0=0$

and $f(2 \pi)=\sin 4 \pi=0$

$\text { As } f(x) \text { attains its maximum value } 1 \text { at } x=\frac{\pi}{4} \text { and } x=\frac{5 \pi}{4} .$

Therefore, the required points are $\left(\frac{\pi}{4}, 1\right)$ and $\left(\frac{5 \pi}{4}, 1\right)$ .

Question:9 What is the maximum value of the function $\sin x+\cos x$ ?

Solution: Consider $f(x)=\sin x+\cos x$

$f'(x)=\cos x-\sin x$ —(i)

Now $f'(x)=0$

$\cos x-\sin x=0$

$-\sin x=-\cos x$

$\tan x = 1$

$\Rightarrow x = \frac{\pi}{4}, \frac{5\pi}{4}$

Again differentiate with respect to x of (i)

$f''(x) = -\sin x -\cos x$

(i) At $x = \frac{\pi}{4}$

$f''(\frac{\pi}{4}) = -\sin(\frac{\pi}{4})-\cos(\frac{\pi}{4})$

$\Rightarrow f''(\frac{\pi}{4}) = -\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}$

$\Rightarrow f''(\frac{\pi}{4}) = -\frac{2}{\sqrt{2}}<0$

f(x) is maximum at $x = \frac{\pi}{4}$ and maximum value
is

$f(\frac{\pi}{4}) = \sin(\frac{\pi}{4})+\cos(\frac{\pi}{4})$

$= \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}$

$= \frac{2}{\sqrt{2}}=\sqrt{2}$

(ii) At $x = \frac{5\pi}{4}$

$f''(\frac{5\pi}{4}) = -\sin(\frac{5\pi}{4})-\cos(\frac{5\pi}{4})$

$\Rightarrow f''(\frac{\pi}{4}) = \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}$

$\Rightarrow f''(\frac{\pi}{4}) = \frac{2}{\sqrt{2}}>0$

f(x) is minimum at $x = \frac{5\pi}{4}$ and minimum value
is

$f(\frac{\pi}{4}) = \sin(\frac{5\pi}{4})+\cos(\frac{5\pi}{4})$

$= -\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}$

$= -\frac{2}{\sqrt{2}}=-\sqrt{2}$

Therefore, maximum value of $f(x)$ is $\sqrt{2}$ and minimum value of $f(x)$ is $-\sqrt{2}$ .

Question:10) Find the maximum value of $2 x^3-24 x+107$ in the interval [1, 3]. Find the maximum value of the same function in $[-3,-1]$ .

Solution: Consider $f(x)=2 x^3-24 x+107$

$f'(x)=6 x^2-24$

Now $f^{\prime}(x)=0$

$6 x^2-24=0$

$x^2=4$

$x=\pm 2$

$x=2$ or $x=-2$ [Turning points]

For Interval $[1,3], x=2$ is turning point.

At $x=1, f(1)=2(1)-24(1)+107$

$=85$

At $x=2, \quad f(2)=2(8)-24(2)+107=75$

At $x=3, f(3)=2(27)-24(3)+107=89$

Therefore, maximum value of $f(x)$ is 89 .

For Interval $[-3,-1], x=-2$ is turning point.

$\text { At } x=-1, f(1)=2(-1)-24(-1)+107=129$

$\text { At } x=-2, \quad f(2)=2(-8)-24(-2)+107=139$

$\text { At } x=-3, \quad f(3)=2(-27)-24(-3)+107=125$

Therefore, maximum value of $f(x)$ is 139 .

Question:11) It is given that at $x=1$ , the function $x^4-62 x^2+a x+9$ attains its maximum value, on the interval $[\mathbf{0}, \mathbf{2 0}]$ . Find the value of $a$ .

Solution: Consider $f(x)=x^4-62 x^2+a x+9$

$f'(x)=4 x^3-124 x+$

As, $f(x)$ attains its maximum value at $x=1$ in the interval $[0,2]$ , therefore $f'(1)=0$

$f^{\prime}(1)=4-124+a=0$

$a-120=0$

$a=120$

Question:12) Find the maximum and minimum value of $x+\sin x$ on $[0,2 \pi]$ .

Solution: Consider $f(x)=x+\sin 2 x$

$f^{\prime}(x)=1+2 \cos 2 x$

$\text { Now } f^{\prime}(x)=0$

$1+2 \cos 2 x=0$

$2 \cos 2 x=-1$

$\cos 2 x=\frac{-1}{2}$

$2x = \frac{2\pi}{3},\frac{4\pi}{3},\frac{8\pi}{3},\frac{10\pi}{3},$

$\Rightarrow x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3},$

At $x = \frac{\pi}{3}$

$f(x)=\frac{\pi}{3}+\sin \frac{2\pi}{3}=\frac{\pi}{3}+\frac{\sqrt{3}}{2}$

At $x = \frac{2\pi}{3}$

$f(x)=\frac{2\pi}{3}+\sin \frac{4\pi}{3}=\frac{2\pi}{3}-\frac{\sqrt{3}}{2}$

At $x = \frac{4\pi}{3}$

$f(x)=\frac{4\pi}{3}+\sin \frac{8\pi}{3}=\frac{4\pi}{3}+\frac{\sqrt{3}}{2}$

At $x = \frac{5\pi}{3}$

$f(x)=\frac{5\pi}{3}+\sin \frac{10\pi}{3}=\frac{5\pi}{3}-\frac{\sqrt{3}}{2}$

At $f(0) = 0 +\sin 0= 0$

At $f(2\pi)= 2\pi + \sin4\pi = 2\pi$

Therfore max value $=2\pi$ and minimum value $= 0$

Question:13) Find two numbers whose sum is 24 and whose product is as large as possible.

Solution: Let two numbers be = x and y

$x+y=24$

Let Z is the product of two numbers

$Z=x.y$

$Z = x(24-x) ---(i)$

$\Rightarrow Z = 24x - x^2$

$\frac{dZ}{dx} = 24-2x$

And $\frac{d^2Z}{dx^2}= -2$

Now for max and minima $\frac{dZ}{dx}=0$

$24 - 2x=0\Rightarrow x = 12$

$\text { At } x=12, \frac{d^2 z}{d x^2}=-2 \text { [Negative] }$

$x=12$ is a point of local maxima

From equation (i), $y=24-12=12$

Therefore, the two required numbers are 12 and 12.

Question:14) Find two positive integers $x$ and $y$ such that $x+y=60$ and $x y^3$ is maximum.

Solution: Given function is: $x+y=60, x>0, y>0$

Let $\mathrm{Z}=x y^3$ [To be maximized]

Putting from equation (i), $x=60-y$ in equation (ii),

$\mathrm{Z}=(60-y) y^3=60 y^3-y^4$

$\frac{d \mathrm{Z}}{d y}=180 y^2-4 y^3=4 y^2(45-y)$

And $\frac{d^2Z}{dx^2}=360y-12y^2$

$\text { Now } \frac{d \mathrm{Z}}{d y}=0$

$4 y^2(45-y)=0$

$y=0,45$

At $y = 45$

$\frac{d^2Z}{dy^2} = 360(45)-12(45)^2$

$= 45(360-12\times 45)$

$= 45(360-540)= 45\times -180<0$

Therefore, $\mathrm{Z}$ is maximum when $y=45$ .
Hence, ${x y^3}$ is maximum when $x=60-45=15$ and $y=45$ .

Question:15) Find two positive integers $\mathrm{x}$ and $\mathrm{y}$ such that their sum is 35 and the product $x^2 y^5$ is a maximum.

Solution: Given function is: $x+y=35$

$y=35-x$

Let $z=x^2 y^5$

$z = x^2(35-x)^5 \quad[$ From equation (i) $]$

$\frac{d z}{d x}=x^2 \cdot 5(35-x)^4(-1)+(35-x)^5. 2 x$

$=x(35-x)^4[-5 x+(35-x) 2]$

$x(35-x)^4[-5 x+70-2 x]$

$=x(35-x)^4(70-7 x)$

$=7 x(35-x)^4(10-x)$

Now $\frac{d z}{d x}=0$

$7 x(35-x)^4(10-x)=0$

$x=0$ or $35-x=0$ or $10-x=0$

$x=0$ or $x=35$ or $x=10$

Now $x=0$ is rejected because according to question, $x$ is a positive number.

Also $x=35$ is rejected because from equation (i), $y=35-35=0$ , but $y$ is positive.

Therefore, $x=10$ is only the turning point.

$\frac{d^2 z}{d x^2}=7(35-x)^3\left(6 x^2-120 x+350\right)$

$\text { At } x=10, \frac{d^2 z}{d x^2}=7(35-10)^3(6 \times 100-120 \times 10+350)$

$=7(25)^3(-250)<0$

By second derivative test, $\frac{d z}{d x}$ will be maximum at $x=10$ when $y=35-10=25$ .

Therefore, the required numbers are 10 and 25.

Question:16) Find two positive integers whose sum is 16 and sum of whose cubes is minimum.

Solution: Consider the two positive numbers are $x$ and $y$ .

$x+y=16$

$y=16-x$

Let $z=x^3+y^3$

$z=x^3+(16-x)^3 \quad$ [From equation (i)]

$z=x^3+(16)^3-x^3-48 x(16-x)$

$=(16)^3-768 x+48 x^2$

Differentiate with respect to x

$\frac{d z}{d x}=-768+96 x$

And $\frac{d^2 z}{d x^2}=96$

Now $\frac{d z}{d x}= -768+96 x=0$

$x=8$

At $x=8, \frac{d^2 z}{d x^2}=96$ is positive.

$x=8$ is a point of local minima

$y=16-8=8$

Therefore, the required numbers are 8 and 8.

Question:17) A square piece of tin of side $18 \mathrm{~cm}$ is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?

Solution: Each side of square piece of tin is $18 \mathrm{~cm}$ .

Let $\mathrm{x} \mathrm{cm}$ be the side of each of the four squares cut off from each corner.

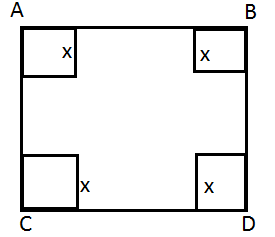
Then dimensions of the open box formed by folding the flaps after cutting off squares are $(18-2 x),(18-2 x)$ and $x \mathrm{cm}$ .

Let $z$ denotes the volume of the open box.

$z=(18-2 x)(18-2 x) x$

$z=(18-2 x)^2 x$

$z=\left(324+4 x^2-72 x\right) x$

$=4 x^3-72 x^2+324 x$

Differentiating with respect to x

$\frac{d z}{d x}=12 x^2-144 x+324 \text { and } \frac{d^2 z}{d x^2}=24 x-144$

$\text { Now } \frac{d z}{d x}=0$

$12x^2-144x+324=0$

$\Rightarrow x^2-12x +27=0$

$\Rightarrow x^2 -9x-3x+27=0$

$\Rightarrow x(x-9)-3(x-9)=0$

$\Rightarrow (x-3)(x-9)=0$

$\Rightarrow x = 3,9$

$x = 9$ is not possible

At $x = 3$

$\frac{d^2 z}{d x^2}=24 \times 3-144$

$= 72-144 = -72<0$

Volume of the box is maximum when $x = 3$ . Hence side of the square cut off from each corner

Question:18) A rectangula sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting of square from each corner and folding up the flaps. What should be the side of square to be cutt of so that the volume of the box is maximum?

Solution: Length and breadth of rectangular sheets 45 cm and 24 cm respectively.

Let side of each of the four squares cut off from each corner = x cm

Let Z denote the volume of the box

$Z = (45-2x)(24-2x)x$

$\Rightarrow Z = (1080-138x +4x^2)x$

$\Rightarrow Z = 1080x -138x^2+4x^3$

Now differentiating with respect to x

$\frac{dZ}{dx} = 1080 - 276x +12x^2$

and $\frac{d^2Z}{dx^2} = -276 +24x$

$\text { Now } \frac{d z}{d x}=0$

$12 x^2-276 x+1080=0$

$=x^2-23 x+90=0$

$(x-5)(x-18)=0$

$x=5 \text { or } x=18$

$x=18$ is rejected because at $x=18$ length $=24-2 x=18-2 \times 18=-12$ which is impossible.

Here $x=5$ is the turning point.

$\text { At } x=5, \frac{d^2 z}{d x^2}=24 \times 3-276=-156 \text { [Negative] }$

$z$ is maximum at $x=5$ that is, side of each square to be cut off from each corner for maximum volume is $5 \mathrm{~cm}$ .

Question:19) Show that of all the rectangles inscribed in a given fixed circle, the square has maximum area.

Solution: LetPQRS be the rectangle inscribed in a given circle with centre $\mathrm{O}$ and radius a.

Let $x$ and $y$ be the length and breadth of the rectangle, that is, $x>0$ and $y>0$
In right angled triangle $\mathrm{PQR}$ , using Pythagoras theorem,

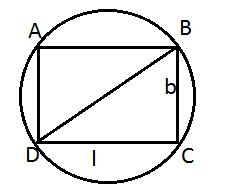
class 12 maths ex 6.5 ncert solution

$\mathrm{PQ}^2+\mathrm{QR}^2=\mathrm{PR}^2$

$x^2+y^2=(2 a)^2$

$y^2=4 a^2-x^2$

$y=\sqrt{4 a^2-x^2}$ –(i)

Let $\mathrm{A}$ be the area of the rectangle,

then $\mathrm{A}=\mathrm{xy}=x \sqrt{4 a^2-x^2}$

Squaring both side

$A^2 = S =x^2(4a^2-x^2)$

Differentiating with respect to x

$\frac{dS}{dx} = x^2(0-2x)+(4a^2-x^2).2x$

$= 2x(-x^2+4a^2-x^2)$

$= 2x(4a^2-2x^2)$ —–(ii)

For max and minima $\frac{dS}{dx} =0$

$2x(4a^2-2x^2)=0$

$\Rightarrow x = 0$ or $2x^2 = 4a^2$

$\Rightarrow x = 0$ or $x =\sqrt{2}a$

Again differentiate with respect to x of (ii)

$\frac{d^2S}{dx^2 } = 2x(-4x)+(4a^2-2x^2)$

$= -8x^2+4a^2-2x^2$

$= 4a^2-10x^2$

At $x = \sqrt{2}a$

$\frac{d^2S}{dx^2} = 4a^2 -10\times 2a^2$

$= 4a^2-20a^2=-16a^2<0$

Hence the area of the square is max when $x=\sqrt{2}a$

From eq (i)

$y=\sqrt{4 a^2-2a^2}$

$\Rightarrow y= 2a^2$

$x = y =\sqrt{2}$

Hence area of inscribed rectangle is maximum when it is a square

Question:20) Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.

Solution: Let $r$ be the radius of the circular base and $h$ be the height of closed right circular cylinder.

Formula for Total surface area $(\mathrm{S})=2 \pi r h+2 \pi r^2$

$S-2\pi r^2 = 2\pi rh$

$\Rightarrow h= \frac{S-2\pi r^2}{2\pi r}$ –(i)

Volume of cylinder $(V) = \pi r^2 h$

$V = \pi r^2(\frac{S-2\pi r^2}{2\pi r})$

$\Rightarrow V = \frac{1}{2}(Sr - 2\pi r^3)$

Differentiating with respect r

$\frac{dV}{dr} = \frac{1}{2}(S-6\pi r^2)$

And $\frac{d^2V}{dr^2} = \frac{1}{2}(0-12\pi r)=-6\pi r$

For max and minima $\frac{dV}{dr}= 0$

$\frac{1}{2}(S-6\pi r^2)=0$

$\Rightarrow S = 6\pi r^2$ .

Since $\frac{d^2V}{dr^2} = -6\pi r<0$

Hence volume of cylinder is max when $S = 6\pi r^2$

Value of S putting in equation (i)

$h= \frac{6\pi r^2-2\pi r^2}{2\pi r}$

$\Rightarrow h = \frac{4\pi r^2}{2\pi r} = 2r$

Height of cylinder = Diametre of cylinder

Hence volume of cylindr is max when $h = 2r$

Question:21) Of all the close cylindrical cans(right circular), of a given volume of 100 cubic centimeters, find the dimension of the can which has the minimum surface areas.

Solution : Let r be the radius and h be the height of the circular cylinder

Volume of the cylinder $(V) = \pi r^2 h$

$100 = \pi r^2 h$

$\Rightarrow h = \frac{100}{\pi r^2}$ — (i)

Total surface area

$S = 2\pi r h + 2\pi r^2$

$\Rightarrow S = 2\pi r( \frac{100}{\pi r^2})+2\pi r^2$

$\Rightarrow S = \frac{200}{r}+2\pi r^2$

Differentiate with respect to r

$\frac{dS}{dr}= -\frac{200}{r^2}+4\pi r$ —(ii)

For max and minima $\frac{dS}{dr}=0$

$-\frac{200}{r^2}+4\pi r = 0$

$\Rightarrow 4\pi r = \frac{200}{r^2}$

$\Rightarrow r^3 = \frac{200}{4\pi}$

$\Rightarrow r^3 = \frac{50}{\pi}$

$\Rightarrow r = (\frac{50}{\pi})^{1/3}$

Again differentiate with respect to r of eq (ii)

$\frac{d^2S}{d^2r}= -200(-2r^{-3})+4\pi$

$= \frac{400}{r^3}+4\pi$

At $r^3= \frac{50}{\pi}$

$\frac{d^2S}{d^2r} = \frac{400}{50/\pi}+4\pi$

$\Rightarrow \frac{d^2S}{dr^2}= 8\pi+4\pi=12\pi>0$

Total suface area is minimum when $r^3= \frac{50}{\pi}$

Hence from eq (i)

$h = \frac{100}{\pi r^2}$

$\Rightarrow h = \frac{100}{\pi(50/\pi)^{2/3}}$

$= \frac{2(50/\pi)}{(50/\pi)^{2/3}}$

$= 2(50/\pi)^{1-{2/3}}$

$= 2(50/\pi)^{1/3}$

$\Rightarrow h = 2r$

Question:22) A wire of length $28 \mathrm{~m}$ is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?

Solution: Let $\mathrm{x}$ meters be the side of square and $y$ meters be the radius of the circle.

Length of the wire $=$ Perimeter of square $+$ Circumference of circle

$4 x+2 \pi y=28$

$2 x+\pi y=14$

$y=\frac{14-2 x}{\pi}$

$\text { Area of square }=x^2 \text { and Area of circle }=\pi y^2$

$\text { Combined area }(\mathrm{A})=x^2+\pi y^2=x^2+\pi\left(\frac{14-2 x}{\pi}\right)^2$

$=x^2+\frac{4}{\pi}(7-x)^2$

$\frac{d \mathrm{~A}}{d x}=2 x-\frac{8}{\pi}(7-x) \text { and }$

$\frac{d^2 \mathrm{~A}}{d x^2}=2+\frac{8}{\pi}$

$\text { Now } \frac{d \mathrm{~A}}{d x}=0$

$2 x-\frac{8}{\pi}(7-x)=0$

$2 x=\frac{8}{\pi}(7-x)$

$2 \pi x=56-8 x$

$(2 \pi+8) x=56$

$x=\frac{56}{2 \pi+8}=\frac{28}{\pi+4}$

$\text { And } \frac{d^2 \mathrm{~A}}{d x^2}=2+\frac{8}{\pi} \text { [Positive] }$

$\text { A is minimum when } x=\frac{28}{\pi+4}$

Therefore, the length of one piece $4 x=\frac{112}{\pi+4}$

Lenghth of second piece $2\pi y= 28- \frac{28}{\pi+4}$

$= \frac{28\pi+112-112}{28+\pi}$

$= \frac{28\pi}{28+\pi}$

Question:23) Prove that the volume of the largest cone that can be inscribed in a sphere of radius $R$ is $\frac{8}{27}$ of the volume of the sphere.

Solution: Consider $O$ be the centre and $R$ be the radius of the given sphere, $O M$ $=x$

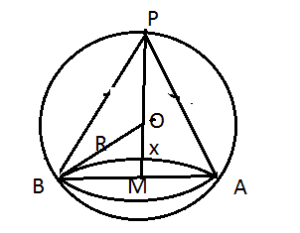
class 12 maths ex 6.5 ncert solution

In ΔOBM, using pythagoras theorem

$OB^2=OM^2+BM^2$

$\Rightarrow R^2 = x^2 + BM^2$

$\Rightarrow BM^2 = R^2-x^2$

$AM= h = R+x$

BM is the radius of cone

Volume of cone $V = \frac{1}{3}\pi r^2 h$

$\Rightarrow V = \frac{1}{3}\pi(R^2-x^2)(R+x)--(i)$

$\Rightarrow V = \frac{1}{3}\pi(R-x)(R+x)(R+x)$

$\Rightarrow V = \frac{1}{3}\pi (R-x)(R+x)^2$

Differentiating with respect to x

$\frac{dV}{dx} = \frac{1}{3}\pi [(R-x)2(R+x)+(R+x)^2(-1)]$

$= \frac{1}{3}\pi (R+x)[2(R-x)-(R+x)]$

$= \frac{1}{3}\pi(R+x)[2R-2x-R-x]$

$=\frac{1}{3}\pi (R+x)[R-3x]$ —(ii)

For max and minima $\frac{dV}{dx}=0$

$\frac{1}{3}\pi (R+x)[R-3x]=0$

Hence $R+x=0$ or $R-3x = 0$

$x = -R$ or $x = R/3$

$x =-R$ Not possible

Agian differentiate with respect to x of eq (ii)

$\frac{d^2V}{dx^2} = \frac{1}{3}\pi[(R+x)(-2)+(R-2x).1]$

$= \frac{1}{3}\pi[-2R-2x+R-2x]$

$= \frac{1}{3}\pi[-R-4x]$

At $x = R/3$

$\frac{d^V}{dx^2}=\frac{1}{3}\pi[-R-4\times \frac{R}{3}]$

$= \frac{1}{3}[-7R/3]<0$

Hence volume of cone is max when $x=R/3$

Now From eq (i)

$V = \frac{1}{3}\pi(R^2-\frac{R^2}{9})(R+\frac{R}{3})$

$= \frac{1}{3}\pi \frac{8R^2}{9}.\frac{4R}{3}$

$= \frac{8}{27}.\frac{4}{3}\pi R^3$

Volume of cone $= \frac{8}{27}\times$ volume of sphere

Question 24: Show that right circular cone of least curve surface and given volume has an altitude equal to $\sqrt{2}$ time the radius of the base

Solution: Let r be the radius of cone and h be the height of cone

Volume of cone $V= \frac{1}{3}\pi r^2 h$

$\Rightarrow h = \frac{3V}{\pi r^2}$ –(i)

Curve surface area of cone $S= \pi r l$

$S=\pi r\sqrt{r^2+h^2}$

$\Rightarrow S= \pi r\sqrt{r^2+(\frac{3V}{\pi r^2})^2}$

Squaring both side

$\Rightarrow S^2 =A= \pi^2r^2\left(r^2+\frac{9V^2}{\pi^2 r^4}\right)$

$A = \pi^2 r^4+\frac{9V^2}{r^2}$

Differentiating with respect to r

$\frac{dA}{dr} = 4\pi^2 r^3+9V^2(-2r^{-3})$

$\Rightarrow \frac{dA}{dr}= 4\pi^2 r^3 -\frac{18V^2}{r^3}---(ii)$

For max and minima $\frac{dA}{dr}=0$

$4\pi^2 r^3 -\frac{18V^2}{r^3}=0$

$\Rightarrow 4\pi^2 r^3 = \frac{18V^2}{r^3}$

$\Rightarrow 18V^2=4\pi^2 r^6$

$\Rightarrow V^2 = \frac{2}{9}\pi^2 r^6$

$\Rightarrow V = \frac{\sqrt{2}}{3}\pi r^3$

Again differentiate with respect to r of (ii)

$\frac{d^2V}{dr^2} = 12\pi^2 r^2 -18V^2(-3r^{-4})$

$= 12\pi^2 r^2+\frac{54V^2}{r^4}$

AT $V^2 = \frac{2}{9}\pi^2 r^6$

$\frac{d^2V}{dr^2} = 12\pi^2 r^2+\frac{54\times \frac{2}{9}\pi^2 r^6}{r^4}$

$= 12\pi^2 r^2 +12\pi^2 r^2= 24\pi^2r^2>0$

Hence curve surface area is minimum at $V=\frac{\sqrt{2}}{3}\pi r^3$

putting in (i)

$h = \frac{3\frac{\sqrt{2}}{3}\pi r^3}{\pi r^2}=\sqrt{2}r$

therefore height of the cone is $\sqrt{2}$ times the radius of base

Question:25) Show that the semi-vertical angle of the cone of the maximum value and of given slant height is $\tan ^{-1} \sqrt{2}$ .

Solution: Let $\mathrm{r}$ be the radius, $\mathrm{h}$ be the height, l be the slant height of given cone and $\theta$ be the semi-vertical angle of cone.

$l^2=r^2+h^2$

$r^2=l^2-h^2$

Formula for Volume of the cone $(\mathrm{V})=\frac{1}{3} \pi r^2 h$

$\mathrm{V}=\frac{1}{3} \pi\left(l^2-h^2\right) h$

$=\frac{\pi}{3}\left(l^2 h-h^3\right)$

$\frac{d \mathrm{~V}}{d h}=\frac{\pi}{3}\left(l^2-3 h^2\right)$

and

$\frac{d^2 \mathrm{~V}}{d h^2}=\frac{\pi}{3}(-6 h)=-2 \pi h$

$\text { Now } \frac{d \mathrm{~V}}{d h}=0$

$\frac{\pi}{3}\left(l^2-3 h^2\right)=0$

$l^2-3 h^2=0$

$3 h^2=l^2$

$h=\frac{l}{\sqrt{3}}$

$\text { At } h=\frac{l}{\sqrt{3}} \frac{d^2 \mathrm{~V}}{d h^2}=-2 \pi\left(\frac{l}{\sqrt{3}}\right)$

$=\frac{-2 \pi l}{\sqrt{3}} \text { [Negative] }$

$\mathrm{V} \text { is maximum at } h=\frac{1}{\sqrt{3}}$

$\text { From equation (1), } \quad r^2=l^2-\frac{l^2}{3}=\frac{2 l^2}{3}$

$r= \frac{\sqrt{2}l}{\sqrt{3}}$

$\tan \theta=\frac{r}{h}$

$\tan \theta = \frac{\frac{\sqrt{2}l}{\sqrt{3}}}{{\frac{l}{\sqrt{3}}}}=\sqrt{2}$

Which implies, $\theta=\tan ^{-1} \sqrt{2}$

Question:26) Show that the semi-vertical angle of the right circular cone of given surface area and maximum volume is $\sin ^{-1}\left(\frac{1}{3}\right)$

Solution: Let $\mathrm{r}$ be the radius and $\mathrm{h}$ be the height of the cone and semi-vertical angle be $\theta$ .

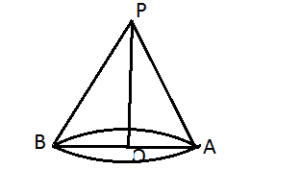
class 12 maths ex 6.5 ncert solution

Since, slant height $l^2 =r^2+h^2$

And, Total Surface area of cone (S) $= \pi rl+\pi r^2$

$S-\pi r^2 = \pi rl$

$\Rightarrow l = \frac{S-\pi r^2}{\pi r}---(i)$

Volume of cone $V=\frac{1}{3}\pi r^2 h$

$V= \frac{1}{3}\pi r^2\sqrt{l^2-r^2}$

Squaring both side

$\Rightarrow V^2 =A= \frac{1}{9}\pi^2 r^4(l^2-r^2)$

$\Rightarrow A= \frac{1}{9}\pi^2r^4\left((\frac{S-\pi r^2}{\pi r})^2-r^2\right)$

$\Rightarrow A = \frac{1}{9}\pi^2r^4\left[\frac{S^2+\pi^2r^4-2S\pi r^2}{\pi^2r^2}-r^2\right]$

$\Rightarrow A = \frac{1}{9}\pi^2r^4\left[\frac{S^2+\pi^2r^4-2S\pi r^2-\pi^2 r^4}{\pi^2r^2}\right]$

$\Rightarrow A = \frac{1}{9}\pi^2r^4\left[\frac{S^2-2S\pi r^2}{\pi^2r^2}\right]$

$\Rightarrow A= \frac{1}{9}\left[S^2r^2-2S\pi r^4\right]$

Differentiating with respect to r

$\frac{dA}{dr}= \frac{1}{9}[S^22r-8S\pi r^3]$

And $\frac{d^2A}{dr^2} =\frac{1}{9}[2S^2-24S\pi r^2]$

For max and minima $\frac{dA}{dr}=0$

$\frac{1}{9}[S^22r-8S\pi r^3]=0$

$\Rightarrow S^22r-8S\pi r^3=0$

$\Rightarrow 2S^2r = 8S\pi r^3$

$\Rightarrow S = 4\pi r^2$

At $S = 4\pi r^2$

$\frac{d^2A}{dr^2} =\frac{1}{9}[2S^2-24S\pi r^2]$

$= \frac{1}{9}2S[S-12\pi r^2]$

$= \frac{2}{9}S[4\pi r^2-12\pi r^2] = \frac{2}{9}S(-8\pi r^2)<0$

Hence Volume of cone is max when $S = 4\pi r^2$

Putting in eq (i)

$l = \frac{4\pi r^2-\pi r^2}{\pi r}= 3r$

In $\triangle OPA$

$\sin \theta = \frac{r}{l}$

$\Rightarrow \sin \theta = \frac{r}{3r}$

$\theta = \sin^{-1}(\frac{1}{3})$

Choose the correct answer in the Exercises 27 to 29.

Question:27) The point on the curve ${ }^{x^2=2 y}$ which is nearest to the point $(\mathbf{0}, \mathbf{5})$ is:

(A) $(2 \sqrt{2}, 2)$

(B) $(2 \sqrt{2}, 0)$

(D) $(2,2)$

Solution: Option (A) is correct.

Equation of the curve is $x^2=2 y$
Let $\mathrm{P}(\mathrm{x}, \mathrm{y})$ be any point on the curve (1), then according to question,

Distance between given point $(0,5)$ and $\mathrm{P}=\sqrt{(x-2)^2+(y-5)^2}=z$ (say)

$\Rightarrow z^2=x^2+(y-5)^2$

$=2 y+(y-5)^2 \quad \text { [From equation (1)] }$

$\Rightarrow z^2=2 y+y^2+25-10 y$

$\Rightarrow z^2=y^2-8 y+25=Z \text { (say) }$

$Rightarrow \frac{d Z}{d y}=2 y-8 \text { and } \frac{d^2 Z}{d y^2}=2$

$\text { Now } \frac{d Z}{d y}=0$

$\Rightarrow 2 y-8=0$

$\Rightarrow y=4$

$\text { At }y=4$

$\frac{d^2Z}{d y^2}=2 \text { [Positive] }$

$\therefore \mathrm{Z}$ is minimum and $z$ is minimum at $y=4$

From equation (1), we have $x^2=8$

$\Rightarrow x=\pm 2 \sqrt{2}$

$(2 \sqrt{2}, 4)$ and $(-2 \sqrt{2}, 4)$ are two points on curve (1) which are nearest to $(0,5)$ .

Question:28) For all real values of $\mathbf{x}$ , the minimum value of $\frac{1-x+x^2}{1+x+x^2}$ is:

(A) 0

(B) 1

(D) $1 / 3$

Solution: Option (D) is correct.

Given function is:

$f(x)=\frac{1-x+x^2}{1+x+x^2} \ldots \ldots \ldots(1)$

$\Rightarrow \quad f^{\prime}(x)=\frac{\left(1+x+x^2\right) \frac{d}{d x}\left(1-x+x^2\right)-\left(1-x+x^2\right) \frac{d}{d x}\left(1+x+x^2\right)}{\left(1+x+x^2\right)^2}$

$\Rightarrow \quad f^{\prime}(x)=\frac{\left(1+x+x^2\right)(-1+2 x)-\left(1-x+x^2\right)(1+2 x)}{\left(1+x+x^2\right)^2}$

$\Rightarrow \quad f^{\prime}(x)=\frac{-1+2 x-x+2 x^2-x^2+2 x^3-1-2 x+x+2 x^2-x^2-2 x^3}{\left(1+x+x^2\right)^2}$

$\Rightarrow \quad f^{\prime}(x)=\frac{-2+2 x^2}{\left(1+x+x^2\right)^2}=\frac{-2\left(1-x^2\right)}{\left(1+x+x^2\right)^2}$

$\text { Now } f^{\prime}(x)=0$

$\Rightarrow \frac{-2\left(1-x^2\right)}{\left(1+x+x^2\right)^2}=0$

$\Rightarrow^{-2}\left(1-x^2\right)=0$

$\Rightarrow 1-x^2=0$

$\Rightarrow x^2=1$

$\Rightarrow x=\pm 1$

$\therefore x=1 \text { and } x=-1 \text { [Turning points] }$

$\text { At } x=-1 \text {, }$

$\text { from equation (1), }$

$f(-1)=\frac{1+1+1}{1-1+1}=3$

$\text { At } x=1 \text {, }$

$f(1)=\frac{1-1+1}{1+1+1}=\frac{1}{3} \text { [Minimum value] }$

Question:29) The maximum value of $[x(x-1)+1]^{1 / 3}=0 \leq x \leq 1$ is:

(A) $\left(\frac{1}{3}\right)^{1 / 3}$

(B) $1 / 2$

(D) $1 / 3$

Solution: Option (C) is correct.

$\text { Consider } f(x)=[x(x-1)+1]^{\frac{1}{3}}$

$=\left(x^2-x+1\right)^{\frac{1}{3}}, 0 \leq x \leq 1 \ldots \ldots \ldots \text { (i) }$

$\therefore f^{\prime}(x)=\frac{1}{3}\left(x^2-x+1\right)^{\frac{-2}{3}} \frac{d}{d x}\left(x^2-x+1\right)$

$=\frac{(2 x-1)}{3\left(x^2-x+1\right)^{\frac{2}{3}}}$

Now $f^{\prime}(x)=0$

$\frac{(2 x-1)}{3\left(x^2-x+1\right)^{\frac{2}{3}}}=0$

$\Rightarrow 2 x-1=0$

Here ${x=\frac{1}{2}}$ is a turning point and it belongs to the given enclosed interval $0 \leq x \leq 1$ that is, $[0,1]$ . At $x=\frac{1}{2}$ , from equation (i),