A square piece of tin of side 18 cm is to be made into a box

Question 1:- A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?

Solution: Each side of square piece of tin is $18 \mathrm{~cm}$ .

Let $\mathrm{x} \mathrm{cm}$ be the side of each of the four squares cut off from each corner.

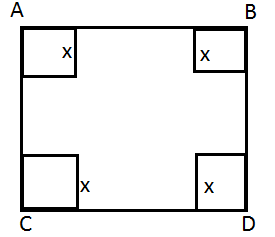
Then dimensions of the open box formed by folding the flaps after cutting off squares are $(18-2 x),(18-2 x)$ and $x \mathrm{cm}$ .

length(l) = 18-2x

breadth = 18-2x

height = x

Let $z$ denotes the volume of the open box.

$z=(18-2 x)(18-2 x) x$

$\Rightarrow z=(18-2 x)^2 x$

$\Rightarrow z=\left(324+4 x^2-72 x\right) x$

$=4 x^3-72 x^2+324 x$

Differentiating with respect to x

$\frac{d z}{d x}=12 x^2-144 x+324 \text { and } \frac{d^2 z}{d x^2}=24 x-144$

$\text { For max and minima } \frac{d z}{d x}=0$

$12x^2-144x+324=0$

$\Rightarrow x^2-12x +27=0$

$\Rightarrow x^2 -9x-3x+27=0$

$\Rightarrow x(x-9)-3(x-9)=0$

$\Rightarrow (x-3)(x-9)=0$

$\Rightarrow x = 3,9$

$x = 9$ is not possible

At $x = 3$

$\frac{d^2 z}{d x^2}=24 \times 3-144$

$= 72-144 = -72<0$

Volume of the box is maximum when $x = 3$ cm. Hence side of the square cut off from each corner

Question 2:- A rectangula sheet of tin 45 cm by 24 cmis to be made into a box without top, by cutting of square from each corner and folding up the flaps. What should be the side of square to be cutt of so that the volume of the box is maximum?

Solution:- For solution click here

Question 3:- Show that of all the rectangles inscribed in a given fixed circle, the square has maximum area.

Solution: For solution click here

https://gmath.in/class-12-maths-ex-6-5-ncert-solution/

Leave a Comment Cancel reply