Exercise 6.2(Linear Inequalities )
Solve the following inequalities graphically in two-dimensional plane:(Ex 6.2 Linear Inequalities ncert math solution class 11)
Question 1: x + y < 5
Solution: Given that ![]()
|
x |
0 | 5 |
| y | 5 |
0 |
Now, draw a dotted line x + y = 5 in the graph
Now, consider x + y < 5
Select a point (0, 0).
⇒ 0 + 0 < 5
⇒ 0 < 5 (this is true)
∴ The solution region of the given inequality is below the line x + y = 5. (That is, the origin is included in the region.)
The graph is as follows:

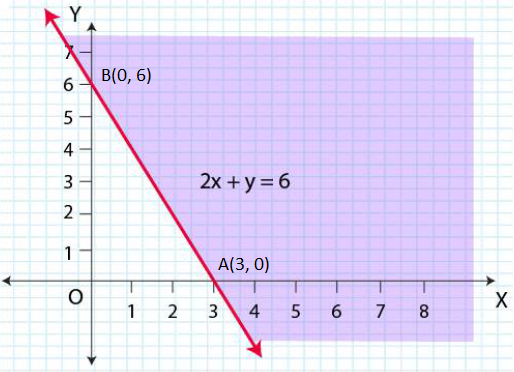
Question 2: 2x + y ≥ 6
Solution : Given that: 2x + y ≥ 6
|
x |
0 | 3 |
| y | 6 |
0 |
Now, draw a solid line 2x + y = 6 in the graph
Now, consider 2x + y ≥6
Select a point (0, 0).
⇒ 2 × (0) + 0 ≥ 6
⇒ 0 ≥ 6 (This is false.)
∴ The solution region of the given inequality is above the line 2x + y = 6. (Away from the origin.)
The graph is as follows:
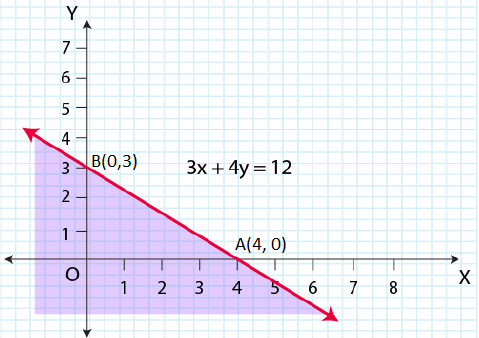
Question 3: 3x + 4y ≤ 12
Solution: Given that, 3x + 4y ≤ 12
|
x |
0 | 4 |
| y | 3 |
0 |
Now, draw a solid line 3x + 4y = 12 in the graph
Now, consider 3x + 4y ≤ 12
Select a point (0, 0).
⇒ 3 × (0) + 4 × (0) ≤ 12
⇒ 0 ≤ 12 (This is true.)
∴ The solution region of the given inequality is below the line 3x + 4y = 12. (That is, the origin is included in the region.)
The graph is as follows:
Question 4: y + 8 ≥ 2x
Solution: Given that, y + 8 ≥ 2x
|
x |
0 | 4 |
| y | -8 |
0 |
Now, draw a solid line y + 8 = 2x in the graph
Now, consider y + 8 ≥ 2x
Select a point (0, 0).
⇒ (0) + 8 ≥ 2 × (0)
⇒ 0≤ 8 (This is true.)
∴ The solution region of the given inequality is above the line y + 8 = 2x. (That is, the origin is included in the region.)
The graph is as follows:

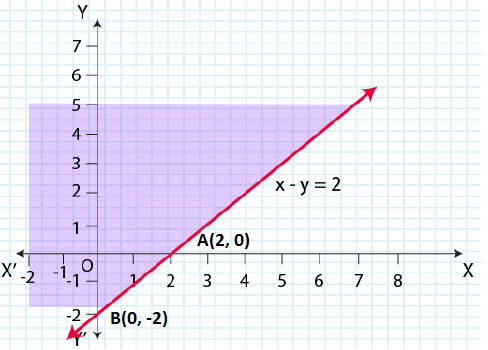
Question 5: x – y ≤ 2
Solution: Given that, x – y ≤ 2
|
x |
0 | 2 |
| y | -2 |
0 |
Now, draw a solid line x – y = 2 in the graph
Now, consider x – y ≤ 2
Select a point (0, 0).
⇒ (0) – (0) ≤ 2
⇒ 0 ≤ 2 (This is true.)
∴ The solution region of the given inequality is above the line x – y = 2. (That is, the origin is included in the region.)
The graph is as follows:
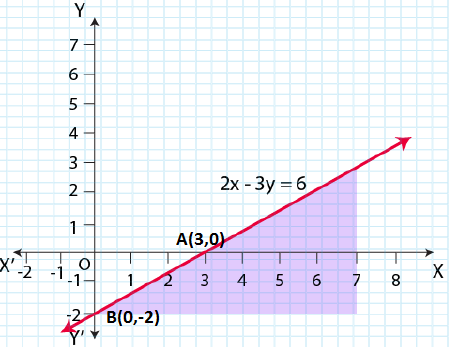
Question 6: 2x – 3y > 6
Solution: Given that, 2x – 3y > 6
Now, draw a dotted line 2x – 3y = 6 in the graph
Now, consider 2x – 3y > 6
Select a point (0, 0).
⇒ 2 × (0) – 3 × (0) > 6
⇒ 0 > 6 (This is false.)
∴ The solution region of the given inequality is below the line 2x – 3y > 6. (Away from the origin.)
The graph is as follows:
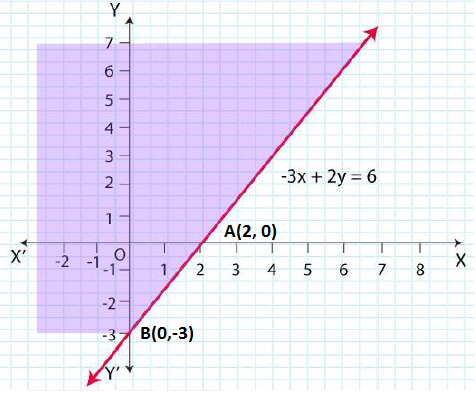
Question 7: – 3x + 2y ≥ – 6
Solution: Given that, – 3x + 2y ≥ – 6
Now, draw a solid line – 3x + 2y = – 6 in the graph
Now, consider – 3x + 2y ≥ – 6
Select a point (0, 0).
⇒ – 3 × (0) + 2 × (0) ≥ – 6
⇒ 0 ≥ – 6 (This is true.)
∴ The solution region of the given inequality is above the line – 3x + 2y ≥ – 6. (That is, the origin
is included in the region)
The graph is as follows:
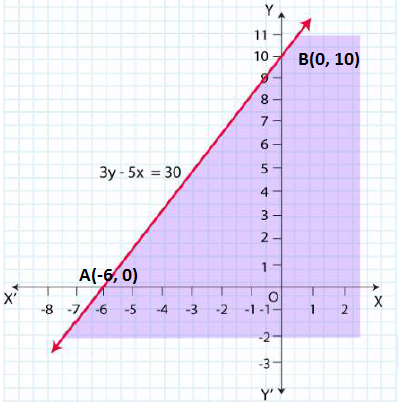
Question 8: 3y – 5x < 30
Solution: Given that, y – 5x < 30
|
x |
0 | -6 |
| y | 10 |
0 |
Now, draw a dotted line 3y – 5x = 30 in the graph
Now, consider 3y – 5x < 30
Select a point (0, 0).
⇒ 3 × (0) – 5 × (0) < 30
⇒ 0 < 30 (This is true.)
∴ The solution region of the given inequality is below the line 3y – 5x < 30. (That is, the origin is included in the region.)
The graph is as follows:
Question 9: y < – 2
Solution: Given that, y < – 2
Now, draw a dotted line y = – 2 in the graph
Now, consider y < – 2
Select a point (0, 0).
⇒ 0 < – 2 (This is false)
∴ The solution region of the given inequality is below the line y < – 2. (That is, away from the origin.)
The graph is as follows:

Question 10: x > – 3
Solution: Given that, x > – 3
Now, draw a dotted line x = – 3 in the graph
Now, consider x > – 3
Select a point (0, 0).
⇒ 0 > – 3
⇒ 0 > – 3 (This is true.)
∴ The solution region of the given inequality is right to the line x > – 3. (That is, the origin is included in the region.)
The graph is as follows:

Ex 6.1 Linear Inequalities ncert math solution class 11
Ex 6.2 Linear Inequalities ncert math solution class 11