EXERCISE 3.2(Trigonometric Function)
Find the values of other five trigonometric functions in Exercises 1 to 5.(Ex 3.2 Trigonomety ncert maths solution class 11)
Question 1: 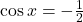 , x lies in third quadrant.
, x lies in third quadrant.
Solution: Given, ![]()
Since, ![]()
![]()
![]()
We know that
![]()
![]()
![]()
![]()
![]()
Since x lies in third quadrant
![]()
We know that
![]()
![]()
Since, ![]()
![]()
Now ![]()
![]()
Question 2: 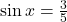 , x lies in second quadrant
, x lies in second quadrant
Solution: Given, ![]()
Since,![]()
![]()
We know that
![]()
![]()
![]()
![]()
X lies in second quadrant
![]()
Since, ![]()
![]()
Again we know that
![]()
![]()
And ![]()
![]()
Question 3: 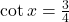 , x lies in third quadrant.
, x lies in third quadrant.
Solution: Given ![]()
Since, ![]()
![]()
We know that
![]()
![]()
![]()
![]()
x lies in third quadrant
![]()
Now, ![]()
![]()
Again we know that
![]()
![]()
![]()
![]()
![]()
x lies in third quadrant
![]()
Since, ![]()
![]()
Question 4: 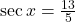 , x lies in fourth quadrant
, x lies in fourth quadrant
Solution: Given, ![]()
Sinc, ![]()
![]()
We know that
![]()
![]()
![]()
![]()
x lies in fourth quadrant
![]()
![]()
Since, ![]()
![]()
Since, ![]()
Question 5: 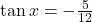 , x lies in second quadrant.
, x lies in second quadrant.
Solution: Given ![]()
Since ![]()
We know that
![]()
![]()
![]()
![]()
x lies in second quadrant
![]()
Now, ![]()
Again we know that
![]()
![]()
![]()
![]()
x lies in second quadrant
![]()
![]()
Find the values of the trigonometric functions in Exercises 6 to 10.
Question 6: sin 765°
Solution: The values of sin x repeat after an interval of 2π or 360°
So we get
![]()
![]()
![]()
question 7: 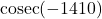
Solution: The values of sin x repeat after an interval of 2π or 360°
![]()
![]()
![]()
Question 8: 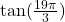
Solution: The values of sin x repeat after an interval of 2π or 360°
![]()
![]()
![]()
![]()
Question 9: 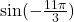
Solution: The values of sin x repeat after an interval of 2π or 360°
![]()
![]()
![]()
Question 10: 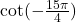
Solution: The values of sin x repeat after an interval of 2π or 360°
![]()
![]()
![]()
![]()
https://gmath.in/ex-3-1-trigonometric-function-ncert-solution-class-11/
