EXERCISE 4.1 ( Determinants )
Evaluate the determinant:(Class 12 ncert solution math exercise 4.1)
Question 1: ![]()
Solution: Let ![]()
Hence,
![]()
![]()
![]()
![]()
Question 2: Evaluate the determinants:
(i) ![]()
(ii) ![]()
Solution: (i) ![]()
![]()
![]()
![]()
(ii) ![]()
![]()
![]()
![]()
![]()
Question 3: If ![]() , then show that
, then show that ![]()
Solution: The given matrix is ![]()
Therefore,
![]()
![]()
Hence,
![]()
![]()
![]()
![]()
![]()
Now,
![]()
![]()
![]()
Therefore,
![]()
![]()
![]()
Thus, ![]() proved.
proved.
Question 4: If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{lll} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 4 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-13b073a7481eb213737962e58f3c84be_l3.png) , then show that
, then show that ![]()
Solution:The given matrix is
![Rendered by QuickLaTeX.com A=\left[\begin{array}{lll} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 4 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-13b073a7481eb213737962e58f3c84be_l3.png)
It can be observed that in the first column, two entries are zero. Thus, we expand along the first column ![]() for easier calculation.
for easier calculation.
![]()
![]()
![]()
Therefore,
![]()
![]()
Now,
![Rendered by QuickLaTeX.com 3 A=3\left[\begin{array}{lll} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 4 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-665c3475721aad703c59a9c5565f3517_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} 3 & 0 & 3 \\ 0 & 3 & 6 \\ 0 & 0 & 12 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-f7180e60ade27b30f1dca30e5d971a94_l3.png)
Therefore,
![]()
![]()
![]()
![]()
From equations ![]() and
and ![]() ,
,
![]()
Thus, ![]() proved.
proved.
Question 5:Evaluate the determinants
(i) 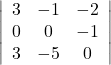
(ii) 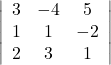
(iii) 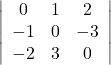
(iv) 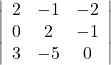
Solution: 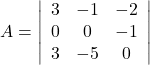
It can be observed that in the second row, two entries are zero. Thus, we expand along the second row for easier calculation.
Hence,
![]()
![]()
![]()
(ii) Let 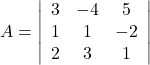
Hence,
![]()
![]()
![]()
![]()
![]()
(iii) Let 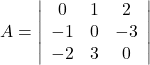
Hence,
![]()
![]()
![]()
![]()
(iv) 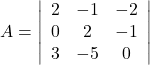
Hence,
![]()
![]()
![]()
Question 6:If ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc} 1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 & -9 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-29882662017163bc2e49ab56229401ea_l3.png) , find
, find ![]()
Solution: Let ![Rendered by QuickLaTeX.com A=\left[\begin{array}{ccc} 1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 & -9 \end{array}\right]](https://gmath.in/wp-content/ql-cache/quicklatex.com-29882662017163bc2e49ab56229401ea_l3.png)
Hence,
![]()
![]()
![]()
![]()
![]()
Question 7: Find the values of ![]() , if
, if
(i) ![]()
(ii) ![]()
Solution: (i) ![]()
![]()
![]()
![]()
![]()
![]()
Therefore,
(ii) ![]()
Therefore,
![]()
![]()
![]()
![]()
Question 8: If ![]() , the
, the ![]() is equal to
is equal to
(A) 6
(B) ![]()
(C) ![]()
(D) 0
Solution: ![]()
Therefore,
![]()
![]()
![]()
![]()
Thus, the correct option is B.