If tan inverse y/x = log root x^2 + y^2, then prove that

by

Question:

If \tan^{-1}(\frac{y}{x}) = \log \sqrt{x^2+y^2}, Prove that \dfrac{dy}{dx} = \dfrac{x + y}{x - y}.    ……..[CBSC 2020]

Solution:

Given, \tan^{-1}(\frac{y}{x}) = \log \sqrt{x^2+y^2}

\Rightarrow \tan^{-1}(\frac{y}{x}) = \frac{1}{2}\log (x^2 + y^2)

Differentiating with respect to x, we have,

\Rightarrow \dfrac{1 }{1+ (\frac{y}{x})^2}\times \left[\dfrac{x(\frac{y}{x})-1\times 1}{x^2}\right] = \dfrac{1}{2}\times \dfrac{1}{x^2+y^2}\times (2x + 2y(\frac{dy}{dx}))

\Rightarrow \dfrac{x^2}{x^2+y^2}\times \dfrac{\left(x\frac{dy}{dx}-y\right)}{x^2} = \dfrac{1}{x^2 + y^2}\left(x + y\frac{dy}{dx}\right)

\Rightarrow x\dfrac{dy}{dx} - y = x + y\dfrac{dy}{dx}

\Rightarrow (x - y)\dfrac{dy}{dx} = x + y

\Rightarrow \dfrac{dy}{dx} = \dfrac{x + y}{x - y}

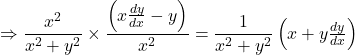
Some other question:

Q 1: If y^x = e^{(y-x)}, then prove that dy/dx = (1 + \log y)^2\log y

Q 2: Find the value of \dfrac{dy}{dx} at \theta = \dfrac{\pi}{4}, if x = ae^{\theta}(\sin \theta - \cos \theta) and y = ae^{\theta}(\sin \theta + \cos \theta).          ……..   [CBSC 2008, 2014]

Leave a Comment