EXERCISE 3.3 (Matrix)
class 12 maths exercise 3.3 solution
Question1: Find the transpose of each of the following matrices:
(i) ![]()
(ii) ![]()
(iii) 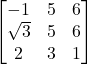
Solution: (i) Let 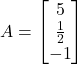
Then ![]()
(ii) Let ![]()
Then
![]()
(iii) Let 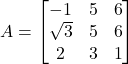
Then

Question2:  and
and Then verify that
Then verify that
(i) ![]()
(ii)![]()
Solution: (i) and
and 
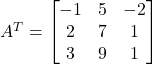
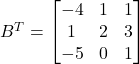
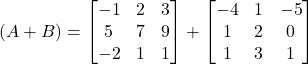
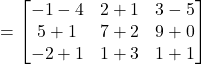
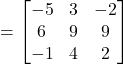
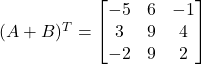
Now
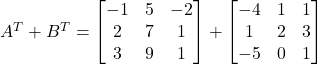
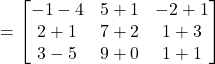
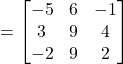
Hence ![]()
(ii) 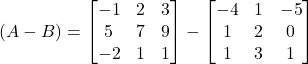
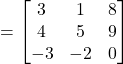
Then
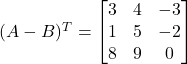
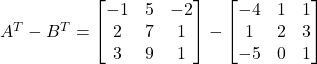

Thus
![]()
Question 5: For the matrices A and B, verify that![]()
(i) 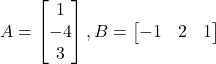
(ii) 
Solution: (i) It is given that 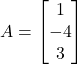 and
and ![]()
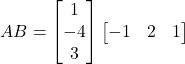

Therefore,
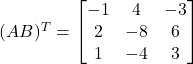
Now,
![]()
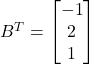
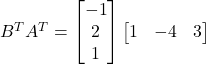
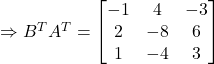
Thus,
![]()
(ii) It is given that 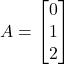 and
and ![]()
Hence
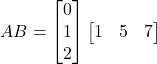
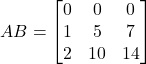
Therefore,
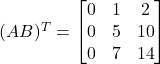
Now,
![]() and
and
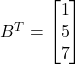
Therefore,
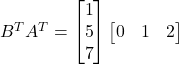

Thus,
![]()
Question 6: If (i) ![]() Then verify
Then verify ![]()
(ii)![]() Then verify
Then verify ![]()
Solution: (i) Since ![]()
Therefore,
![]()
Now,
![]()
![]()
![]()
Thus
![]()
(ii) It is given that ![]()
Therefore
![]()
Now
![]()
![]()
![]()
Thus
![]()
Question 7:(i) Show that the matrix 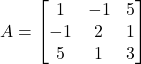 is a symmetric matrix.
is a symmetric matrix.
(ii) Show that the matrix 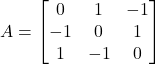 is a skew symmetric matrix.
is a skew symmetric matrix.
Solution: (i) Since 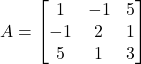
Now

![]()
Hence, A is a symmetric matrix.
(ii) 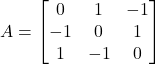

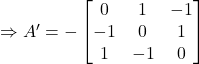
![]()
Hence, A is a skew symmetric matrix.
Question 8: For the matrix ![]() , verify that
, verify that
(i) ![]() is a symmetric matrix.
is a symmetric matrix.
(ii) ![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Solution: It is given that ![]()
![]()
Hence,
(i) ![]()
![]()
Therefore,
![]()
![]()
Thus (A+A’) is a symmetric matrix.
(ii) ![]()
![]()
Therefore,
![]()
![]()
Thus,![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Question 9: Find![]() and
and ![]() ,When
,When
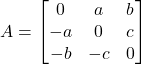
Solution: It is given that 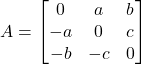
Hence,

Now,



Therefore,
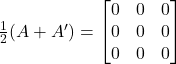
Now,

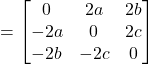
Thus,
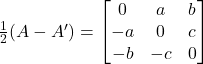
Question 10: Express the following as the sum of a symmetric and skew symmetric matrix:
(i) ![]()
(ii) 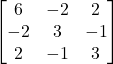
(iii) 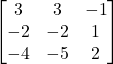
(iv) ![]()
Solution:(i) Let ![]()
Hence,
![]()
Now,
![]() +
+
![]()
Let,
P=![]()
![]()
![]()
Now,
P’=![]()
![]()
Thus,
P=![]() is a symmetric matrix.
is a symmetric matrix.
Now,
![]()
![]()
Let,
Q=![]()
![]()
![]()
Now,
![]()
![]()
![]()
![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Representing ![]() as the sum of P and Q:
as the sum of P and Q:
![]()
![]()
![]()
(ii) Let 
Hence,
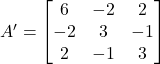
Now,
.

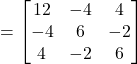
Let,
![]()

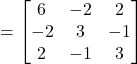
Now,

![]()
Thus ![]() is a symmetric matrix.
is a symmetric matrix.
Now,


Let,
![]()

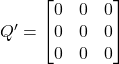
![]()
Thus, ![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Representing ![]() as the sum of
as the sum of ![]() and
and ![]() :
:
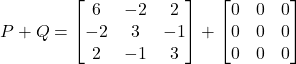
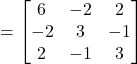
![]()
(iii) Let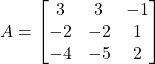
Hence,
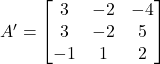
Now,
.

Let,
![]()
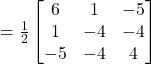
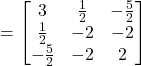
Now,
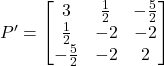
![]()
Thus ![]() is a symmetric matrix.
is a symmetric matrix.
Now,

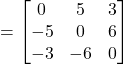
Let,
![]()

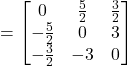
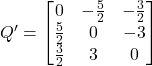

![]()
Thus, ![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Representing ![]() as the sum of
as the sum of ![]() and
and ![]() :
:
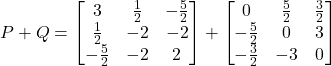
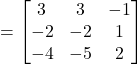
![]()
(iv) Let ![]()
Hence,
![]()
Now,
![]()
![]()
Let,
P=![]()
![]()
![]()
Now,
P’=![]()
![]()
Thus,
P=![]() is a symmetric matrix.
is a symmetric matrix.
Now,
![]()
![]()
Let,
Q=![]()
![]()
![]()
Now,
![]()
![]()
![]()
![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Representing ![]() as the sum of P and Q:
as the sum of P and Q:
![]()
![]()
![]()
Question 11: If ![]() are symmetric matrices of the same order, then
are symmetric matrices of the same order, then![]() is a
is a
(A) Skew symmetric matrix
(B) Symmetric matrix
(C) Zero matrix
(D) Identity matrix
Solution:The Correct option is ![]() .
.
If and are symmetric matrices of the same order, then
Solution: If ![]() and
and![]() are symmetric matrices of the same order, then
are symmetric matrices of the same order, then
![]() and
and ![]() —(1)
—(1)
Now consider,
![]()
![]()
![]()
![]()
Therefore,
![]()
Thus,![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Question 12: If ![]() then
then ![]() ,if the value of
,if the value of ![]() is:
is:
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
Solution:Thus, the correct option is ![]() .
.
It is given that
![]()
Hence,
![]()
NOW,
![]()
Therefore,
![]()
![]()
Comparing the corresponding elements of the two matrices, we have:
![]()
![]()
![]()


