Case study Chapter 4 (Determinant)
Case study 1:– Read the following and answer the questions(Case study problem determinant 1)

Three friends Rahul, Ravi and Rakesh went to a vegetable market to purchase vegetable. From a vegetable shop Rahul purchased 1 kg of each potato, onion and Brinjal for a total of Rs 21. Ravi purchased 4 kg of potato, 3 kg of onion and 2 kg of Brijal for ₹ 60 while Rakesh purchased 6 kg potato, 2 kg onion and 3 kg Brinjal for Rs 70
(i) If the cost of potato, onion and Brinjal are Rs x, Rs y and Rs z per kg respectively, then algebraic representation of given situation of problem is
(a) x + y + z = 6, x + y + 3z = 11, 3x + 2y + z = 2
(b) x + y + z = 21, 4x + 3y + 2z = 60, 6x + 2y + 3z = 70
(c) 2x + 3y + z = 21, x + y + z = 60, x + 2y + z = 70
(d) x + y + z = 70, 4x + 2y + 2z = 21, 6x + 2y + 3z =6
(ii) The algebraic representation obtained in question (i) is represented in matrix-system as
(a) 
(b) 
(c) 
(d) 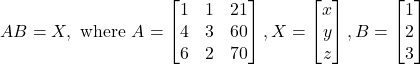
(iii) If Ax = B, where A, X, B are matrix then X should be
(a) X = AB (b) X = BA
(c) $X = A^{-1}B$ (d) $X = AB^{-1}$
(iv) If 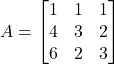 then
then ![]() is
is
(a) 
(b) 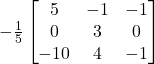
(c) 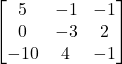
(d) 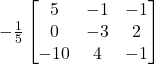
(v) The cost of potato, onion and Brinjal are
(a) Rs 5, Rs 8 and Rs 8 (b) Rs 4, Rs 8 and Rs 11
(c) Rs 4,Rs 11 and Rs 10 (d) Rs 4,Rs 8 and Rs 15
Solution (i) answer(b)
From question
For Rahul x + y + z = 21
For Ravi 4x + 3y + 2z = 60
For Rakesh 6x + 2y + 3z = 70
Therefore algebraic representaion is
x + y + z = 21
4x + 3y + 2z = 60
6x + 2y + 3z = 70
(ii) Answer (a)
The given algebraical system of linear question can be written in matrix system as
AX = B
where, A is coefficient matrix
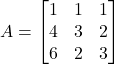
X is variable matrix
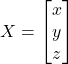
and B is a constant matrix
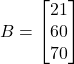
(iii) Answer (c)
We have AX = B
Pre multiplying by ![]() on both sides, we have
on both sides, we have
![]()
![]()
![]()
![]()
(iv) Answer (d)
We have
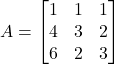
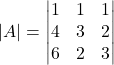
![]()
![]()
Now,
![]()
![]()
![]()
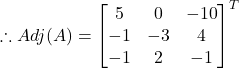
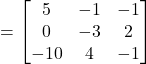
![]()
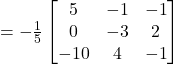
(v) Answer (a)
We have
![]()

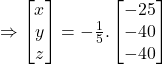
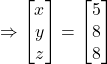
Hence x = 5, y = 5, and z = 8
Cost of potato,onion and brinjal are ₹5, ₹8 and ₹8.
Some other Case study problem
Case study 2:- Read the following and answer the question(Case study problem determinant 2)
Reshma wants to donate a rectangular plot of land for a school of her village. When she was asked by construction agency to give dimensions of the plot, she said that if its length is decreased by 50 m and breadth is increased by 50m, then its area will remain same, but if length is decreased by 10 m and breadth is decreased by 20m, then its area will decreased by 5300 m².

(i) If length of recangular plot of land be x m and breadth y m then the situation described in problem may be written in system of linear equation as
Solution: For solution click here
Case study 3:– Read the following and answer the question(Case study problem determinant 3 )
The monthly incomes of two sister Reshma and Ritam are in the ratio 3:4 and their monthly expenditures are in the ratio 5:7. Each sister saves Rs 15,000 per month.

Solution : For solution click here
Case study 4:– Read the following and answer the question(Case study problem determinant 4)
On the occasion of children’s day. Class teacher of class XII shri singh, decided to donate some money to students of class XII.

If there were 8 studens less, every one would have got Rs 10 more, however if there were 16 students more, everyone would have got Rs 10 less.
Solution: For solution click here
Case study 5:– In coaching institutes, the students not only get academic guidance but also they get to know about career options and right goals as per their interest and academic record.(Case study problem determinant 5)

A coaching institute conduct classes in two sections A and Band fees for rich and poor children are different. In section A, there are 20 poor and 5 rich children and total monthly collection is ₹9,000, where as in section B, there are 5 poor and 25 rich children and total monthly collection is ₹ 26, 000.
Solution: For solution click here


