Trigonometry formulae for class 11

The word ‘trigonometry’ is derived from the Greek words ‘trigon’ and ‘metron’ and it means ‘measuring the sides of a triangle’. The subject was originally developed to solve geometric problems involving triangles. It was studied by sea captains for navigation, surveyor to map out the new lands, by engineers and others(Trigonometry formulae for class 11)

In earlier classes, we have studied the trigonometric ratios of acute angles as the ratio of the sides of a right angled triangle. We have also studied the trigonometric identities and application of trigonometric ratios in solving the problems related to heights and distances.

You see these formulae in the given link

Trigonometric formulae for class 10

Relation between degree and radian

A circle subtends at the centre an angle whose radian measure is 2π and its degree measure is 360°

Then, 2 π Radian = 360°

⇒ $1 \text{Radian} = \dfrac{360}{2\pi}$ degree

Now, $1 \text{Radian} = \dfrac{180}{\pi} = 57^\circ 16'$ approximately

And $1^\circ = \dfrac{\pi}{180}$ Radian = 0.01746 radian approximately

Relation between arc length, Radius and Angle(In Radian)

Since in a circle of radius r, an arc of length l subtends an angle whose measure is θ(In Radian)

Then, l = r × θ or θ = l/r

Trigonometric Functions

(1) Sin x = 1/Cosec x (2) cosec x = 1/Sin x

(3) Cos x = 1/Sec x (4) Sec x = 1/cos x

(5) Tan x = 1/Cot x (6) Cot x = 1/Tan x

(7) Tan x = Sin x/Cos x (8) Cot x = Cos x/Sinx

(9) (i) Sin²x + Cos²x = 1

(ii) Sin²x = 1 – Cos²x

(iii) Cos²x = 1 – Sin²x

(10)(i) Sec²x = 1 + Tan²x

(ii) Sec²x – Tan²x = 1

(iii) Tan²x = Sec²x – 1

(11) (i) Cosec²x = 1 + Cot²x

(ii) Cosec²x – Cot²x = 1

(iii) Cot²x = Cosec²x – 1

(12) sin x = 0 implies x = nπ, where n is any integer

(13) cos x = 0 implies x = (2n + 1)π/2, where n is any integer

Trigometry value table

Sign of trigonometric functions

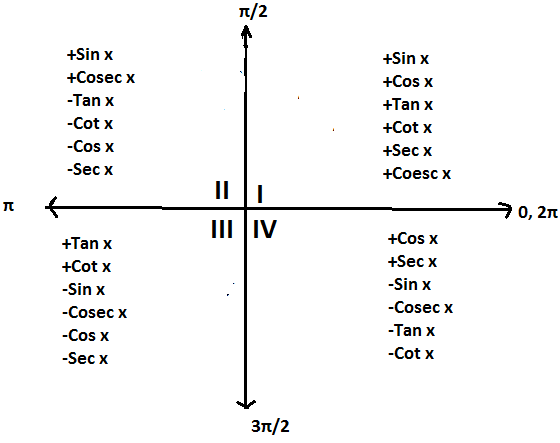
Range of Trigonometric function in quadrant

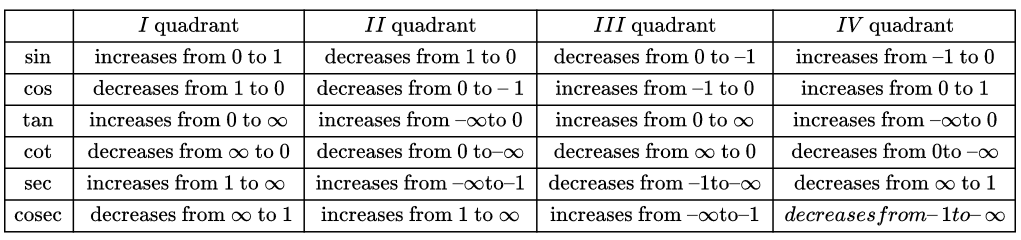
Domain and Range of Trigonometric function

When we add or subtract 2π to any trigonometric function then the value of that function remain unchanged

For example : (i) Sin θ = Sin(2π + θ) (ii) Sin θ = Sin (θ – 2 π)

(iii) Cos 765° =Cos(45 + 2× 360)

⇒ Cos 45 = 1/√2

Trigonometric Functions of Sum and Difference of Two Angles

Example: (i) Sin(π/2 – x)

(π/2 – x) lies in Ist quadrant and ‘Sin’ function remain positive in Ist quadrant

Value of Sin x will change to Cos x

Then the value of ‘Sin(π/2 – x) = Cos x’

Some other formulae

1.(i) $\sin(-x) = -\sin x$ (ii) $\cos(-x)= \cos x$

(iii) $\tan(-x) = -\tan x$ (iv) $\cot(-x) = -\cot x$

(v) $\sec(-x) = \sec x$ (vI) $\operatorname{cosec}(-x)= -\operatorname{cosec}x$

2.(i) $\sin(\frac{\pi}{2}-x) = \cos x$ (ii) $\cos(\frac{\pi}{2}-x) = \sin x$

(iii) $\tan(\frac{\pi}{2}-x) = \cot x$ (iv) $\cot(\frac{\pi}{2}-x) = \tan x$

(v) $\sec(\frac{\pi}{2}-x) = \operatorname{cosec} x$ (vi) $\operatorname{cosec}(\frac{\pi}{2}-x) = \sec x$

3. (i) $\sin(\frac{\pi}{2}+x) = \cos x$ (ii) $\cos(\frac{\pi}{2}+x) = -\sin x$

(iii) $\tan(\frac{\pi}{2}+x) = -\cot x$ (iv) $\cot(\frac{\pi}{2}+x) = -\tan x$

(v) $\sec(\frac{\pi}{2}+x) = -\operatorname{cosec} x$ (vi) $\operatorname{cosec}(\frac{\pi}{2}+x) = \sec x$

4.(i) $\sin(\pi - x) = \sin x$ (ii) $\cos(\pi-x) = -\cos x$

(iii) $\tan(\pi - x) = -\tan x$ (iv) $\cot(\pi-x) = -\cot x$

(v) $\sec(\pi - x) = -\sec x$ (vi) $\operatorname{cosec}(\pi-x) = \operatorname{cosec}x$

5. (i) $\sin(\pi +x) = -\sin x$ (ii) $\cos(\pi + x) = -\cos x$

(iii) $\tan (\pi + x) = \tan x$ (iv) $\cot(\pi + x) = \cot x$

(v) $\sec(\pi +x) = -\sec x$ (vi) $\operatorname{cosec}(\pi + x) = -\operatorname{cosec}x$

6. (i) $\sin(\frac{3\pi}{2}-x) = -\cos x$ (ii) $\cos(\frac{3\pi}{2}-x) = -\sin x$

(iii) $\tan(\frac{3\pi}{2}-x) = \cot x$ (iv) $\cot(\frac{3\pi}{2}-x) = \tan x$

(v) $\sec(\frac{3\pi}{2}-x) = -\operatorname{cosec} x$ (vi) $\operatorname{cosec}(\frac{3\pi}{2}-x) = -\sec x$

7.(i) $\sin(\frac{3\pi}{2}+x) = -\cos x$ (ii) $\cos(\frac{3\pi}{2}+x) = \sin x$

(iii) $\tan(\frac{3\pi}{2}+x) = -\cot x$ (iv) $\cot(\frac{3\pi}{2}+x) = -\tan x$

(v) $\sec(\frac{3\pi}{2}+x) = \operatorname{cosec} x$ (vi) $\operatorname{cosec}(\frac{3\pi}{2}+x) = -\sec x$

8.(i) $\sin(2\pi - x) = -\sin x$ (ii) $\cos(2\pi-x) = \cos x$

(iii) $\tan(2\pi - x) = -\tan x$ (iv) $\cot(2\pi-x) = -\cot x$

(v) $\sec(2\pi - x) = \sec x$ (vi) $\operatorname{cosec}(2\pi-x) = -\operatorname{cosec}x$

9.(i) $\sin(2\pi +x) = \sin x$ (ii) $\cos(2\pi + x) = \cos x$

(iii) $\tan (2\pi + x) = \tan x$ (iv) $\cot(2\pi + x) = \cot x$

(v) $\sec(\pi +x) = \sec x$ (vi) $\operatorname{cosec}(2\pi + x) = \operatorname{cosec}x$

10.(i) $\sin(x+y)=\sin x\cos y+\cos x\sin y$

(ii) $\sin(x-y)=\sin x\cos y-\cos x\sin y$

(iii) $\cos(x + y) = \cos x\cos y - \sin x\sin y$

(iv) $\cos (x - y) = \cos x\cos y + \sin x\sin y$

(v) $\tan(x + y) = \dfrac{\tan x + \tan y}{1-\tan x.\tan y}$

(vi) $\tan(x - y) = \dfrac{\tan x - \tan y}{1 + \tan x.\tan y}$

(vii) $\cot(x + y)) = \dfrac{\cot x.\cot y-1}{\cot y + \cot x}$

(viiii) $\cot(x - y) = \dfrac{\cot x.\cot y+1}{\cot y - \cot x}$

11. (i) $\sin 2x =2\sin x\cos x$

(ii) $\sin 2x = \dfrac{2\tan x}{1+\tan^2x}$

12. (i) $\cos 2x = \cos^2x - \sin^2x$

(ii) $\cos 2x = 1 - 2\sin^2x$

(iii) $\cos 2x = 2\cos^2x - 1$

(iv) $\cos 2x = \dfrac{1 - \tan ^2x}{1 + \tan^2x}$

13. $\tan 2x = \dfrac{2\tan x}{1 - \tan^2x}$

14. $\sin 3x = 3\sin x - 4\sin^3x$

15. $\cos 3x = 4\cos^3x - 3\cos x$

16. $\tan 3x = \dfrac{3\tan x - \tan^3x}{1 - 3\tan^2x}$

17. (i) $\sin x =2\sin \frac{x}{2}\cos\frac{x}{2}$

(ii) $\sin x = \dfrac{2\tan \frac{x}{2}}{1+\tan^2\frac{x}{2}}$

18. ( i) $\cos x = \cos^2\frac{x}{2} - \sin^2\frac{x}{2}$

(ii) $\cos x = 1 - 2\sin^2\frac{x}{2}$

(iii) $\cos x = 2\cos^2\frac{x}{2} - 1$

(iv) $\cos x = \dfrac{1 - \tan ^2\frac{x}{2}}{1 + \tan^2\frac{x}{2}}$

19. $\tan x= \dfrac{2\tan \frac{x}{2}}{1 - \tan^2\frac{x}{2}}$

20. (i) $1 + \cos 2x = 2\cos^2x$

(ii) $1-\cos 2x = 2\sin^2 x$

21. (i) $1 +\cos x = 2\cos^2 \frac{x}{2}$

(ii) $1 - \cos x = 2\sin^2\frac{x}{2}$

22. (i) $\sin x + \sin y = 2\sin\dfrac{x + y}{2}\cos \dfrac{x - y}{2}$

(ii) $\sin x - \sin y = 2\cos\dfrac{x + y}{2}\sin \dfrac{x - y}{2}$

(iii) $\cos x + \cos y = 2\cos\dfrac{x + y}{2}\cos \dfrac{x - y}{2}$

(iv) $\cos x - \cos y = -2\sin\dfrac{x + y}{2}\sin \dfrac{x - y}{2}$

23. (i) $2\sin x\cos y = \sin (x + y) +\sin(x - y)$

(ii) $2\cos x \sin y = \sin(x + y) - \sin(x - y)$

(iii) $2\cos x \cos y = \cos(x + y)+\cos(x-y)$

(iv) $2\sin x\sin y = \cos(x -y ) - \cos (x + y)$ )

Trigonometric formulae for class 10

Class 10 Case study Chapter 8 introduction to Trigonometry

From ncert.nic.in

Some other formulae

Leave a Comment Cancel reply