inverse trigonometric formulae

by

Inverse trigonometry formulae play a vital role in solving a variety of mathematical and real-world problems. These formulas, such as arcsin, arccos, and arctan, allow us to find the angles associated with specific trigonometric ratios. They are essential tools for trigonometric calculations involving triangles, physics, engineering, and more.

Inverse Trigonometric Formulae Class 12

1. sin^{-1}x should not be confused with (sin x)^{-1}. In fact (sin x)^{-1} =\frac{1}{sin x} and similarly for other trigonometric functions.

2. Whenever no branch of an inverse trigonometric functions is mentioned, we mean the principal value branch of that function.

3. The value of an inverse trigonometric functions which lies in the range of principal branch is called the principal value of that inverse trigonometric functions.

The following table gives the inverse trigonometric function (principal value branches) along with their domains and ranges

\begin{array}{|c|c|c|} \hline \text { Function } & \text { Domain } & \text { Range } \\ \hline \sin ^{-1}x & {[-1,1]} & {[-\pi / 2, \pi / 2]} \\ \hline \cos ^{-1} x& {[-1,1]} & {[0, \pi]} \\ \hline \tan ^{-1}x & R & {[-\pi / 2, \pi / 2)} \\ \hline \cot ^{-1} x& R & {[0, \pi]} \\ \hline \sec ^{-1}x & \mathbb{R}-(-1,1] & {[0, \pi]-\{\pi / 2\}} \\ \hline \operatorname{cosec}^{-1} x& R-[-1,1) & {[-\pi / 2, \pi / 2]-\{0\}} \\ \hline \end{array}

Inverse trigonometric formulae

(1) (a) \sin ^{-1}\left(\frac{1}{x}\right)=\operatorname{cosec}^{-1} x ; x \geq 1 or x \leq-1

(b) \cos ^{-1}\left(\frac{1}{x}\right)=\sec ^{-1} x ; x \geq 1 or x \leq-1

(c) \tan ^{-1}\left(\frac{1}{x}\right)=\left\{\begin{array}{c}\cot ^{-1} x ; x>0 \\ -\pi+\cot ^{-1} x ; x<0\end{array}\right.

(2) (a) \sin ^{-1}(-x)=-\sin ^{-1} x ; x \in[-1,1]

(b) \tan ^{-1}(-\mathrm{x})=-\tan ^{-1} \mathrm{x} ; \mathrm{x} \in R

(c) \operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1} x i |x| \geq 1

(3) (a) \cos ^{-1}(-\mathrm{x})=\pi-\cos ^{-1} \mathrm{x} ; \mathrm{x} \in[-1,1]

(b) \sec ^{-1}(-x)=\pi-\sec ^{-1} x; |x| \geq 1

(c) \cot ^{-1}(-\mathrm{x})=\pi-\cot ^{-1} \mathrm{x} ; \mathrm{x} \in R

(4) (a) \sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2} ; x \in[-1,1]

(b) \tan ^{-1} \mathrm{x}+\cot ^{-1} \mathrm{x}=\frac{\pi}{2} ; \mathrm{x} \in R

(c) \operatorname{cosec}^{-1} x+\sec ^{-1} x=\frac{\pi}{2} i |x| \geq 1

(5) (a) \tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right) ; x y<1

(b) \tan ^{-1} x-\tan ^{-1} y=\tan ^{-1}\left(\frac{x-y}{1+x y}\right) ; x y>-1

(6) (a) 2 \tan ^{-1} x=\sin ^{-1}\left(\frac{2 x}{1+x^2}\right) i |x| \leq 1

(b) 2 \tan ^{-1} x=\cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right) ; x \geq 0

(c) 2 \tan ^{-1} \mathrm{x}=\tan ^{-1}\left(\frac{2 \mathrm{x}}{1-\mathrm{x}^2}\right) ;-1<\mathrm{x}<1

(d) 2 \sin ^{-1} x=\sin ^{-1}\left(2 x \sqrt{1-x^2}\right) ; \frac{-1}{\sqrt{2}} \leq x \leq \frac{1}{\sqrt{2}}

(d) 2 \cos ^{-1} x=\sin ^{-1}\left(2 x \sqrt{1-x^2}\right) ; \frac{-1}{\sqrt{2}} \leq x \leq

(e) 2 \cos ^{-1} x=\cos ^{-1}\left(2 x^2-1\right) ; 0 \leq x \leq 1

(7) (a) \sin ^{-1} x+\sin ^{-1} y=\sin ^{-1}\left(x \sqrt{1-y^2}+y \sqrt{1-x^2}\right)

(b) \sin ^{-1} x-\sin ^{-1} y=\sin ^{-1}\left(x \sqrt{1-y^2}-y \sqrt{1-x^2}\right)

(c) \cos ^{-1} x+\cos ^{-1} y=\cos ^{-1}\left(x y-\sqrt{1-x^2} \sqrt{1-y^2}\right)

(d) \cos ^{-1} x-\cos ^{-1} y=\cos ^{-1}\left(x y+\sqrt{1-x^2} \sqrt{1-y^2}\right)

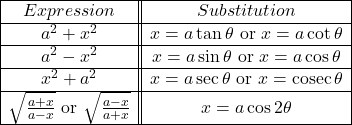
8. Important substitution to simply trigonometrical expression involving inverse trigonometrical functions.

\begin{array}{|c||c|}\hline Expression & Substitution\\\hline a^2+x^2 & x=a\tan\theta \text{ or }x=a\cot\theta \\ \hline a^2-x^2& x=a\sin\theta\text{ or } x=a\cos\theta\\\hline x^2+a^2&x=a\sec\theta\text{ or }x=\operatorname{cosec}\theta\\\hline \sqrt{\frac{a+x}{a-x}}\text{ or } \sqrt{\frac{a-x}{a+x}} & x=a\cos2\theta\\ \hline \end{array}

Chapter 2 Inverse Trigonometry

Class 12 ncert solution math exercise 2.1

Class 12 ncert solution math exercise 2.2

Class 12 ncert solution math chapter 2 Miscellaneous

Leave a Comment