EXERCISE 3.2 (MATRIX)
Class 12 ncert solution math exercise 3.2 matrix
Question 1: A=![]() ,B=
,B=![]() ,C=
,C=![]()
Find each of the following
(a)![]()
(b)![]()
(c)![]()
(d)![]()
(e)![]()
Solution:(a)![]()
![]()
![]()
![]()
(b)![]()
![]()
![]()
![]()
(c)![]()
![]()
![]()
![]()
(d) ![]()
![]()
![]()
![]()
![]()
(e) ![]()
![]()
![]()
![]()
![]()
Question 2: Compute the following:
(a)![]()
(b)![]()
(c) 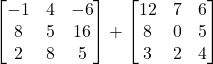
(d) ![]()
Solution: (a) ![]()
![]()
![]()
(b) ![]()
![]()
![]()
(c) 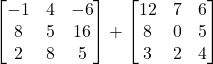
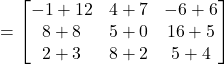

(d) ![]()
![]()
![]()
Question 3: Compute the indicated products:
(a) ![]()
(b)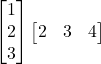
(c)![]()
(d)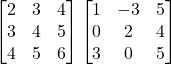
(e)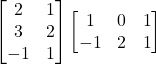
(f)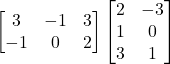
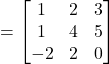
Solution: (a)![]()
![]()
![]()
![]()
(b)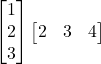
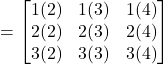

(c)![]()
![]()
![]()
![]()
(d) 
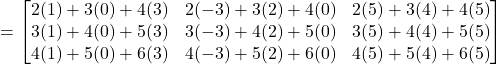

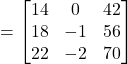
(e)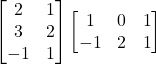
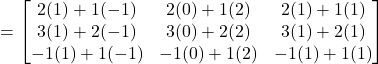
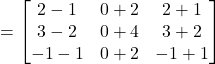
(f)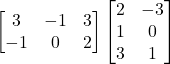
![]()
![]()
![]()
Question 4: If 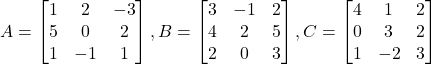
Then compute A+B and B-C. Also, verify that A+(B+C)=(A+B)-C
Solution: 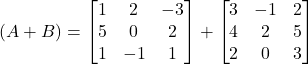
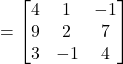

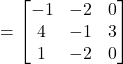
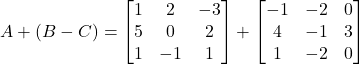



Hence, A+(B-C)=(A+B)-C
Question 5: If  and
and 
Solution: 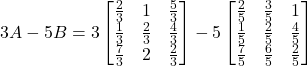


Question 6: ![]()
Solution: ![]()
![]()
![]()
Question 7: Find X and Y,if
(a)![]() and
and ![]()
(b)![]() and
and
![]()
Solution: (a) ![]()
![]()
Adding equation (1) and (2)
![]()
![]()
![]()
![]()
Since
![]()
![]()
![]()
(b) ![]()
![]()
Multiplying equation (1) by 2and multiplying (2) by 3
![]()
![]()
subtracting (3) to (4)
![]()
![]()
![]()
![]()
Now,
![]()
![]()
![]()
![]()
![]()
Question 8: ![]()
Solution: Since ![]()
![]()
![]()
![]()
![]()
![]()
Question 9:Find x and y ,if ![]()
Solution: Since
![]()
![]()
![]()
Comparing the corresponding elements two matrices:
![]()
![]()
![]()
![]()
Therefore x=3 and y=3
Question 10: Solve the equation for x,y,z, and t if ![]()
Solution: ![]()
![]()
![]()
Comparing the corresponding elements two matrices:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence the values of x=3,y=6,z=9 and t=6
Question 11: If ![]()
Findthe value of x and y
Solution: ![]()
![]()
![]()
Comparing the corresponding elements two matrices:
![]()
![]()
Adding (1)and (2) equation
![]()
![]()
put the value of x in (1) Equation
![]()
![]()
![]()
![]()
Hence the value of x=3 and y=-4
Question 12: Given
![]() Find the value of x,y,z and w.
Find the value of x,y,z and w.
Solution :![]()
![]()
Comparing the corresponding elements two matrices:
![]()
![]()
![]()
Since
![]()
![]()
![]()
![]()
![]()
Since
![]()
![]()
Since
![]()
![]()
![]()
![]()
![]()
Therefore x=2,y=4,z=1 and w=3
Question 13: If 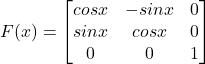 Show that
Show that ![]() .
.
Solution: 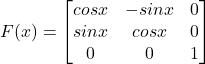 and
and 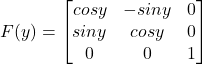
Now
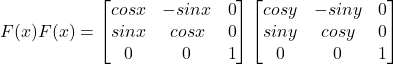
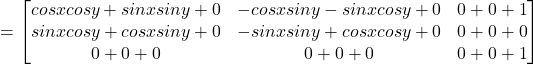

![]()
Hence F(x)F(y)=F(x+y)
Question 14: Show that (a)![]()
(b) 
Solution: (a)![]()
LHS.
![]()
![]()
![]()
RHS.
![]()
![]()
![]()
Therefore ,![]()
(b) 
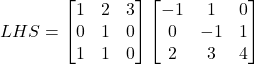
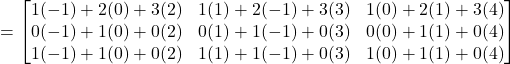
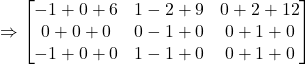
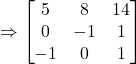

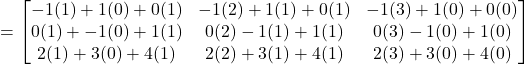
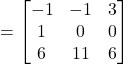
Therefore, ![]()
Question 15. Find ![]() , if
, if 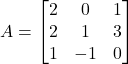
Solution: Since 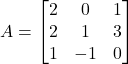
![]()

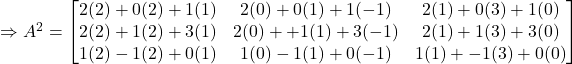
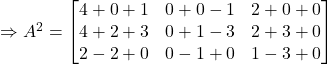
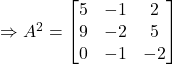
Therefore,
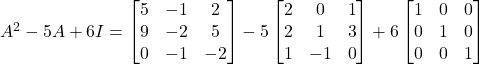
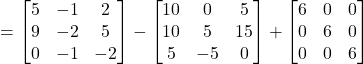
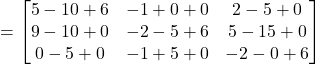
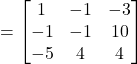
Question 16: If 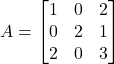 , Prove that
, Prove that ![]()
Solution: 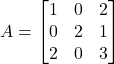
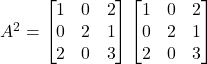
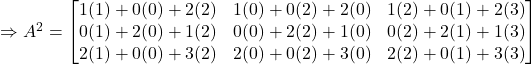
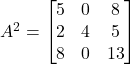
![]()

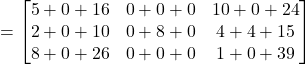

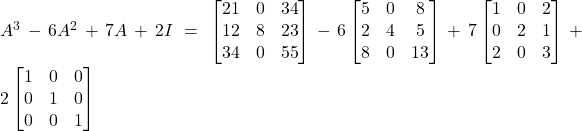



Hence![]() Proved
Proved
Question 17: If ![]() and
and ![]() , Find k so that
, Find k so that ![]() .
.
Solution: Since ![]()
![]()
![]()
![]()
![]()
![]()
Now ![]()
![]()
![]()
![]()
Ccmparing the corresponding element of two matrices
![]()
![]()
Question18: If ![]() and I is the indentity matrix of order 2 ,Show that
and I is the indentity matrix of order 2 ,Show that
![]()
Solution :
![]()
![]()
![]()
![]()
![]()
![]()
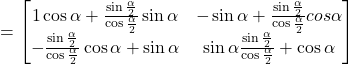
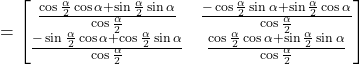
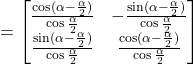

![]()
![]()
Question 19: A trust fund has ₹ 30,000 that must be invested in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication, determine how to divide ₹ 30,000 among the two types of bonds. If the trust fund must obtain an annual total interest of:
(a)₹ 1800 (b)₹ 2000
Solution: (a)![]()
![]()
![]()
![]()
![]()
Thus, in order to obtain an annual total interest of ₹1800, the trust fund should invest ₹15000 in the first bond and the remaining ₹15000 in the second bond.
(b) Let ₹ x be inested in
the first bond. Then the sum of money invested in the second bond will be ₹(30000-x)
Therefore, in order to obtain an annual total interest of ₹1800, we have
![]()
![]()
![]()
![]()
![]()
Thus, in order to obtain an annual total interest of ₹2000, the trust fund should invest ₹5000 in the first bond and the remaining ₹25000 in the second bond.
Question 20: The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are ₹80 , ₹ 60and ₹ 40 each respectively. Find the total amount the bookshop will receive from selling all the books using matrix algebra
Solution :books matrix =![]()
price matrix=![]()
Total cost =
![]()
![]()
![]()
Thus, the bookshop will receive ₹
20160 from the sale of all these books.
Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3 and p × k,
respectively. Choose the correct answer in Exercises 21 and 22.
Question 21: The restriction on n, k and p so that PY + WY will be defined are:
(A)k=3,p=n (B)k is arbitrary p=2
(C)p is arbitrary k=3 (D)k=2,p=3
Solution: Order of P=p×k
Order of Y=3×k
Order of PY= ![]()
Hence k=3
Order of W=![]()
Order of WY=![]()
order of PY + WY =![]()
It is possible if p=n
and k=3
hence option (A) is true
Queestion 22:If n = p, then the order of the matrix 7X – 5Z is:
(A) p × 2 (B) 2 × n (C) n × 3 (D) p × n
Solution: Order of matrix X= 2× n
Order of matrix = 2× p
Order of marix ![]() or
or ![]()
Hence the correct option is (B)