Multiple choice (Determinants)

Choose and write the correct option in the following question:(Class 12 determinants multiple choice question)
1.) ![]() , then x is equal to
, then x is equal to
(a) 6 (b) ±6
(c) -6 (d) 0
Answer:(b)
2.) The area of a triangle with vertices (-3, 0), (3, 0), and (0, k) is 9 sq. units. The value of k will be
(a) 9 (b) 3
(c) -9 (d) 6
Answer (b)
3.) If 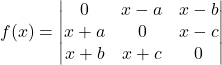 , then
, then
(a) f(a) = 0 (b) f(b) = 0
(c) f(0) = 0 (d) f(1) = 0
Answer (c)
4.) If 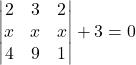 , then the value of x is
, then the value of x is
(a) 3 (b) 0
(c) -1 (d) 1
Answer (c)
5.) If ![]() denotes the cofactor of element
denotes the cofactor of element ![]() of the matrix
of the matrix 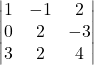 , then the value of
, then the value of ![]() is
is
(a) 5 (b) 24
(c) -24 (d) -5
Answer (a)
6.) If x = -4 is a root of 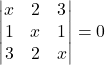 , then the sum of the other rwo roots is
, then the sum of the other rwo roots is
(a) 4 (b) -3
(c) 2 (d) 5
Answe (a)
7.) If for a matrix ![]() , then the value of α is
, then the value of α is
(a) ±3 (b) -3
(c) ±1 (d) 1
Answer (a)
8.) If 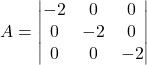 , then the value of
, then the value of ![]() is
is
(a) 64 (b) 16
(c) 0 (d) -8
Answer (a)
9.) If A is square matrix of order 3, such that ![]() , then
, then ![]() is equal to
is equal to
(a) 1 (b) 10
(c) 100 (d) 101
Answer (c)
10.) If ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) I
Answer (b)
11.) The sum of the products of elements of any row with the co-factors of corresponding elements equal to
(a) Cofactor sum (b) Value of the derminant
(c) 0 (d) Adjoint of matrix
Answer (b)
12.) The matrix 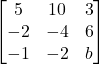 is singular matrix, if the value of b is
is singular matrix, if the value of b is
(a) -3 (b) 3
(c) 0 (d) Any real number
Answe (d)
13.) If x, y, z are non zero real numbers, then the inverse of matrix 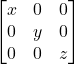 is
is
(a) 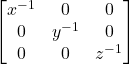
(b) 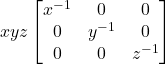
(c) 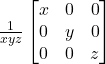
(d) 
Answer (a)
14.) If ![]() then the value of
then the value of ![]() is
is
(a) ![]()
(b) ![]()
(c) A’
(d) Zero matrix
Answer (a)
15.) The value of ![]() is
is
(a) ![]() (b)
(b) ![]()
(c) I (d) ![]()
Answer (a)
16.) If A is an invertible matrix of order 2, then ![]() is equal to
is equal to
(a) det A (b) ![]()
(c) 1 (d) 0
Answer (b)
17.) If A is singular matrix, then A(adj A) is
(a) Null matrix (b) Scalar matrix
(c) Identity matrix (d) None of these
Answer (a)
18.) Using matrix method to solve the following system of equations: 5x – 7y = 2, 7x – 5y = 3, value of x, y is
(a) x = 11/24, y = 1/24 (b) x = -11/24, y = 1/24
(c) x = 1, y = 1 (d) x = 10/24, y = 1/24
Answer (a)
19.) If A is square matrix of order 3×3 such that |A| = 2, then the value of ![]() is
is
(a) -16 (b) 16
(c) 0 (d) 2
Answer (b)
20.) If A and B are invertible matrices, then which of the following is NOT correct.
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
Answer (d)


