Question 5:- In a group of 50 scouts in a camp, 30 are well trained in first aid techniques while the remaining are well trained in hospitality but not in first aid. Two scouts are selected at random from the group. Find the probability distribution of number of selected scouts who are well trained in first aid . Find the mean of the distribution also.
Write one more value which is expected from a well trained scouts. [Foreign]
Solution:- X: Number of selected scouts who are well trained in first aid.
X can take values = 0, 1, 2.
S: Scouts well trained in first aid are selected. [Out of 50 scouts, 30 are well trained in first aid.]
![]()
![]()
![]()
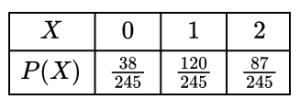
Henc, mean = Σ X.P(X)
![]()
![]()
Another value expected from a well trained scouts is brave/pure in thoughts and deeds.
Question 1:- The probabilities of two students A and B coming to the school in time are 3/7 and 5/7 respectively. Assuming that the events, ‘A coming in time’ and ‘B coming in time’ are independent, find the probability of only one of them coming to the school in time. [CBSE(AI) 2013]
Solution: for solution please click here
Question 2:- A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B wins the game if he gets a total of 10. If A starts the game, then find the probability that B wins. [CBSE Delhi 2016]
Solution: For solution please click here
Question 3:- A, B and C throw a pair of dice in that order alternately till one of them gets a total of 9 and wins the game . Find their respective probabilities of winning, if A starts first. [CBSE(East) 2016]
Solution: For solution please click here
Question 4:- The probability that A hits a target is 1/3 and the probability that B hits it is 2/5. If each one of A and B shoots at the target, what is the probability that [CBSE (F) 2009]
(i) The target is hit ? (ii) Exactly one of them hits the target ?
Solution: For solution please click here
Question 6:- A bag I contains 5 red and 4 white balls and a bag II contains 3 red and 3 white balls. Two balls are transferred from the bag I to the bag II and then one ball is drawn from the bag II. If the ball drawn from the bag II is red, then find the probability that one red and one white ball are transferred from the bag I to the bag II. [CBSE Sample paper 2016]
Solution: For solution please click here