Exercise 7.11

By using the properties of definite integrals, evaluate the integrals in Exercises 1 to 19.(Ex 7.11 integration ncert maths solution class 12)

Question 1: $\int_0^{\frac{\pi}{2}} \cos ^2 x d x$

Solution : Let $I=\int_0^{\frac{\pi}{2}} \cos ^2 x d x$

$I=\int_0^{\frac{\pi}{2}} \cos ^2\left(\frac{\pi}{2}-x\right) d x \quad\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$I=\int_0^{\frac{\pi}{2}} \sin ^2 x d x$

Adding (1) and (2), we have

$2 I=\int_0^{\frac{\pi}{2}}\left(\sin ^2 x+\cos ^2 x\right) d x$

$2 I=\int_0^{\frac{\pi}{2}} 1 d x$

$\Rightarrow 2 I=[x]_0^{\frac{\pi}{2}}$

$\Rightarrow 2 I=\frac{\pi}{2}$

$\Rightarrow I=\frac{\pi}{4}$

Question 2: $\int_0^{\frac{\pi}{2}} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x$

Solution: Let $I=\int_0^{\frac{\pi}{2}} \frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}} d x$

$\Rightarrow I=\int_0^{\frac{\pi}{2}} \frac{\sqrt{\sin \left(\frac{\pi}{2}-x\right)}}{\sqrt{\sin \left(\frac{\pi}{2}-x\right)}+\sqrt{\cos \left(\frac{\pi}{2}-x\right)}} d x \quad\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$I=\int_0^{\frac{\pi}{2}} \frac{\sqrt{\cos x}}{\sqrt{\cos x}+\sqrt{\sin x}} d x$

Adding (1) and (2), we have

$2 I=\int_0^{\frac{\pi}{2}}\left(\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}+\frac{\sqrt{\cos x}}{\sqrt{\cos x}+\sqrt{\sin x}}\right) d x$

$\Rightarrow 2 I=\int_0^{\frac{\pi}{2}}\left(\frac{\sqrt{\sin x}+\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}\right) d x$

$\Rightarrow 2 I=\int_0^{\frac{\pi}{2}} 1 d x$

$\Rightarrow 2 I=[x]_0^{\frac{\pi}{2}}$

$\Rightarrow 2 I=\frac{\pi}{2}$

$\Rightarrow I=\frac{\pi}{4}$

Question 3: $\int_0^{\frac{\pi}{2}} \frac{\sin ^{\frac{3}{2}} x}{\sin ^{\frac{3}{2}} x+\cos ^{\frac{3}{2}} x} d x$

Solution:Let $I=\int_0^{\frac{\pi}{2}} \frac{\sin ^{\frac{3}{2}} x}{\sin ^{\frac{3}{2}} x+\cos ^{\frac{3}{2}} x} d x--(i)$

$=\int_0^{\frac{\pi}{2}} \frac{\sin ^{\frac{3}{2}}\left(\frac{\pi}{2}-x\right)}{\sin ^{\frac{3}{2}}\left(\frac{\pi}{2}-x\right)+\cos ^{\frac{3}{2}}\left(\frac{\pi}{2}-x\right)} d x \quad\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$I=\int_0^{\frac{\pi}{2}} \frac{\cos ^{\frac{3}{2}} x}{\cos ^{\frac{3}{2}} x+\sin ^{\frac{3}{2}} x} d x--(ii)$

Adding (1) and (2), we have

$2 I=\int_0^{\frac{\pi}{2}} \frac{\sin ^{\frac{3}{2}} x+\cos ^{\frac{3}{2}} x}{\sin ^{\frac{3}{2}} x+\cos ^{\frac{3}{2}} x} d x \Rightarrow 2 I=\int_0^{\frac{\pi}{2}} 1 d x$

$\Rightarrow \quad I=[x]_0^{\frac{\pi}{2}} \Rightarrow 2 I=\frac{\pi}{2} \Rightarrow I=\frac{\pi}{4}$

Question4: $\int_0^{\frac{\pi}{2}} \frac{\cos ^5 x d x}{\sin ^5 x+\cos ^5 x} d x$

Solution: Let $I=\int_0^{\frac{\pi}{2}} \frac{\cos ^5 x d x}{\sin ^5 x+\cos ^5 x} d x---(i)$

$=\int_0^{\frac{\pi}{2}} \frac{\cos ^5\left(\frac{\pi}{2}-x\right) d x}{\sin ^5\left(\frac{\pi}{2}-x\right)+\cos ^5\left(\frac{\pi}{2}-x\right)} d x \quad\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$I=\int_0^{\frac{\pi}{2}} \frac{\sin ^5 x d x}{\cos ^5 x+\sin ^5 x} d x--(ii)$

$2 I=\int_0^{\frac{\pi}{2}} \frac{\sin ^5 x+\cos ^5 x}{\cos ^5 x+\sin ^5 x} d x$

$\Rightarrow 2 I=\int_0^{\frac{\pi}{2}} 1 d x$

$\Rightarrow 2 I=[x]_0^{\frac{\pi}{2}}$

$\Rightarrow 2 I=\frac{\pi}{2}$

$\Rightarrow I=\frac{\pi}{4}$

Question 5: $\int_{-5}^5|x+2| d x$

Solution: Let $I=\int_{-5}^5|x+2| d x--(i)$

$|x+2|=\begin{cases} -(x+2) & x<-2 \\ (x+2) & x\geq -2\end{cases}$

$I=\int_{-5}^{-2}-(x+2) d x+\int_{-2}^5(x+2) d x$

$\left[\text { Using property: } \int_a^b f(x)=\int_a^e f(x)+\int_e^b f(x)\right]$

$I=-\left[\frac{x^2}{2}+2 x\right]_{-5}^{-2}+\left[\frac{x^2}{2}+2 x\right]_{-2}^5$

$=-\left[\frac{(-2)^2}{2}+2(-2)-\frac{(-5)^2}{2}-2(-5)\right]+\left[\frac{(5)^2}{2}+2(5)-\frac{(2)^2}{2}+2(2)\right]$

$I=-\left[2-4-\frac{25}{2}+10\right]+\left[\frac{25}{2}+10-2+4\right]$

$=-2+4+\frac{25}{2}-10+\frac{25}{2}+10-2+4$

$=29$

Question 6: $\int_2^8|x-5| d x$

Solution: Let $I=\int_2^8|x-5| d x$

$|x-5|=\begin{cases} -(x-5) & x<5 \\ (x-5) & x\geq -5\end{cases}$

$I=\int_2^5-(x-5) d x+\int_2^8(x-5) d x$

$\left[\text { Using property: } \int_a^b f(x)=\int_a^e f(x)+\int_e^b f(x)\right]$

$I=-\left[\frac{x^2}{2}-5 x\right]_2^5+\left[\frac{x^2}{2}-5 x\right]_5^8$

$I=-\left[\frac{25}{2}-25-2+10\right]+\left[32-40-\frac{25}{2}+25\right]=9$

Question 7: $\int_0^1 x(1-x)^n d x$

Solution: Let $I=\int_0^1 x(1-x)^n d x$

$=\int_0^1(1-x)(1-(1-x))^n d x$

$\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$=\int_0^1(1-x)(x)^n d x=\int_0^1\left(x^n-x^{n+1}\right) d x=\left[\frac{x^{n+1}}{n+1}-\frac{x^{n+2}}{n+2}\right]_0^1$

$=\left[\frac{1}{n+1}-\frac{1}{n+2}\right]$

$=\frac{(n+2)-(n+1)}{(n+1)(n+2)}=\frac{1}{(n+1)(n+2)}$

Question 8: $\int_0^{\frac{\pi}{4}} \log (1+\tan x) d x$

Solution: Let $I=\int_0^{\frac{\pi}{4}} \log (1+\tan x) d x$

$=\int_0^{\frac{\pi}{4}} \log \left[1+\tan \left(\frac{\pi}{4}-x\right)\right] d x$

$\left[\right.$ Using property: $\left.\int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$I=\int_0^{\frac{\pi}{4}} \log \left[1+\frac{\tan \frac{\pi}{4}-\tan x}{1+\tan \frac{\pi}{4} \tan x}\right] d x$

$I=\int_0^{\frac{\pi}{4}} \log \left[1+\frac{1-\tan x}{1+\tan x}\right] d x$

$I=\int_0^{\frac{\pi}{4}} \log \frac{2}{(1+\tan x)} d x$

$=\int_0^{\frac{\pi}{4}} \log 2 d x-\int_0^{\frac{\pi}{4}} \log (1+\tan x) d x$

$\Rightarrow I=\int_0^{\frac{\pi}{4}} \log 2 d x-I$

$2 I=[x \log 2]_0^{\frac{\pi}{4}}$

$\Rightarrow 2 I=\frac{\pi}{4} \log 2$

$\Rightarrow I=\frac{\pi}{8} \log 2$

Question 9: $\int_0^2 x \sqrt{2-x} d x$

Soltuion: Let $I=\int_0^2(2-x) \sqrt{x} d x$

$\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$=\int_0^2\left[2 x^{\frac{1}{2}}-x^{\frac{3}{2}}\right] d x$

$=\left[2\left(\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right)-\left(\frac{x^{\frac{5}{2}}}{\frac{5}{2}}\right)\right]_0^1$

$=\left[\frac{4}{3} x^{\frac{3}{2}}-\frac{2}{5} x^{\frac{5}{2}}\right]_0^1$

$=\frac{4}{3}(2)^{\frac{3}{2}}-\frac{2}{5}(2)^{\frac{5}{2}}$

$=\frac{4 \times 2 \sqrt{2}}{3}-\frac{2}{5} \times 4 \sqrt{2}$

$=\frac{8 \sqrt{2}}{3}-\frac{8 \sqrt{2}}{5}$

$=\frac{40 \sqrt{2}-24 \sqrt{2}}{15}=\frac{16 \sqrt{2}}{15}$

Question 10: $\int_0^{\frac{\pi}{2}}(2 \log \sin x-\log \sin 2 x) d x$

Solution: Let $I=\int_0^{\frac{\pi}{2}}(2 \log \sin x-\log \sin 2 x) d x$

$=\int_0^{\frac{\pi}{2}}\{(2 \log \sin x-\log (2 \sin x \cos x)\} d x$

$=\int_0^{\frac{\pi}{2}}\{(2 \log \sin x-\log \sin x-\log \cos x-\log 2)\} d x$

$I=\int_0^{\frac{\pi}{2}}\{(\log \sin x-\log \cos x-\log 2)\} d x--(i)$

Using property, $\left\{\int_0^a f(x) d x=\int_0^a f(a-x) d x\right\}$ , we have

$I=\int_0^{\frac{\pi}{2}}\{(\log \cos x-\log \sin x-\log 2)\} d x$

Adding (1) and (2), we have

$2 I=\int_0^{\frac{\pi}{2}}(-\log 2-\log 2) d x$

$\Rightarrow 2 I=-2 \log 2 \int_0^{\frac{\pi}{2}} 1 d x$

$\Rightarrow I=-\log 2\left[\frac{\pi}{2}\right]$

$\Rightarrow I=\frac{\pi}{2}(-\log 2)$

$\Rightarrow I=-\frac{\pi}{2} \log 2$

Question 11: $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^2 x d x$

Solution: Let $I=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^2 x d x$

Here, $\sin ^2(-x)=(\sin (-x))^2=\sin ^2 x$ , therefore, $\sin ^2 x$ is an even function.

We know that if $f(x)$ is an even function, then $\int_{-a}^a f(x) d x=2 \int_0^a f(x) d x$

$I=2 \int_0^{\frac{\pi}{2}} \sin ^2 x d x$

$=2 \int_0^{\frac{\pi}{2}} \frac{1-\cos 2 x}{2} d x$

$=\int_0^{\frac{\pi}{2}}(1-\cos 2 x) d x$

$=\left[x-\frac{\sin 2 x}{2}\right]_0^{\frac{\pi}{2}}$

$=\frac{\pi}{2}-0=\frac{\pi}{2}$

Question 12: $\int_0^\pi \frac{x d x}{1+\sin x}$

Solution:- Let $I=\int_0^\pi \frac{x d x}{1+\sin x}$

$I=\int_0^\pi \frac{(\pi-x) d x}{1+\sin (\pi-x)} \quad \ldots(1)$

$I=\int_0^\pi \frac{(\pi-x) d x}{1+\sin x}--(ii)$

$\text { Adding } \left.\quad[1) \operatorname{and}(2), \text { we have property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$2 I=\int_0^\pi \frac{\pi d x}{1+\sin x}$

$\Rightarrow 2 I=\pi \int_0^\pi \frac{(1-\sin x) d x}{(1+\sin x)(1-\sin x)}$

$\Rightarrow 2 I=\pi \int_0^\pi \frac{1-\sin x}{\cos ^2 x} d x$

$2 I=\pi \int_0^\pi\left\{\sec ^2 x-\tan x \sec x\right\} d x$

$\Rightarrow 2 I=\pi[\tan x \sec x]_0^\pi$

$\Rightarrow 2 I=\pi[2] \Rightarrow I=\pi$

Question 13: $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^7 x d x$

Solution: Let $I=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^7 x d x$

Here, $\sin ^7(-x)=[(\sin (-x))]^7=(-\sin x)^2=-\sin ^7 x$ , therefore, $\sin ^7 x$ is an odd function.

We know that if $f(x)$ is an even function, then $\int_{-a}^a f(x) d x=0$

Therefore, $I=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^7 x d x=0$

Question 14: $\int_0^{2 \pi} \cos ^5 x d x$

Solution: Let $I=\int_0^{2 \pi} \cos ^5 x d x--(i)$

We know that,

$\int_0^{2 a} f(x) d x= \begin{cases}2 \int_0^a f(x) d x & \text { if } f(2 a-x)=f(x) \\ 0 & \text { if } f(2 a-x)=-f(x)\end{cases}$

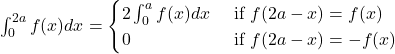
Here, $\quad \cos ^5(2 \pi-x)=\cos ^5 x$

$\therefore I=2 \int_0^\pi \cos ^5 x d x$

Now, $\quad \cos ^5(\pi-x)=-\cos ^5 x$

$\therefore I=2(0)=0$

Question 15: $\int_0^{\frac{\pi}{2}} \frac{\sin x-\cos x}{1+\sin x \cos x} d x$

Solution : Let $I=\int_0^{\frac{\pi}{2}} \frac{\sin x-\cos x}{1+\sin x \cos x} d x--(i)$

$\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$=\int_0^{\frac{\pi}{2}} \frac{\sin \left(\frac{\pi}{2}-x\right)-\cos \left(\frac{\pi}{2}-x\right)}{1+\sin \left(\frac{\pi}{2}-x\right) \cos \left(\frac{\pi}{2}-x\right)} d x \quad \text {.. (2) }$

$=\int_0^{\frac{\pi}{2}} \frac{\cos x-\sin x}{1+\sin x \cos x} d x$

Adding (1) and (2), we have

$2 I=\int_0^{\frac{\pi}{2}} \frac{0}{1+\sin x \cos x} d x=0$

$\Rightarrow I=0$

Question 16: $\int_0^\pi \log (1+\cos x) d x$

Solution : Let $I=\int_0^\pi \log (1+\cos x) d x--(i)$

$I =\int_0^\pi \log (1+\cos (\pi-x)) d x$

$\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$I =\int_0^\pi \log (1-\cos x) d x --ii$

Adding (1) and (2), we have

$2 I=\int_0^\pi\{\log (1+\cos x)+\log (1-\cos x)\} d x$

$=\int_0^\pi \log \left(1-\cos ^2 x\right) d x$

$2 I=\int_0^\pi \log \left(\sin ^2 x\right) d x=2 \int_0^\pi \log (\sin x) d x$

$\Rightarrow I=\int_0^\pi \log (\sin x) d x$

We know that,

$\int_0^{2 a} f(x) d x= \begin{cases}2 \int_0^a f(x) d x & \text { if } f(2 a-x)=f(x) \\ 0 & \text { if } f(2 a-x)=-f(x)\end{cases}$

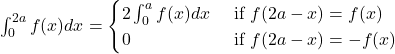
Here, $\sin (\pi-x)=\sin x$

$I=2 \int_0^{\frac{\pi}{2}} \log \sin x d x--(iii)$

$I=\int_0^{\frac{\pi}{2}} \log \sin \left(\frac{\pi}{2}-x\right) d x$

$=2 \int_0^{\frac{\pi}{2}} \log \cos x d x--(iv)$

Adding (4) and (5), we have

$2 I=2 \int_0^{\frac{\pi}{2}}(\log \sin x+\log \cos x) d x$

$\Rightarrow I=\int_0^{\frac{\pi}{2}}(\log \sin x+\log \cos x+\log 2-\log 2) d x$

$\Rightarrow I=\int_0^{\frac{\pi}{2}}(\log 2 \sin x \cos x-\log 2) d x$

$\Rightarrow I=\int_0^{\frac{\pi}{2}} \log 2 \sin x \cos x d x-\int_0^{\frac{\pi}{2}} \log 2 d x$

$\Rightarrow I=\int_0^{\frac{\pi}{2}} \log \sin 2 x d x-\log 2[x] \frac{\pi}{2}=\int_0^{\frac{\pi}{2}} \log \sin 2 x d x-\frac{\pi}{2} \log 2$

Let $2 x=t \quad \Rightarrow 2 d x=d t$

Question 17: $\int_0^a \frac{\sqrt{x}}{\sqrt{x}+\sqrt{a-x}} d x$

Solution : Let $I=\int_0^a \frac{\sqrt{x}}{\sqrt{x}+\sqrt{a-x}} d x--(i)$

$\left[\right.$ Using property: $\left.\int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$ , we have

$I=\int_0^a \frac{\sqrt{a-x}}{\sqrt{a-x}+\sqrt{x}} d x--(ii)$

Adding (1) and (2), we have

$2 I=\int_0^a \frac{\sqrt{x}+\sqrt{a-x}}{\sqrt{x}+\sqrt{a-x}} d x$

$\Rightarrow 2 I=\int_0^a 1 d x$

$\Rightarrow 2 I=[x]_0^a$

$\Rightarrow 2 I=a$

$\Rightarrow I=\frac{a}{2}$

Question 18: $\int_0^4|x-1| d x$

Solution : $I=\int_0^4|x-1| d x$

$|x-1| = \begin{cases} -(x-1) & x<1 \\(x-1) & x\geq 1\end{cases}$

$I=\int_0^1-(x-1) d x+\int_1^4(x-1) d x$

$\left[\text { Using property: } \int_a^b f(x)=\int_a^e f(x)+\int_e^b f(x)\right]$

$=\left[x-\frac{x^2}{2}\right]_0^1+\left[\frac{x^2}{2}-x\right]_1^4$

$=1-\frac{1}{2}+\frac{(4)^2}{2}-4-\frac{1}{2}+1$

$=1-\frac{1}{2}+8-4-\frac{1}{2}+1=5$

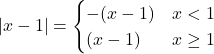
Question 19: Show that $\int_0^a f(x) g(x) d x=2 \int_0^a f(x) d x, \quad$ if $f$ and $g$ are defined as $f(x)=f(a-x)$ and $g(x)+g(a-x)=4$

Solution : Let $I =\int_0^a f(x) g(x) d x$

$I =\int_0^a f(a-x) g(a-x) d x$

$\left[\text { Using property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$

$I =\int_0^a f(x) g(a-x) d x$

Adding (1) and (2), we have

$2 I=\int_0^a\{f(x) g(x)+f(x) g(a-x)\} d x$

$\Rightarrow 2 I=\int_0^a\{f(x)\{g(x)+g(a-x)\}\} d x$

$\Rightarrow 2 I=\int_0^a f(x) \times 4 d x \quad \text { [Given that: } g(x)+g(a-x)=4 \text { ] }$

$\Rightarrow I=2 \int_0^a f(x) d x$

Question 20: The value of $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(x^3 d x+x \cos x+\tan ^5 x+1\right) d x$ is

(A) 0

(B) 2

(C) $\pi$

(D) 1

Solution : The correct answer is (C)

Let $I=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(x^3+x \cos x+\tan ^5 x+1\right) d x$

$I=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} x^3 d x+\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} x \cos x d x+\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \tan ^5 x d x+\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} 1 d x$

We know that,
$\int_{-a}^a f(x) d x= \begin{cases}2 \int_0^a f(x) d x & \text { if } f(x) \text { is an even function } \\ 0 & \text { if } f(x) \text { is an odd function }\end{cases}$

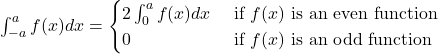
Therefore,

$I=0+0+0+2 \int_0^{\frac{\pi}{2}} 1 d x$

$=2[x]_0^{\frac{\pi}{2}}=\frac{2 \pi}{2}=\pi$

Hence, the correct answer is (C).

Question 21: The value of $\int_0^{\frac{\pi}{2}} \log \left(\frac{4+3 \sin x}{4+3 \cos x}\right) d x$ is

(A) 2

(B) $\frac{3}{4}$

(C) 0

(D) $-2$

Solution: The correct answer is (C)

Let $I=\int_0^{\frac{\pi}{2}} \log \left(\frac{4+3 \sin x}{4+3 \cos x}\right) d x \quad \ldots(1)$

$I=\int_0^{\frac{\pi}{2}} \log \left(\frac{4+3 \sin \left(\frac{\pi}{2}-x\right)}{4+3 \cos \left(\frac{\pi}{2}-x\right)}\right) d x \quad\left[\operatorname{sing} \text { property: } \int_0^a f(x) d x=\int_0^a f(a-x) d x\right]$