Case study Chapter 8 (Application of Integral)
Case study 1: Read the following and answer the question.(Case study application of integral 1)
Nowadays, almost every boat has a triangular sail. By using a triangular sail design it has become possible to travel against the wind using a technique known as tacking. Tacking allows the boat to travel forward with r
triangular sail on the walls and three edges(lines) at the triangular sail are given by the equation x = 0, y = 0 and y + 2x – 4 = 0 respectively.

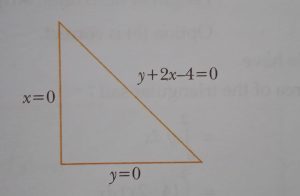
(i) Point of intersection of the edges(lines) y + 2x – 4 = 0 and y = 0
(a) (4, 0) (b) (0, 4)
(c) (2, 0) (d) (0, 2)
(ii) Length of each vertical strip of the sail is given by
(a) -2x + 4 (b) y + 4
(c) x – 4 (d) y – 4
(iii) The point of intersection of the edges(lines) of the sail given by the equation y + 2x – 4 = 0 and x = 0 is
(a) (2, 0) (b) (4, 0)
(c) (0, 2) (d) (0, 4)
(iv) Length of each horizontal strip of the sail is given by
(a) (4 – y) (b) 1/2(4 – y)
(c) 1/2(4 – x) (d) (4 – 2x)
(v) The area of triangular sail is ( in square units)
(a) 4 (b) 2
(c) 8 (d) 16
Solution: (i) Answer (c)
Given equation, y + 2x – 4 = 0
x = 2
Point of intersection is (2, 0)
(ii) answer (a)
We have y + 2x – 4 = 0
y = 4 – 2x
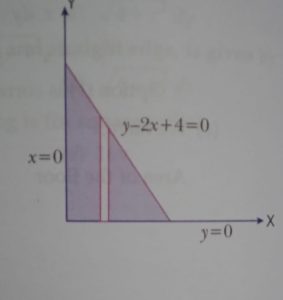
Length of vertical strip is given by
y = 4 – 2x
i.e. -2x + 4
(iii) Answer (d)
y + 2x – 4 = 0 —(i)
and x = 0 —(ii)
From equation (i) and (ii), we have
y + 0 – 4 = 0
y = 4
Point of intersection is (0, 4)
(iv) Answer (b)
We have

y + 2x – 4 = 0
2x = 4 – y
x = 1/2(4 – y)
(v) Answer (a)
we have
Area of triangular sail ![]()
![]()
![]()
![]() sq. units
sq. units
Some other Case study problem
Case study 2: Read the following and answer the question(Case study application of integral 2)
An architect designs a building whose lift (elevator ) is from outside of the building attached to the walls. The floor (base ) of the lift (elevator) is in semicircular shape. The floor of the elevator (lift) whose circular edge is given by the equation ![]() and the straight edge(line) is given by the equation y = 0.
and the straight edge(line) is given by the equation y = 0.

Solution: For solution click here
Case study 3: Read the following and answer the question(Case study application of integral 3)
A student designs an open air Honeybee nest on the branch of a tree, whose plane figure is parabolic and the branch of tree is given by a straight line.

Solution: For solution click here
Case study 4: Read the following and answer the question
A boy design a pizza by cutting it with a knife on a card board. If pizza is circular in shape which is represented by the
equation ![]() and edge of knife represents a straight line given by
and edge of knife represents a straight line given by ![]() .
.

Solution: For solution click here
Case study 5:-A farmer has a triangular shaped field. His, son a science student observes the triangular field has three edges and can be drawn on a plain paper with three lines given by its equations.(Case study application of integral 5)

Based on the above information answer the following question:
(i) Find the area of the shaped region in the figure shown below.
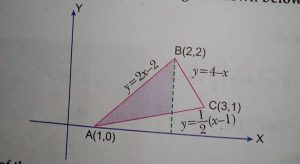
(ii) Find the area of the triangle ΔABC.
Solution: For solution click here


