EXERCISE 1.5
(Ex 1.5 sets ncert maths solution class 11)
1. Let U = {1, 2, 3; 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8}, and C = {3, 4, 5, 6}. Find
(i) A’
(ii) B’
(iii) (A U C)’
(iv) (A U B)’
(v) (A’)’
(vi) (B – C)’
Solution: It is given that
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 4}
B = {2, 4, 6, 8}
C = {3, 4, 5, 6}
(i) A’ = {5, 6, 7, 8, 9}
(ii) B’ = {1, 3, 5, 7, 9}
(iii) A U C = {1, 2, 3, 4, 5, 6}
So, we get
(A U C)’ = {7, 8, 9}
(iv) A U B = {1, 2, 3, 4, 6, 8}
So, we get
(A U B)’ = {5, 7, 9}
(v) (A’)’ = A = {1, 2, 3, 4}
(vi) B – C = {2, 8}
So, we get
(B – C)’ = {1, 3, 4, 5, 6, 7, 9}
2. If U = {a, b, c, d, e, f, g, h}, find the complements of the following sets:
(i) A = {a, b, c}
(ii) B = {d, e, f, g}
(iii) C = {a, c, e, g}
(iv) D = {f, g, h, a}
Solution: (i) A = {a, b, c}
A’ = {d, e, f, g, h}
(ii) B = {d, e, f, g}
B’ = {a, b, c, h}
(iii) C = {a, c, e, g}
C’ = {b, d, f, h}
(iv) D = {f, g, h, a}
D’ = {b, c, d, e}
3. Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {x: x is an even natural number}
(ii) {x: x is an odd natural number}
(iii) {x: x is a positive multiple of 3}
(iv) {x: x is a prime number}
(v) {x: x is a natural number divisible by 3 and 5}
(vi) {x: x is a perfect square}
(vii) {x: x is perfect cube}
(viii) {x: x + 5 = 8}
(ix) {x: 2x + 5 = 9}
(x) {x: x ≥ 7}
(xi) {x: x ∈ N and 2x + 1 > 10}
Solution: We know that
U = N: Set of natural numbers
(i) Let A = {x: x is an even natural number}
⇒A’ = {x: x is an odd natural number}={1, 3, 5, 7, 9 . . . }
(ii) Let B = {x: x is an odd natural number}
⇒ B’ = {x: x is an even natural number} ={2, 4, 6, . …}
(iii) Let C = {x: x is a positive multiple of 3}
⇒ C’ = {x: x ∈ N and x is not a multiple of 3}
(iv) Let D = {x: x is a prime number}
⇒ D’ = {x: x is a positive composite number and x = 1}
(v) Let E = {x: x is a natural number divisible by 3 and 5}
⇒ E’ = {x: x is a natural number that is not divisible by 3 or 5}
(vi) Let F = {x: x is a perfect square}
⇒ F’ = {x: x ∈ N and x is not a perfect square}
(vii) Let G= {x: x is a perfect cube}
⇒ G’ = {x: x ∈ N and x is not a perfect cube}
(viii) Let H = {x: x + 5 = 8}
⇒ H’ = {x: x ∈ N and x ≠ 3}={1, 2, 4 , 5 , 6 . . . }
(ix)Let I = {x: 2x + 5 = 9}
⇒ I’ = {x: x ∈ N and x ≠ 2}
(x) Let J = {x: x ≥ 7}
⇒ J’ = {x: x ∈ N and x < 7} ={1, 2, 3, 4, 5, 6}
(xi) Let K = {x: x ∈ N and 2x + 1 > 10}
⇒ K’ = {x: x ∈ N and x ≤ 9/2}
4. If U = {1, 2, 3, 4, 5,6,7,8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that
(i) (A U B)’ = A’ ∩ B’
(ii) (A ∩ B)’ = A’ U B’
Solution: It is given that
U = {1, 2, 3, 4, 5,6,7,8, 9}
A = {2, 4, 6, 8}
B = {2, 3, 5, 7}
(i) (A U B)’ = {2, 3, 4, 5, 6, 7, 8}’ = {1, 9}
A’ ∩ B’ = {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9} = {1, 9}
Therefore, (A U B)’ = A’ ∩ B’.
(ii) (A ∩ B)’ = {2}’ = {1, 3, 4, 5, 6, 7, 8, 9}
A’ U B’ = {1, 3, 5, 7, 9} U {1, 4, 6, 8, 9} = {1, 3, 4, 5, 6, 7, 8, 9}
Therefore, (A ∩ B)’ = A’ U B’.
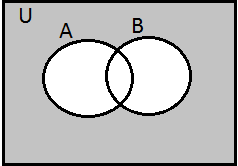
5. Draw an appropriate Venn diagram for each of the following:
(i) (A U B)’
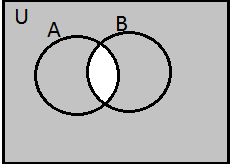
(ii) A’ ∩ B’
(iii) (A ∩ B)’
(iv) A’ U B’
Solution: (i) (A U B)’
(ii) A’ ∩ B’

(iii) (A ∩ B)’
(iv) A’ U B’

6. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A’?
Solution: A’ is the set of all equilateral triangles.
7. Fill in the blanks to make each of the following a true statement.
(i) A U A’ = ……..
(ii) Φ′ ∩ A = …….
(iii) A ∩ A’ = …….
(iv) U’ ∩ A = …….
Solution: (i) A U A’ = U
(ii) Φ′ ∩ A = U ∩ A = A
Φ′ ∩ A = A
(iii) A ∩ A’ = Φ
(iv) U’ ∩ A = Φ ∩ A = Φ
U’ ∩ A = Φ
https://gmath.in/ex-1-4-sets-ncert-maths-solution-class-11/