Chapter 5 Miscellaneous (differentiation )
Differentiate w.r.t. x the function in Exercises 1 to 11.(Class 12 ncert solution math chapter 5 miscellaneous)
Question 1: ![]()
Solution: Let ![]()
Differentiate with respect to x
![]()
![]()
![]()
![]()
Question 2: ![]()
Solution: Let ![]()
Differentiate with respect to x
![]()
![]()
![]()
![]()
![]()
Question 3: ![]()
Solution: Let ![]()
Taking ‘log’ both side
![]()
![]()
![]()
![]()
![]()
![]()
Question 4: ![]()
Solution: Let ![]()
Differentiate with respect to x
![]()
![]()
![]()
![]()
![]()
![]()
Question 5: ![]()
Solution : Let ![]()
Differentiate with respect to x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question6: ![]()
Solution: Let ![]()
Then,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore from equation (i)
![]()
![]()
Differentiate with respect to x
![]()
Question 7: ![]()
Solution: Let ![]()
Taking log both side, we obtain
![]()
![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
![]()
![]()
Question 8: ![]() , for some constant
, for some constant ![]() and
and ![]() .
.
Solution: Let ![]()
Using chain rule, we get
![]()
![]()
![]()
![]()
Question 9: ![]()
Solution: Let ![]()
Taking log on both the sides, we obtain
![]()
![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()

![]()
![]()
Question 10: Differentiate with respect to ![]() the function
the function ![]() , for some fixed
, for some fixed ![]() and
and ![]() .
.
Solution: Let ![]()
Also, let ![]() and
and ![]()
Therefore,
![]()
![]()
Now, ![]()
Taking logarithm on both the sides, we obtain
![]()
![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
Now, ![]()
Hence,
![]()
![]()
Now, ![]()
Taking logarithm on both the sides, we obtain
![]()
![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
Now, ![]()
Since ![]() is constant,
is constant, ![]() is also a constant.
is also a constant.
Hence,
![]()
From (1), (2), (3), (4) and (5), we obtain
![]()
![]()
Question 11: ![]() , for
, for ![]() .
.
Solution: Let ![]()
Also, let ![]() and
and ![]() Therefore,
Therefore,
![]()
![]()
Now, ![]() Taking logarithm on both the sides, we obtain
Taking logarithm on both the sides, we obtain
![]()
![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
Now, ![]()
Taking logarithm on both the sides, we obtain
![]()
![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
![]()
From (1), (2), and (3), we obtain
![]()
Question 12: Find ![]() , if
, if ![]()
Solution: The given function is ![]()
Hence,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore,
![]()
![]()
![]()
Question 13: Find ![]() , if
, if ![]() .
.
Solution: The given function is ![]()
Let ![]()
Let ![]()
![]()
![]()
![]()
Hence,
From (i)
![]()
Differentiate with respect to x
![]()
Question 14: If ![]() for
for ![]() , prove that
, prove that ![]() .
.
Solution:The given function is ![]()
![]()
Squaring both sides, we obtain
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
Hence proved.
Question 15:If ![]() for
for ![]() , prove that
, prove that ![Rendered by QuickLaTeX.com \frac{\left[1+\left(\frac{d y}{d x}\right)^2\right]^{\frac{3}{2}}}{\frac{d^2 y}{d x^2}}](https://gmath.in/wp-content/ql-cache/quicklatex.com-e1f31549baa567a786016a8134f9f076_l3.png)
is a constant independent of ![]() and
and ![]() .
.
Solution:The given function is ![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
![]()
Therefore,
![]()
![]()
![]()
![Rendered by QuickLaTeX.com =-\left[\frac{(y-b)-(x-a) \cdot\left\{\frac{-(x-a)}{y-b}\right\}}{(y-b)^2}\right] \quad[\text { Using (1)] }](https://gmath.in/wp-content/ql-cache/quicklatex.com-e8f67880e4ecbe253685e741ca45b32e_l3.png)
![]()
Hence,
![]()
![Rendered by QuickLaTeX.com =\frac{\left[\frac{(y-b)^2+(x-a)^2}{(y-b)^2}\right]^{\frac{3}{2}}}{-\left[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}\right]}](https://gmath.in/wp-content/ql-cache/quicklatex.com-33cd739de058b0d5a322ef688965a6c4_l3.png)
![Rendered by QuickLaTeX.com =\frac{\left[\frac{c^2}{(y-b)^2}\right]^{\frac{3}{2}}}{-\frac{c^2}{(y-b)^3}}](https://gmath.in/wp-content/ql-cache/quicklatex.com-16d9f09a9c4c670b112040e0e4f4028a_l3.png)
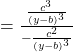
![]()
![]() is a constant and is independent of
is a constant and is independent of ![]() and
and ![]() .
.
Hence proved.
Question 16: If ![]() with
with ![]() , prove that
, prove that ![]() .
.
Solution: The given function is ![]()
Therefore,
![]()
![]()
![]()
![]()
Since, ![]()
![]()
Then, equation (1) becomes,
![]()
![]()
![]()
![]()
Hence proved.
Question 17: If ![]() and
and ![]() , find
, find ![]() .
.
Solution: The given function is ![]() and
and ![]() Therefore,
Therefore,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 18: If ![]() , show that
, show that ![]() exists for all real
exists for all real ![]() , and find it.
, and find it.
Solution: It is known that ![]()
Therefore, when ![]()
In this case, ![]() and hence,
and hence, ![]()
When ![]()
In this case, ![]() and hence,
and hence, ![]()
Thus, for ![]() exists for all real
exists for all real ![]() and is given by,
and is given by,
![]()
Question 19: Using mathematical induction prove that ![]() for all positive integers
for all positive integers ![]() .
.
Solution:To prove: ![]() for all positive integers
for all positive integers ![]() .
.
For ![]() ,
,
![]()
Therefore, ![]() is true for
is true for ![]() .
.
Let ![]() is true for some positive integer
is true for some positive integer ![]() .
.
That is, ![]()
It has to be proved that ![]() is also true.
is also true.
![]()
Taking, L.H.S.
![]()
![]()
![]()
![]()
![]()
![]()
Thus, ![]() is true whenever
is true whenever ![]() is true.
is true.
Therefore, by the principle of mathematical induction, the statement ![]() is true for every positive integer
is true for every positive integer ![]() .
.
Hence, proved.
Question 20: Using the fact that ![]() and the differentiation, obtain the sum formula for cosines.
and the differentiation, obtain the sum formula for cosines.
Solution: Given, ![]()
Differentiating both sides with respect to ![]() , we obtain
, we obtain
![]()
![]()
![]()
![]()
![]()
Question 21: Does there exist a function which is continuous everywhere but not differentiable at exactly two points? Justify your answer?
Solution: Consider, 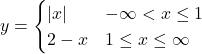
It can be seen from the above graph that the given function is continuous everywhere but not differentiable at exactly two points which are 0 and 1.
Question 22: 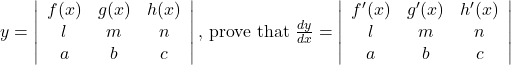
Solution: 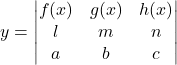
Differentiate with respect to x
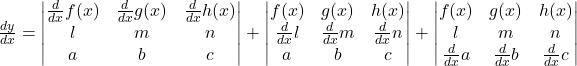
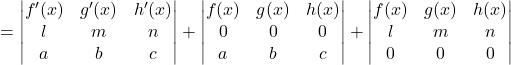
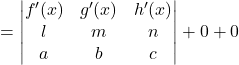
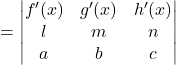
Hence proved
Question 23: If ![]() Show that
Show that ![]()
Solution: ![]()
Differentiate with respect to x
![]()
![]()
![]()
Multiply by ![]() both side
both side
![]()
![]()
Squaring both side
![]()
![]()
Again differentiate with respect to x
![]()
![]()
Divide by ![]() both side
both side
![]()
![]()