Chapter 6 : Triangles

Class 10 Case based problem of Chapter 6 Triangles 1

Case Stuydy :1

Peter, who is 1.6 m tall, is standing near a lamp post one day. He observes his shadow and also the shadow of the lamp post on the ground. He wanted to compare the length of his shadow with the shadow of the taller lamp post at the same time of the day. As he has an interest in geometry, he tries to relate the concepts in daily life. He find the length of his shadow CE to be 2.0 m, while the length of shadow of the lamp post AE was 6.0 m.

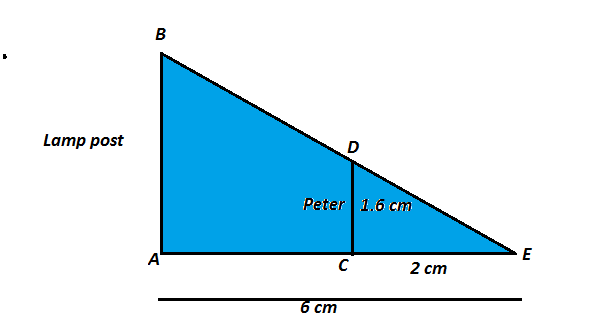
On the basis of the above information, answer the following question:

(A) Select the correct statement from the statements given below:

(a) Triangles ABE and CDE are congruent by AA criteria.

(b) Triangle ABE and CDE are similar by AA criteria.

(d) Triangles ABE and CDE are neither similar nor congruent.

(B) Find the length of the lamp post AB.

(C) Find the ratio of the sides DE and BD.

(D) In the given figure, DE||BC and $\frac{AD}{DB}=\frac{3}{5}$ . If AC = 4.8 cm, then AE is:

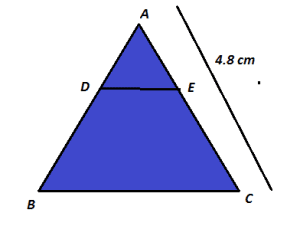
(a) 1.8 cm (b) 2.8 cm

Solution:

(A) Answer (b) Triangles ABE and CDE are congruent by AA criteria.

Explanation: In ΔABE and ΔCDE

∠A = ∠C = 90 degree

And ∠E is common in both triangles

Thus the ΔABE and ΔCDE are similar by AA criteria.

(B) From question (A) ΔABE and ΔCDE are similar by AA criteria

AE = 6 cm, CE = 2 cm and CD = 1.6 cm

Therefore, $\dfrac{AB}{CD}=\dfrac{AE}{CE}$

$\Rightarrow \dfrac{AB}{1.6}=\dfrac{6}{2}$

AB = 4.8

Hence the length of the lamppost AB = 4.8 m

(C) Since CD is parallel to AB

So, $\dfrac{CE}{AC}=\dfrac{DE}{BD}$ by Basic Proportionality Theorem

$\Rightarrow \dfrac{CE}{AE-CE}=\dfrac{DE}{BD}$

$\Rightarrow \dfrac{2}{6-2}=\dfrac{DE}{BD}$

$\Rightarrow \dfrac{1}{2}=\dfrac{DE}{BD}$

$\Rightarrow \dfrac{DE}{BD} = \dfrac{1}{2}$

Hence, the ratio of sides DE and BD = 1:2

(D) Answer (a) 1.8 cm

Explanation: Let AE = x cm,

Then, EC = (4.8 – x) cm.

As, DE||BC therefore, using BPT, we get

$\dfrac{AD}{DB}=\dfrac{AE}{EC}$

$\Rightarrow \dfrac{3}{5}=\dfrac{x}{4.8 - x}$

$\Rightarrow 3(4.8-x) = 5x$

$\Rightarrow 14.4 - 3x = 5x$

$\Rightarrow 8x = 14.4$

$\Rightarrow x = 1.8$ cm

Case study :2

While driving through the hils, Sneha observed a bridge in the shape of trapezium with the diagonals AC and BD intersecting each other at the point O.

(A) Which of the following statement is true regarding similarity of triangles formed ?

(a) ΔBOC ∼ ΔAOD by SAS similarity crriterion

(b) ΔAOB ∼ ΔCOD by AA similarity crriterion

(d) ΔAOB ∼ ΔDOC by SSS similarity crriterion

(B) ABCD is a trapezium in which AB||DC and P and Q are points on AD and BC, respectively such that PQ||DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, then the length of side AD.

(C) In a trapezium PQRS , PQ||SR. The diagonals PR and QS intersect at O. If OP = 3 cm, OR = 2 cm and OS = 4 cm, then find the length of side OQ.

(D) In the given figure, AB||DC and diagonals AC and BD intersects at O. If OA = 3x – 1 and OB = 2x + 1, OC = 5x – 3 and OD = 6x – 5, then, the value of x is:

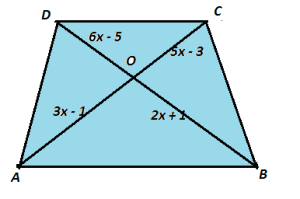
(a) 1 (b) 6

Solution:

(A) Answer (c) ΔBOC ∼ ΔDOA by AA similarity criterion

Explanation: Since, ABCD is a trapezium,

So BC||AD

∴ ∠CBO = ∠ADO

As they form a pair of alternate interior angles.

Also, ∠BOC = ∠DOA

[Vertically opposite angles]

Therefore, ΔBOC ∼ ΔDOA by AA similarity criterion.

(B) Consider the figure below :

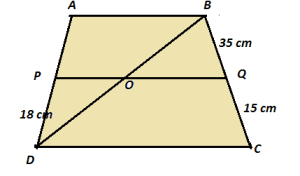
Join BD

As PQ||DC and AB||DC, we can say that PQ||AB

Applying Basic Proportionality theorem in ΔABD, we get

$\frac{AP}{DP}=\frac{BO}{OD}$ …….(i)

Similarly, in ΔBDC, we get

$\frac{BQ}{QC}=\frac{OB}{OD}$ ……..(ii)

From equation (i) and (ii), we get

$\frac{BQ}{QC}=\frac{AP}{DP}$

$\Rightarrow \frac{35}{15}=\frac{AP}{18}$

$\Rightarrow AP = \frac{35\times 18}{15}=42$

Now, AD = AP + PD

= 42 + 18 = 60 cm.

(C)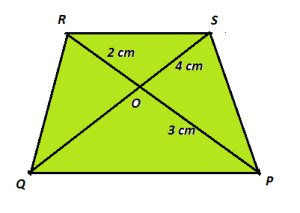

As PQ||SR, The triangles ΔPOQ and ΔROS are similar by AA similarity criteria as ∠QPO = ∠SRO( Alternate Interior Angles) and ∠POQ= ∠ROS(Vertically opposite angles).

Now as ΔPOQ ∼ ΔROS

∴ $\frac{OP}{OQ}=\frac{OR}{OS}$