Chapter 3 ( Miscellaneous)
class 12 maths chapter 3 Miscellaneous solution
Question 1: Let ,![]() show that ,
show that , ![]() where I is the identity matrix of order 2 and
where I is the identity matrix of order 2 and![]() .
.
Solution: It is given that ![]()
![]()
![]()
![]()
LHS.
![]()
RHS.
![]()
![]()
![]()
![]()
Since,
![]()
Hence,
![]()
We shall prove the result by using the principle of mathematical induction.
For n=1, we have:
P(1):![]()
![]()
Therefore, the result is true for n=1 .
Let the result be true for ![]()
That is :
P(k):![]()
Now, we have to prove that the result is true for ![]()
Consider,
![]()
LHS.
![]()
![]()
![]()
![]()
![]()
Therefore, the result is true for ![]()
Question 2: If  ,prove that
,prove that 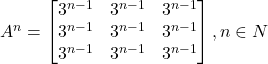
Solution: It is given that 
We shall prove the result by using the principle of mathematical induction.
Let the result be true for ![]() .
.
Now, we have:
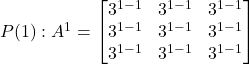
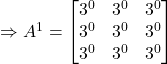
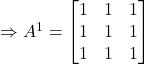
Therefore, the result is true for n=1.
Let the result be true for ![]() .
.
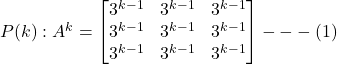
Now, we have to prove that the result is true for ![]() .
.
Since,
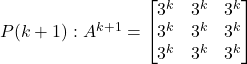
![]()
![]()
![Rendered by QuickLaTeX.com =\begin{bmatrix}3^{k-1}&3^{k-1}&3^{k-1}\\3^{k-1}&3^{k-1}&3^{k-1}\\3^{k-1}&3^{k-1}&3^{k-1}\end{bmatrix}\begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix}-----[From (1)]](https://gmath.in/wp-content/ql-cache/quicklatex.com-3c0938cbde528f4cd60c8ac511894de0_l3.png)
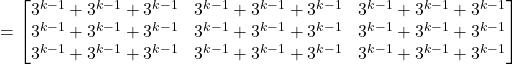
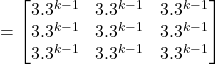

![]()
Therefore, the result is true for ![]() .
.
Question 3: If ![]() ,prove that
,prove that ![]() ,where is any positive integer.
,where is any positive integer.
Solution: It is given that ![]()
We shall prove the result by using the principle of mathematical induction.
For n=1 , we have:
![]()
![]()
![]()
Therefore, the result is true for ![]()
Let the result be true for n=k .
![]()
Now, we have to prove that the result is true for ![]() .
.
Since,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence,
![]()
Therefore, the result is true for ![]()
Question 4: If ![]() and
and![]() are symmetric matrices, prove that
are symmetric matrices, prove that![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Solution: It is given that![]() and
and![]() are symmetric matrices.
are symmetric matrices.
Therefore, we have:
![]() and
and ![]()
Now,
![]()
![]()
![]()
![]()
Hence,
![]()
Thus, ![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Question 5: Show that the matrix ![]() is symmetric or skew symmetric according as
is symmetric or skew symmetric according as ![]() is symmetric orskew symmetric.
is symmetric orskew symmetric.
Solution: We suppose that![]() is a symmetric matrix, then
is a symmetric matrix, then
![]()
Consider,
![]()
![]()
![]()
![]()
![]()
Therefore,
![]()
Thus, if ![]() is symmetric matrix, then
is symmetric matrix, then![]() is a symmetric matrix.
is a symmetric matrix.
Now, we suppose that ![]() is a skew symmetric matrix, then
is a skew symmetric matrix, then
![]()
Consider,
![]()
![]()
![]()
![]()
![]()
![]()
Therefore
![]()
Thus, if ![]() is a skew symmetric matrix, then
is a skew symmetric matrix, then ![]() is a skew symmetric matrix.
is a skew symmetric matrix.
Hence, if![]() is symmetric or skew symmetric matrix, then
is symmetric or skew symmetric matrix, then ![]() is symmetric or skew
is symmetric or skew
symmetric accordingly.
Question 6: Find the values of ![]() if the matrix
if the matrix satisfy the equation
satisfy the equation ![]()
Solution: It is given that 
Therefore,
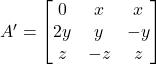
Now,
![]()
Hence,
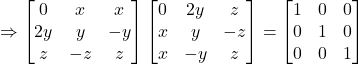
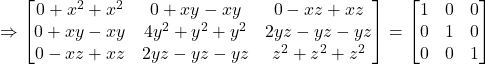

On comparing the corresponding elements, we have:
![]()
![]()
![]()
![]()
![]()
![]()
Hence,
![]() and
and ![]()
Question 7:For what values of x: ?
?
Solution: We have:

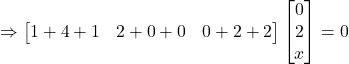
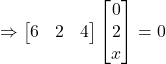
![]()
![]()
![]()
![]()
Thus, the required value of ![]() .
.
Question 8: If ![]() , show that
, show that ![]()
Solution : It is given that ![]()
Therefore,
![]()
![]()
![]()
![]()
Now,
![]()
![]()
![]()
![]()
![]()
![]()
Thus,![]()
Question 9: Find , if 
Solution: 
Hence,

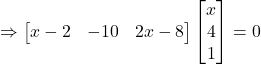
![]()
![]()
![]()
![]()
Question 10: A manufacturer produces three products ![]() which he sells in two markets. Annual sales are
which he sells in two markets. Annual sales are
indicated below:
Market Products
product x y z
I 10000 2000 18000
II 6000 20000 8000
(a) If unit sale prices of ![]() and
and ![]() are ₹ 2.50 ,₹ 1.50and₹ 1.00, respectively, find the total
are ₹ 2.50 ,₹ 1.50and₹ 1.00, respectively, find the total
revenue in each market with the help of matrix algebra.
(b) If the unit costs of the above three commodities are ₹2 , ₹1 and 50paise respectively.
Find the gross profit.
Solution: (a) The unit sale prices of ![]() and
and ![]() are ₹2.50 , ₹1.50 and ₹ 1.00respectively.
are ₹2.50 , ₹1.50 and ₹ 1.00respectively.
Consequently, the total revenue in market I can be represented in the form of a matrix as:
Product matrix:![]()
Sale price matirx: ![]()
The total revenue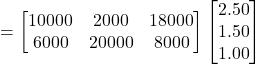
![]()
![]()
![]()
Total revenue in I market= ₹46000
Total revenue in II market=₹53000
(b) The unit costs of ![]() and
and ![]() are ₹2.00 , ₹1.00 and 50 paise respectively.
are ₹2.00 , ₹1.00 and 50 paise respectively.
Consequently,
total cost price of each market:
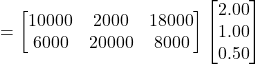
![]()
![]()
![]()
Profit: ![]()
![]()
Thus, the gross profit in market I is ₹ ![]() and in market II is ₹
and in market II is ₹ ![]() .
.
Question 11: Find the matrix![]() so that
so that ![]()
Solution: ![]()
The matrix given on the R.H.S. of the equation is a ![]()
matrix and the one given on the L.H.S.of the equation is a ![]() matrix.
matrix.
now, Let ![]()
Therefore,
![]()
![]()
Equating the corresponding elements of the two matrices,
we have:
![]()
![]()
Now,
solving ![]() and
and ![]()
we get ,
![]()
again solving
![]() and
and ![]()
We get,
![]()
Hence the required matrix ![]()
Question 12: If ![]() and
and ![]() are square matrices of the same order such that
are square matrices of the same order such that ![]() ,then prove by induction that
,then prove by induction that ![]() .Further prove that
.Further prove that ![]() for all
for all ![]()
Solution: Given ![]() and
and ![]() are square matrices of the same order such that
are square matrices of the same order such that ![]() .
.
To prove:![]()
For ![]() ,we have:
,we have:
![]() .
.
therefore, the result is true for ![]() .
.
Let the result is true for ![]()
![]()
Now, we prove that the result is true for ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the result is true for ![]() .
.
Now, we have to prove that![]() For all
For all ![]()
For ![]() , we have:
, we have:
![]()
Therefore, the result is true for ![]() .
.
Let the result be true for ![]() .
.
![]()
Now, we prove that the result is true for ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Therefore, the result is true for ![]() .
.
Question 13: If ![]() is such that
is such that ![]() then,
then,
(A)![]()
(B)![]()
(C)![]()
(D) ![]()
Solution: It is given that ![]()
Therefore,
![]()
![]()
![]()
![]()
Now,![]()
Hence,
![]()
On comparing the corresponding elements, we have:
![]()
![]()
![]()
Thus, the correct option is C.
Question 14: If the matrix ![]() is both symmetric and skew symmetric, then
is both symmetric and skew symmetric, then
(A) ![]() is a diagonal matrix
is a diagonal matrix
(B) ![]() is a zero matrix
is a zero matrix
(C)![]() is a square matrix
is a square matrix
(D) None of these
Solution: If the matrix ![]() is both symmetric and skew symmetric, then
is both symmetric and skew symmetric, then
![]() and
and ![]()
Hence,
![]()
![]()
![]()
![]()
Therefore, ![]() is a zero matrix.
is a zero matrix.
Thus, the correct option is B.
Question 15: If![]() is a square matrix such that
is a square matrix such that ![]() , then
, then ![]() is equal to
is equal to
(A)![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
Solution: It is given that ![]() is a square matrix such that
is a square matrix such that ![]() .
.
Now,
![]()
![]()
![]()
![]()
![]()
![]()
Thus, the correct option is ![]() .
.

