A line l passes through point (-1,3,-2) and is perpendicular

by

 Question:

A line l passes through point (-1,3,-2) and is perpendicular to both the lines \frac{x}{1}=\frac{y}{2}=\frac{z}{3} and \frac{x+2}{-3}=\frac{y-1}{2}=\frac{z+1}{5}. Find the vector equation of the line l. Hence, obtain its distance from origin.

Solution:

Point (-1, 3, -2)

Equation of lines

\frac{x}{1}=\frac{y}{2}=\frac{z}{3}--(i)

\frac{x+2}{-3}=\frac{y-1}{2}=\frac{z+1}{5}--(ii)

Let dr’s of the line l are (a, b, c)

Equation of line passes through the point (-1, 3, -2) is

\frac{x+1}{a}=\frac{y-3}{b}=\frac{z+2}{c}---(iii)

Eq (iii) is perpendicular to (i) and (ii)

Hence,

1a+2b+3c=0--(iv)

-3a+2b+5c=0--(v)

—————————-
Solving (iv) and (v) using cross multiplication method

\Rightarrow \frac{a}{10-6}=\frac{b}{-9-5}=\frac{c}{2-(-6)}

\frac{a}{4}=\frac{b}{-14}=\frac{c}{8}

\Rightarrow \frac{a}{2}=\frac{b}{-7}=\frac{c}{4}

Putting the value in (iii)

line l : \frac{x+1}{2}=\frac{y-3}{-7}=\frac{z+2}{4}

Eq of line in vector form

\vec{r}= (-1\hat{i}+3\hat{j}-2\hat{k})+\lamda(2\hat{i}-7\hat{j}+4\hat{k})

Distance of line l from origin

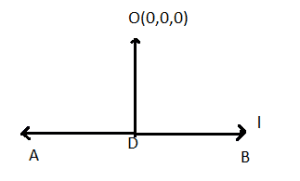
A line l passes through point (-1,3,-2) and is perpendicular

\frac{x+1}{2}=\frac{y-3}{-7}=\frac{z+2}{4}=k(Let)

\Rightarrow \frac{x+1}{2}=k,\frac{y-3}{-7}=k,\frac{z+2}{4}=k

\Rightarrow x =2k-1,y=-7k+3,z=4k-2

Point on the line l is D(2k-1,-7k+3, 4k-2)

Dr’s of line OD (2k-1-0,-7k+3-0, 4k-2-0)

=(2k-1,-7k+3, 4k-2)

Since OD is perpendicular line AB

Then 2(2k-1)-7(-7k+3)+ 4(4k-2)=0

\Rightarrow 4k-2+49k-21+16k-8=0

\Rightarrow 69k-31=0

\Rightarrow k = \frac{31}{69}=\frac{5}{33}

Hence point D[2(\frac{31}{69})-1,-7(\frac{31}{69})+3, 4(\frac{31}{69})-2]

\Rightarrow D[\frac{-7}{69},\frac{-10}{69},\frac{-14}{69}]

Distance from origin is OD

OD = \sqrt{(-\frac{7}{69}-0)^2+(-\frac{10}{69}-0)^2+(-\frac{14}{69}-0)^2}

=\sqrt{\frac{49}{(69)^2}+\frac{100}{(69)^2}+\frac{196}{(69)^2}}

=\sqrt{\frac{49+100+196}{(69)^2}}

=\sqrt{\frac{345}{(69)^2}}

=\sqrt{\frac{5}{69}}

Case study three dimension geometry 1
The equation of motion of a missile are x = 3t, y = -4t, z = t where the time

gmath.in

Leave a Comment