Case study chapter 12 (Linear programming)
Owner of a whole sale computer shop plans to sell two type of computers – a desktop and portable model that will cost ₹ 25000 and ₹ 40000 respectively.(Case study linear programming 1 chapter 12 class 12)

Based on the above information answer the question
(i) If the number of desktop model and portable model in the stock are x and y , to get maximum profit after selling and store of shop have capacity to keep computer not exceed 250 units, then which of the following is correct ?
(a) x + y = 250 (b) x + y > 250
(c) x + y ≥ 250 (d) x + y ≤ 250
(ii) If owner of shop does not want to invest more than ₹ 70 lakhs on both type of computer then which of the following is correct ?
(a) x + y ≤ 1000 (b) 5x + 8y ≥ 1400
(c) 5x + 8y ≤ 1400 (d) 5x + 8y = 1400
(iii) If the profit on the desktop model is ₹ 4500 and portable model is ₹ 5000, the profit Z is expressed as
(a) Z = 45x + 50y (b) Z = 4500x+5000y
(c) Z = 5000x+4500y (d) Z = x + y
(iv) The number of units of each type of computers which the owner of shop have in stock to get maximum profit is
(a) x = 250, y =100 (b) x = 100, y = 250
(c) x = 200, y = 100 (d) x = 200, y = 50
(v)The maximum profit is
(a) ₹ 11,25,000 (b) ₹11,15,000
(b) ₹ 11,80,000 (d) ₹11,50,000
Solution: (i) Answer (d)
From question total number of both type of computers will not be exceed 250.
x + y ≤ 250
(ii) Answer (c)
Maximum investment = ₹ 70 lakhs
Total cost of both type of computers = 25000 x + 40000 y
∴ 25000 x + 40000 y ≤ 70,00,000
⇒ 25 x + 40 y ≤ 7000
⇒ 5 x + 8 y ≤ 1400
(iii) Answer (b)
Profit on x desktop models = ₹ 4500 x
Profit on y portable models = ₹ 5000 y
Total profit (Z) = ₹ 4500 x + ₹ 5000 y
(iv) Answer (d)
We have p = 4500 x + 5000 y, which is to be maximise under constraint
x + y ≤ 250
5 x + 8 y ≤ 1400
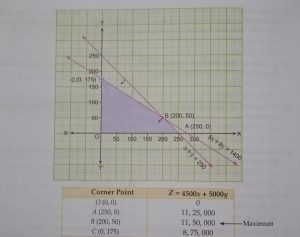
Also, OABC is a feasible region which is bounded.
The coordinates of corner points are O(0, 0), A(250, 0), B(200, 50), C(0, 175).
Now we evaluate at each corner point.
Corner point Z = 4500 x + 5000 y
O(0, 0) 0
A(250, 0) 11,25,000
B(200, 50) 11,50,000 ← maximum
C(0, 175) 8,75,000
For maximum profit
x( no. of desktop) = 200
y( no of portable) = 50
(v) Answer (d)
For x = 200, y = 50
Maximum profit Z is ₹ 11,50,000
Some Other Case study problem
Question: A dealer Ramprakash residing in a rural area open a shop to start his bussiness. He wishes to purchase a number of ceiling fans and table fans. A ceiling fan costs him ₹ 360 and table fan costs ₹ 240.
Based on the above information answer the question(Case study linear programming 2)

(i) If Ramprakash purchases x ceiling fans, y table fans. He has space in his store for at most 20 items, then which of the following is correct ?
(a) x + y = 20 (b) x + y > 20
(c) x + y < 20 (d) x + y ≤ 20
(ii) If Ramprakash has only ₹ 5760 to invest on both types of fan, then which of the following is correct ?
(a) x + y ≤ 5760 (b) 360 x + 240 y ≤ 5760
(c) 360 x + 240 y ≥ 5760 (d) 3 x + 2y ≤ 48
(iii) If he expects to sell ceiling fan at a profit of ₹ 22 and table fan for a profit of ₹ 18, then the profit is expressed as
(a) Z = 18x + 22y (b) Z = 22x + 18y
(c) Z = x + y (d) Z ≤ 22 x +18 y
(iv) If he sells all the fans that he buys, then the number x, y of both the type fans in stock to get maximum profit is
(a) x = 10, y = 12 (b) x = 12, y = 8
(c) x = 16, y = 0 (d) x = 8, y = 12
(v) The maximum profit after selling all fans
(a) ₹ 360 (b) ₹ 560
(c) ₹ 1000 (d) ₹ 392
Solution: For solution click here

